Оглавление:
Главная задача курса заключается в том, чтобы познакомить студентов с прикладными возможностями методов оптимизации, с тем, в каких случаях и какие методы следует применять для того или иного класса экстремальных задач, возникающих на разных этапах проектирования. Большое внимание уделяется вопросам постановки задачи и построения модели, подготовке к решению, выбору первого приближения к экстремальной точке, выбору стратегии оптимизации и т.д. В курсе рассматриваются только однокритериальные задачи, так как невозможно получить решение, которое, например, одновременно обеспечивает минимум затрат, максимум надежности и минимум потребляемой энергии. Преимущество отдается наиболее предпочтительному критерию, а остальные учитываются как ограничения задачи.
| Если что-то непонятно — вы всегда можете написать мне в WhatsApp и я вам помогу! |
Математическое программирование
Математическое программирование (МП) является одной из важнейших частей математической дисциплины «Математическое программирование» (МП).
Математическое программирование — это математическая дисциплина, посвященная теории и методам нахождения экстремумов функций многих переменных, при наличии дополнительных ограничений на эти переменные.
МП сформировалось в 50-х гг. 20 в. в связи с практическими задачами экономики (планирование и управление экономическими системами), техники (выбор наилучшего проекта или оптимальной конструкции), в военном деле и т.д. МП тесно связано с другим разделом математики — исследованием операций.
С каждой задачей МП связан критерий оптимальности, как правило это требование максимизировать или минимизировать одну или несколько числовых функций 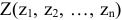 . В дальнейшем каждую функцию
. В дальнейшем каждую функцию 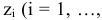
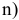 будем называть целевой функцией. В связи с тем, что любой реальный процесс, для которого ставится задача МП, имеет ограничения, они должны присутствовать и в его математической модели. Ограничения, как правило, это система, состоящая из уравнений и неравенств, которые задают некоторую область
будем называть целевой функцией. В связи с тем, что любой реальный процесс, для которого ставится задача МП, имеет ограничения, они должны присутствовать и в его математической модели. Ограничения, как правило, это система, состоящая из уравнений и неравенств, которые задают некоторую область 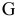 .
.
| Предмет математическое программирование |
Примеры задач математического программирования
Задача №1.1. (Задача планирования работы предприятия)
Предприятие может выпускать 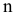 видов продукции. Прибыльность единицы продукции
видов продукции. Прибыльность единицы продукции 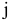 составляет
составляет 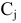 условных единиц. В производстве используется m видов ресурсов (сырье, рабочая сила, финансы и т.д.). Наличие
условных единиц. В производстве используется m видов ресурсов (сырье, рабочая сила, финансы и т.д.). Наличие 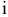 -го ресурса
-го ресурса 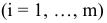 ограничено запасом
ограничено запасом 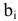 . Расход ресурса
. Расход ресурса 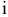 на производство изделия
на производство изделия 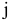 составляет
составляет 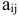 . Требуется определить план работы предприятия по объемам
. Требуется определить план работы предприятия по объемам  выпускаемой продукции таким образом, чтобы суммарная прибыль была максимальной.
выпускаемой продукции таким образом, чтобы суммарная прибыль была максимальной.
Составим математическую модель данной задачи. Целевая функция будет иметь вид
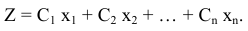
Область допустимых значений функции 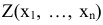 задается следующей системой неравенств
задается следующей системой неравенств
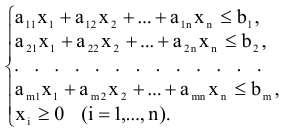
Требование к максимизации суммарной прибыли равносильно требованию к нахождению наибольшего значения функции 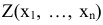 на области
на области 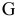 , задаваемой системой неравенств (1.2).
, задаваемой системой неравенств (1.2).
Задача №1.2. (Задача о диете)
Для нормальной жизнедеятельности человеку необходимо получать в день m различных питательных веществ (белки, углеводы, жиры, витамины и т.д.) в количествах 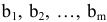 . Потребность в пище можно удовлетворить, используя
. Потребность в пище можно удовлетворить, используя 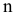 различных продуктов. Пусть единица
различных продуктов. Пусть единица 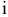 -го продукта стоит
-го продукта стоит 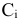 условных единиц и содержит
условных единиц и содержит 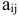 единиц питательного ингредиента
единиц питательного ингредиента 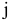 . Требуется составить суточный рацион питания, имеющий наименьшую стоимость.
. Требуется составить суточный рацион питания, имеющий наименьшую стоимость.
Задача о диете является одной из первых задач ИО.
Обозначим суточное потребление каждого продукта через  . Целевая функции, наименьшее значение которой необходимо найти, будет иметь вид
. Целевая функции, наименьшее значение которой необходимо найти, будет иметь вид
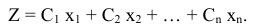
Решение допустимо, если соответствующий набор продуктов содержит питательных веществ не менее установленной нормы. Система ограничений имеет вид
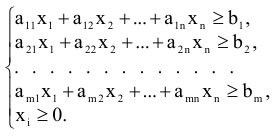
Задача №1.3. (Задача о рюкзаке)
Турист, отправляясь в поход, зашел в спортивный магазин. Для похода необходимо m предметов, причем 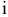 -тый предмет обладает объемом
-тый предмет обладает объемом 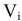 , массой
, массой 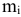 , ценой
, ценой 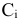 , и численной оценкой полезности
, и численной оценкой полезности 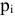 . Турист составляет набор из
. Турист составляет набор из 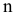 предметов (число
предметов (число 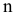 никак не фиксируется) так, чтобы суммарные затраты были минимальными, полезность — максимальной, в то же время объем предметов не должен превышать объема рюкзака
никак не фиксируется) так, чтобы суммарные затраты были минимальными, полезность — максимальной, в то же время объем предметов не должен превышать объема рюкзака 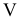 , а суммарная масса -массы
, а суммарная масса -массы 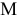 , которую турист в состоянии нести.
, которую турист в состоянии нести.
Присвоим вещам, которые составляют набор, номера 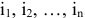 . В данном случае целевых функций две. Первая функция
. В данном случае целевых функций две. Первая функция
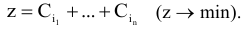
Вторая функция
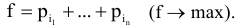
Ограничения имеют вид
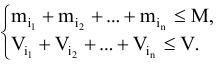
Данная задача имеет две целевые функции, т.е. является двукритериальной.
Особое место в МП занимает линейное программирование Линейное программирование (ЛП) — раздел исследований операций, задача которого состоит в отыскании экстремальных значений единственной целевой линейной функции на множестве, задаваемом системой линейных равенств или неравенств.
Примеры 1.1 и 1.2 являются типичными задачами ЛП. Пример 1.3 к задачам ЛП не относится. Подобные задачи выделяют в раздел многокритериальной оптимизации, которая в ряде аспектов смыкается с теорией игр.
Задачи ЛП являются математическими моделями многочисленных задач технико-экономического содержания. Основные результаты по решению задач ЛП были получены в 30-е — 40-е годы XX века. Развитие ЛП связано с именем американского ученого Дж. Данцига и советского математика и экономиста Леонида Витальевича Канторовича. Именно работа Канторовича 1939 года «Математические методы организации и планирования производства» сыграла основополагающую роль в развитии ЛП и в целом МП. За исследования в области экономики Л.В. Канторовичу в 1975 году была присуждена Нобелевская премия.
| Решение задач по математическому программированию |
Математические основы методов математического программирования
П.1. Базисные и опорные решения
Рассмотрим линейную систему из 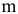 уравнений с
уравнений с 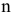 переменными
переменными
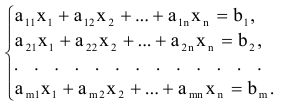
В дальнейшем будет интересен случай, когда 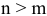 . Будем полагать, что в системе (2.1) все уравнения являются независимыми, что в свою очередь означает
. Будем полагать, что в системе (2.1) все уравнения являются независимыми, что в свою очередь означает 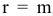 , где
, где 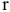 — ранг матрицы системы
— ранг матрицы системы 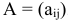 .
.
Рассмотрим одну из таких систем
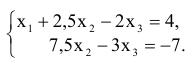
Составим расширенную матрицу системы и проведем несложные преобразования
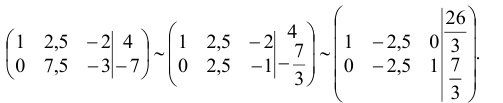
В данном случае 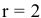 , число переменных
, число переменных 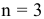 . Очевидно, что такая система имеет бесконечно много решений.
. Очевидно, что такая система имеет бесконечно много решений.
Перейдем от последней матрицы к системе уравнений
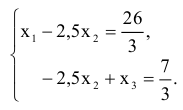
Выразим переменные 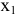 и
и 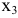 через переменную
через переменную 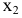
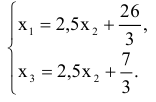
Рассмотрим столбцы перед переменными 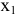 и
и 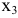 , как векторы
, как векторы 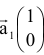 и
и 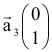 . Данные векторы образуют базис в двумерном пространстве. Отсюда название переменных
. Данные векторы образуют базис в двумерном пространстве. Отсюда название переменных 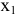 и
и 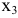 — базисные переменные.
— базисные переменные.
В общем случае базисных переменных в системе из 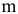 независимых уравнений с
независимых уравнений с 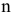 переменными будет
переменными будет 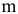 .
.
Определение 2.1. Базисными переменными системы 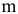 линейных уравнений с
линейных уравнений с 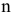 переменными
переменными 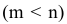 называется любой набор из
называется любой набор из 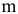 переменных, если определитель матрицы коэффициентов при них отличен от нуля.
переменных, если определитель матрицы коэффициентов при них отличен от нуля.
Оставшиеся  переменных называются свободными. В рассматриваемом примере свободной является переменная
переменных называются свободными. В рассматриваемом примере свободной является переменная 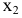 . Придавая переменной
. Придавая переменной 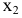 различные значения можно получить множество частных решений:
различные значения можно получить множество частных решений:
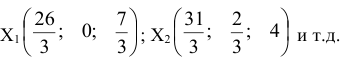
Решение 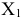 получается, если свободную переменную приравнять к нулю.
получается, если свободную переменную приравнять к нулю.
Определение 2.2. Если в общем решении системы m линейных уравнений с 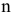 переменными (
переменными ( ) свободных переменных равны нулю, то такое решение называется базисным.
) свободных переменных равны нулю, то такое решение называется базисным.
Число базисных решений равно количеству неупорядоченных подмножеств из 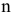 элементов (число неизвестных) по
элементов (число неизвестных) по 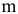 (число базисных неизвестных), т.е. это число равно
(число базисных неизвестных), т.е. это число равно
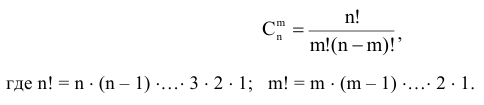
В данном примере число базисных решений определяется следующим образом
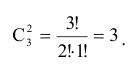
Среди базисных решений выделяют вырожденные решения, в которых нулевыми являются не только свободные решения, но и некоторые базисные.
Обратимся к примерам 1.1 и 1.2, рассмотренным в предыдущем параграфе. В системе ограничений одной и другой задачи присутствует требование неотрицательности переменных  . Это требование не является случайным, поскольку в экономических моделях, связанных с решением систем линейных уравнений, неизвестные величины соответствуют некоторым конкретным экономическим показателям, которые могут быть только неотрицательными. Неотрицательные базисные решения назовем опорными. Рассмотрим отыскание опорных решений на примере.
. Это требование не является случайным, поскольку в экономических моделях, связанных с решением систем линейных уравнений, неизвестные величины соответствуют некоторым конкретным экономическим показателям, которые могут быть только неотрицательными. Неотрицательные базисные решения назовем опорными. Рассмотрим отыскание опорных решений на примере.
| Примеры решения задач по математическому программированию |
Задача №2.1.
Найти все опорные решения системы линейных уравнений:
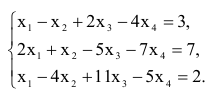
Решение:
Столбец свободных переменных не содержит отрицательных компонент. Если бы в каком-то уравнении были отрицательные свободные члены, нужно было бы умножением обеих частей уравнения на (- 1) сделать свободный член соответствующего уравнения положительным. Составим расширенную матрицу системы
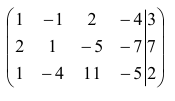
и определим первый разрешающий элемент так, чтобы в последнем столбце в результате элементарных преобразований не появились отрицательные компоненты. Очевидно, разрешающий элемент должен быть положительным. В первом столбце все компоненты положительные. Какой из них можно взять в качестве разрешающего? Составим отношения :
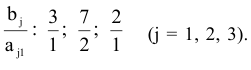
Если за разрешающий элемент выбрать тот из элементов первого столбца, которому соответствует минимальное отношение, то в столбце свободных членов после преобразований не будет отрицательных компонент — это элемент 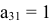 . Получим
. Получим
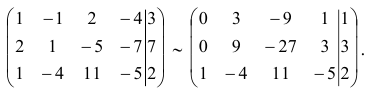
Во втором столбце первоначальной матрицы за разрешающий можно взять только элемент 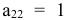 (он единственный положительный элемент этого столбца)
(он единственный положительный элемент этого столбца)
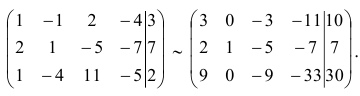
В третьем столбце за разрешающий можно взять 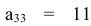 , т. к.
, т. к.
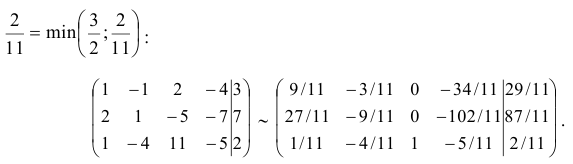
В четвертом столбце все элементы отрицательные и разрешающий элемент выбрать нельзя.
Остановимся на первом варианте и продолжим процесс далее
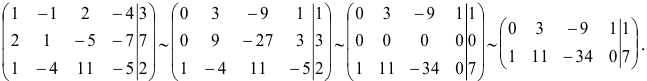
Очевидно, ранг матрицы равен 2, базисные неизвестные — 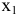 и
и 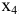 ; свободные —
; свободные — 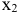 и
и 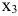 . Общее решение:
. Общее решение:
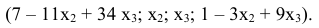
Базисное решение (7; 0; 0; 1) является опорным.
В данном случае существует
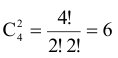
базисных решений, соответствующих базисным переменным:
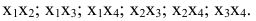
Вариант 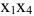 уже был рассмотрен.
уже был рассмотрен.
Вернемся к матрице системы, полученной после преобразований:
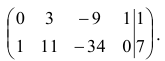
Варианты 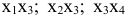 невозможны, т.к. в столбце, соответствующем
невозможны, т.к. в столбце, соответствующем 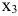 , нет положительных компонент, и
, нет положительных компонент, и 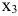 не может войти в базис. Введем в базис
не может войти в базис. Введем в базис 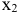 :
:
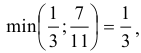
значит разрешающий элемент 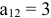 . Получим
. Получим
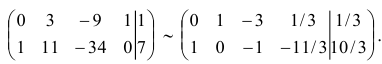
Базисное решение
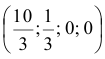
опорное.
Проверим последний вариант 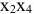 : в четвертом столбце последней матрицы разрешающим может быть только элемент
: в четвертом столбце последней матрицы разрешающим может быть только элемент 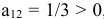 , но тогда из базиса уйдет неизвестная
, но тогда из базиса уйдет неизвестная 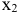 и получим базисные переменные
и получим базисные переменные 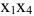 , что уже было рассмотрено.
, что уже было рассмотрено.
Итак, опорные решения: (7; 0; 0; 1) и
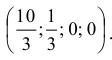
Сформулируем общее правило выбора разрешающего элемента при отыскании опорного решения для определенного столбца 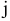 .
.
- Приводим систему уравнений к виду, когда в столбце свободных членов нет отрицательных чисел.
- В выбранном столбце
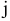 в «конкурсе» на звание «разрешающий элемент» участвуют только положительные элементы.
в «конкурсе» на звание «разрешающий элемент» участвуют только положительные элементы. - Каждый элемент в столбце свободных членов, делим на соответствующий ему элемент столбца
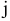 .
. - Выбираем из полученных соотношений наименьшее
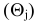 .
. - Элемент, для которого отношение, полученное в пункте 3, наименьшее, является разрешающим элементом.
П. 2. Свойства выпуклых множеств
Рассмотрим некоторые свойства выпуклых множеств.
Определение 23. Выпуклым множеством называется множество в векторном пространстве, которое вместе с любыми двумя точками множества содержит все точки соединяющего их отрезка.
Свойства выпуклых множеств.
1) Пересечение любой совокупности выпуклых множеств есть выпуклое множество.
Среди точек выпуклого множества выделяют внутренние и граничные точки.
Точка множества называется внутренней, если существует такая ее окрестность, в которой содержатся только точки данного множества.
Точка называется граничной точкой множества, если любая ее окрестность содержит как точки принадлежащие множеству, так и точки, не принадлежащие множеству. Множество граничных точек образует границу множества. Множество, содержащие свою границу, называется замкнутым.
Среди граничных точек важную роль в дальнейшем будут играть угловые точки.
2) Через каждую точку границы выпуклого множества на плоскости проходит по крайней мере одна опорная прямая, имеющая общую точку с границей, но не рассекающая это множество (на рис. 2.1 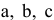 — опорные прямые).
— опорные прямые).
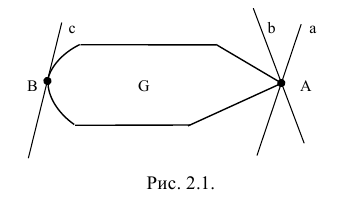
3) Замкнутое выпуклое множество есть пересечение конечного числа замкнутых полупространств.
Пересечение конечного числа замкнутых пространств назовем выпуклым многогранником.
Угловой точкой назовем точку множества, если она не является внутренней ни для какого отрезка, целиком принадлежащего данному множеству. Точки 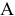 и
и 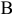 являются угловыми точками множества
являются угловыми точками множества 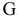 .
.
П. 3. Свойства решений задачи линейного программирования
Перед тем, как изложить основные свойства задачи ЛП, изложим основные формы записи общей задачи ЛП.
Прежде всего, отметим, что любую систему ограничений задачи ЛП можно привести к системе линейных уравнений. При этом суть самой задачи не изменится.
| Заказать работу по математическому программированию |
Рассмотрим следующую задачу
Задача №2.2.
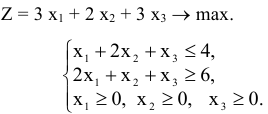
Поставим задачу — привести систему неравенств (*) к системе уравнений.
Для этого введем две дополнительные неотрицательные переменные 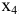 и
и 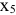 . В первом неравенстве для превращения его в равенство переменную добавим, во втором — вычтем. Получим
. В первом неравенстве для превращения его в равенство переменную добавим, во втором — вычтем. Получим
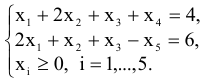
Будем считать, что новые переменные в целевой функции имеют коэффициенты 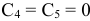 и не влияют на нее.
и не влияют на нее.
Любую систему ограничений, заданную неравенствами, можно перевести в систему уравнений, если в неравенствах со знаком 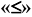 прибавить новую переменную, а в неравенствах со знаком
прибавить новую переменную, а в неравенствах со знаком 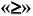 новую переменную отнять.
новую переменную отнять.
Задачу ЛП в этом случае можно сформулировать следующим образом:
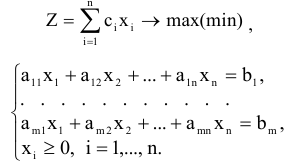
В матричном виде задачу ЛП можно записать следующим образом:
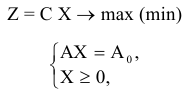
где
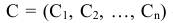
матрица строка,
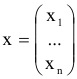
матрица столбец переменных
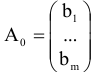
матрица столбец свободных членов,
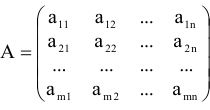
матрица системы.
Задачу ЛП можно записать в векторной форме следующим образом
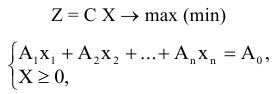
где 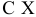 — скалярное произведение векторов
— скалярное произведение векторов
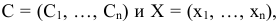
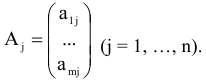
Сформулируем свойства задачи:
- Множество всех решений системы ограничений задачи ЛП является выпуклым.
- Если задача ЛП имеет оптимальное решение, то целевая функция принимает максимальное (минимальное) значение в одной угловой точке многогранника решений. Если целевая функция принимает максимальное (минимальное) значение в двух угловых точках многогранника решений, то она принимает оптимальное значение и в любой другой точке отрезка, соединяющего указанные точки.
- Каждому опорному значению задачи ЛП соответствует угловая точка многогранника и наоборот, каждой угловой точке многогранника соответствует опорное решение задачи ЛП.
Из свойств 1) — 3) следует, что оптимальное решение задачи ЛП, т.е. набор значений 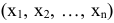 , следует искать только среди конечного числа опорных решений системы уравнений ограничений.
, следует искать только среди конечного числа опорных решений системы уравнений ограничений.
Казалось бы, алгоритм решения задачи ЛП готов. Следует найти все опорные решения и выбрать из них те, которым соответствует оптимальное значение целевой функции. На практике, как говорится, не все так просто.
| Помощь по математическому программированию |
Геометрический метод решения задач математического программирования
Цель данного параграфа — представить достаточно простой и наглядный способ решения задачи ЛП для случая, когда число независимых переменных не более трех — геометрический метод. На практике наиболее часто геометрический метод применяется в случае, когда переменных две. В дальнейшем ограничимся именно этим числом переменных.
Если число переменных 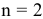 , целевая функция и система ограничений допускают следующую геометрическую интерпретацию. Целевая функция
, целевая функция и система ограничений допускают следующую геометрическую интерпретацию. Целевая функция
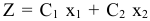
на координатной плоскости представляет собой семейство параллельных прямых. Неравенства вида
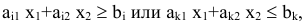
задают на плоскости полуплоскости, система ограничений задает выпуклый многоугольник.
Рассмотрим более подробно геометрическую интерпретацию целевой функции. При каждом фиксированном значении 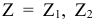 и т.д. целевая функция будет представлять собой прямую, перпендикулярную вектору
и т.д. целевая функция будет представлять собой прямую, перпендикулярную вектору 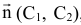 , заданную общим уравнением прямой (см. [1]). При
, заданную общим уравнением прямой (см. [1]). При 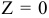 прямая
прямая 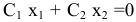 проходит через начало координат. При движении по направлению вектора
проходит через начало координат. При движении по направлению вектора 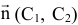 значение
значение 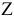 увеличивается, при движении в противоположную сторону — уменьшается.
увеличивается, при движении в противоположную сторону — уменьшается.
Рассмотрим применение геометрического метода на примерах.
Задача №3.1.
Для изготовления единицы сплава № 1 требуется металла 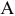 — 2 единицы, металла
— 2 единицы, металла 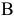 — 3 единицы и металла
— 3 единицы и металла 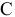 — 4 единицы. Для изготовления единицы сплава № 2 требуется 2, 5 и 2 единицы металлов
— 4 единицы. Для изготовления единицы сплава № 2 требуется 2, 5 и 2 единицы металлов 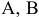 и с соответственно. Всего запасы металлов
и с соответственно. Всего запасы металлов 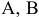 и с составляют соответственно 24, 50 и 40 единиц. Прибыль от реализации единицы сплава № 1 — 20 у.е., от реализации сплава № 2 — 30 у.е. Сколько единиц сплавов № 1 и № 2 нужно изготовить, чтобы суммарная прибыль была максимальной.
и с составляют соответственно 24, 50 и 40 единиц. Прибыль от реализации единицы сплава № 1 — 20 у.е., от реализации сплава № 2 — 30 у.е. Сколько единиц сплавов № 1 и № 2 нужно изготовить, чтобы суммарная прибыль была максимальной.
Решение:
Составим математическую модель задачи.
Пусть 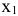 — число единиц сплава № 1,
— число единиц сплава № 1, 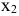 — число единиц сплава № 2.
— число единиц сплава № 2.
В этом случае прибыль от реализации сплавов № 1 и № 2 рассчитывается по формуле
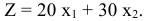
Система ограничений, которая обуславливается запасами металлов 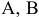 и
и 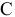 , будет иметь вид:
, будет иметь вид:
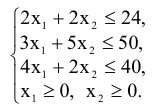
Требуется найти координаты вектора 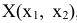 , при которых целевая функция
, при которых целевая функция 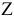 принимает максимальное значение.
принимает максимальное значение.
Замечание. Поясним, как получилась система ограничений на примере первого неравенства. Поскольку на единицу сплава № 1 затрачивается 2 единицы металла 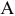 , то на изготовление
, то на изготовление 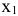 единиц сплава № 1 пойдет 2
единиц сплава № 1 пойдет 2 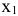 единиц металла
единиц металла 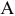 . Аналогично для изготовления
. Аналогично для изготовления 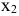 единиц сплава № 2 израсходуется 2
единиц сплава № 2 израсходуется 2 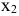 единиц металла
единиц металла 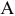 . суммарный расход металла
. суммарный расход металла 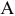 составит
составит 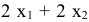 , который по условию задачи не должен превышать 24 единицы.
, который по условию задачи не должен превышать 24 единицы.
Построим область решений системы неравенств на координатной плоскости 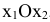 .
.
Это удобно сделать следующим образом:
- Записать уравнения, определяющие границу множества допустимых решений задачи ЛП,
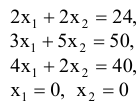
и построить их.
- Каждое из неравенств представляет собой полуплоскость, ограниченную соответствующей прямой (*). Чтобы выбрать нужную полуплоскость, можно взять любую точку, не принадлежащую прямой, если координаты точки удовлетворяют исходному неравенству, то сама точка находится в нужной полуплоскости, в противном случае нужно взять другую полуплоскость.
Например, если подставить в неравенство 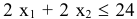 координаты точки
координаты точки 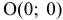 , то получим верное неравенство
, то получим верное неравенство 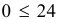 . Поэтому следует выбрать полуплоскость, изображенную на рисунке 3.1.
. Поэтому следует выбрать полуплоскость, изображенную на рисунке 3.1.
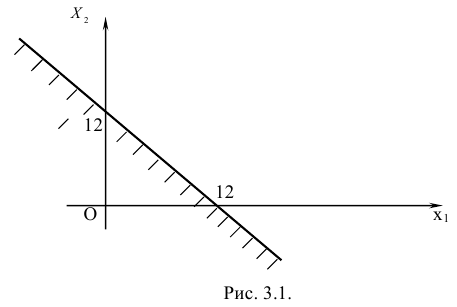
Действуя аналогично, изобразим множество допустимых решений задачи (рис. 3.2).
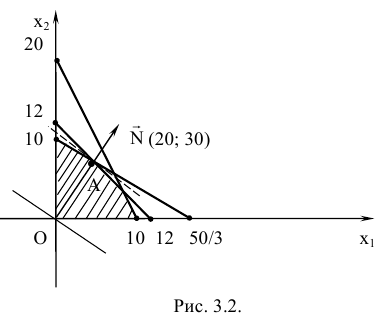
Построим опорную прямую 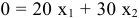 . данная прямая перпендикулярна вектору
. данная прямая перпендикулярна вектору 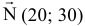 .
.
При перемещении опорной прямой перпендикулярно вектору 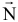 по его направлению значение целевой функции возрастает. Следовательно, свое максимальное значение целевая функция принимает в точке множества допустимых решений наиболее удаленной от прямой
по его направлению значение целевой функции возрастает. Следовательно, свое максимальное значение целевая функция принимает в точке множества допустимых решений наиболее удаленной от прямой 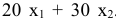 В данном случае эта точка —
В данном случае эта точка — 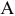 , которая получается при пересечении прямых
, которая получается при пересечении прямых
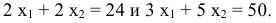
Координаты точки 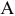 найдем, решив систему уравнений
найдем, решив систему уравнений
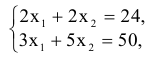
получим
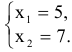
Найдем максимальное значение целевой функции
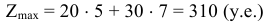
| Задача линейного программирования |
Задача №3.2.
Для кормления скота используются грубые корма и концентраты. В 1 кг концентратов содержится 0,8 кормовых единиц и 0,06 кг протеина, в 1 кг грубых кормов содержится 0,3 кормовых единиц и 0,05 кг протеина. Суточный рацион должен содержать не менее 12 кормовых единиц и не менее 1,5 кг протеина. Необходимо составить дневной рацион, имеющий минимальную стоимость, если 1 кг концентрата стоит 10 у.е., а 1 кг грубых кормов — 6 у.е.
Решение:
Данная задача является частным случаем задачи о составлении диеты (см. пример 1.2).
Обозначим через 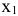 — суточное потребление в кг концентратов,
— суточное потребление в кг концентратов, 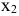 — суточное потребление в кг грубых кормов. Тогда целевая функция примет вид:
— суточное потребление в кг грубых кормов. Тогда целевая функция примет вид:
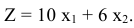
Система ограничений —
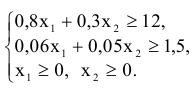
Аналогично тому, как это делалось в примере 3.1, изобразим на координатной плоскости 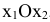 область, соответствующую системе ограничений и опорную прямую
область, соответствующую системе ограничений и опорную прямую 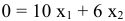 (рис. 3.3).
(рис. 3.3).
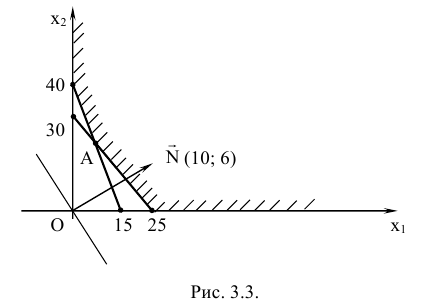
В данном случае по условию задачи требуется определить план 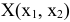 , при котором значение целевой функции наименьшее. На графике
, при котором значение целевой функции наименьшее. На графике 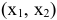 — это координаты точки множества допустимых решений, находящейся ближе к опорной прямой. Искомая точка — точка
— это координаты точки множества допустимых решений, находящейся ближе к опорной прямой. Искомая точка — точка 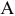 . Определим ее координаты. Как решение системы уравнений
. Определим ее координаты. Как решение системы уравнений
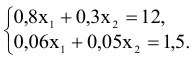
Получим
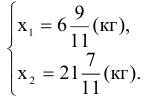
Наименьшее значение целевой функции
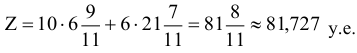
Как можно было убедиться на разобранных примерах, геометрический способ решения задач ЛП достаточно удобен. Однако данный метод не является универсальным. Самым главным его недостатком является то, что его можно применять в том случае, когда число переменных в стандартной задаче ЛП равно двум. Так же геометрический метод не всегда дает точный результат.
Замечание 3.1. Геометрический метод ЛП можно применить и в том случае, когда система ограничений содержит 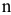 неизвестных и
неизвестных и 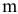 линейно независимых условий, причем
линейно независимых условий, причем 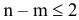 .
.
Симплексный метод решения задачи математического программирования
П.1. Геометрическая интерпретация симплексного метода
В данном параграфе будет предложен достаточно общий метод решения задач ЛП. Прежде, чем изложить его теоретические основы, рассмотри те трудности, с которыми придется «сражаться» общему методу решения задач ЛП.
Во-первых, согласно свойствам решений задачи ЛП оптимальное решение совпадает с одним из опорных решений системы ограничений. Если число переменных 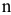 , число уравнений системы ограничений
, число уравнений системы ограничений 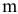 . То верхня граница числа опорных решении
. То верхня граница числа опорных решении
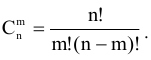
При достаточно больших 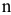 число опорных решений становится столь велико, что никакая самая мощная ЭВМ не справится с задачей простого перебора опорных решений. Поэтому необходимо научиться отбрасывать заведомо плохие решения и работать только с перспективными.
число опорных решений становится столь велико, что никакая самая мощная ЭВМ не справится с задачей простого перебора опорных решений. Поэтому необходимо научиться отбрасывать заведомо плохие решения и работать только с перспективными.
Нечто подобное мы проделывали при работе с геометрическим методом (см. рис. 4.1).
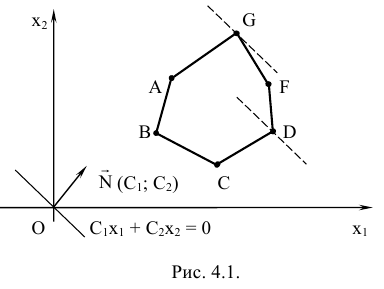
При геометрическом методе опорная прямая перемещается в ту угловую точку многогранника, которой соответствует оптимальное значение функции. Для минимума это первая точка множества допустимых решений, встретившаяся на пути целевой функции при движении ее по вектору 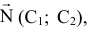 для максимума — последняя. Такую операцию можно проделать потому, что мы видим на плоскости и множество допустимых значений и опорную прямую. В случае
для максимума — последняя. Такую операцию можно проделать потому, что мы видим на плоскости и множество допустимых значений и опорную прямую. В случае 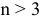 приходится действовать вслепую.
приходится действовать вслепую.
Представим себе такую ситуацию. На полу изображен рисунок 4.1. Вместо угловых точек находятся выпуклые отметки, на которых выбиты координаты данных точек. Человек с завязанными глазами обладает достаточно чувствительными пальцами, чтобы нащупать отметку и определить числа, выбитые на ней. Полученные координаты он подставляет в целевую функцию. Будем считать, что основная трудность состоит в том, чтобы определить координаты точки.
Если на этом возможности человека заканчиваются, то ему остается только переходить от точки к точке, проводя каждый раз достаточно трудоемкий процесс подсчета. При этом он не знает, в каком месте многоугольника он находится. Предположим, что он сразу наткнулся на точку 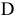 . В этом случае его путь будет таким:
. В этом случае его путь будет таким:
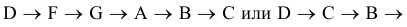
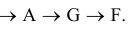
Это соответствует простому перебору опорных решений. Что невозможно по техническим причинам.
Дадим бедняге подсказку. Пусть каждая угловая точка имеет свою температуру. Причем, чем дальше точка находится от прямой
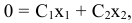
тем она горячее. Теперь человек с завязанными глазами может действовать следующим образом. Он определит разницу температур между точкой, где он находится, и соседними точками. Если разница положительна, то данная точка есть точка максимума целевой функции. Если есть отрицательные разницы температур, то точка не является искомой, и человеку надо переместиться в соседнюю точку, более горячую. Если таких точек несколько, то следует выбрать самую горячую. В этом случае перебор опорных решений будет целенаправленный. Заведомо «плохие» угловые точки рассматриваться не будут. Поэтому путь из точки  в точку максимума
в точку максимума 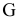 будет таким:
будет таким: 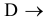
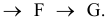 Выходит, что такая «температурная» подсказка значительно упрощает решение задачи ЛП.
Выходит, что такая «температурная» подсказка значительно упрощает решение задачи ЛП.
Теперь можно сформулировать три основных элемента общего метода решения задачи ЛП.
- Способ определения какого-либо первоначального опорного решения задачи ЛП (рассмотрен в § 2).
- Критерий проверки оптимальности решения.
- Правило перехода к лучшему (в общем случае не к худшему) решению.
Замечание 4.1. Добавление «не к худшему» связано с тем, что иногда переход от одного плана к другому не дает моментального выигрыша, но в дальнейшем оказывается весьма полезным.
Все три необходимых элемента содержит симплексный метод (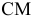 ) (лат. simplex — простой).
) (лат. simplex — простой).
Еще раз сформулируем суть 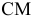 .
.
Симплексный метод — это метод последовательного улучшения решений задачи Л П.
П. 2. Математические основы симплексного метода
Пусть задача ЛП задана в канонической форме. Для определенности будем рассматривать задачу на нахождение максимума линейной функции. Запишем задачу ЛП в векторной форме:
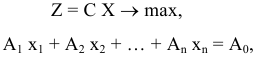
где
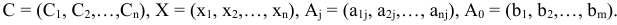
Предположим, что согласно правилу, сформулированному в § 2, найдено некоторое первоначальное решение задачи ЛП
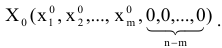
Замечание 4.2. Предполагается, что базисными будут первые m переменных, что не влияет на общность рассуждений, поскольку переменные всегда можно перенумеровать.
Условие (4.1) можно переписать следующим образом:
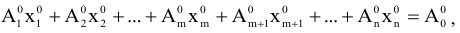
где
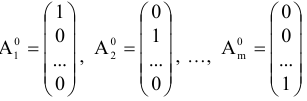
линейно независимые единичные векторы 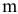 -мерного векторного пространства. Они образуют базис данного пространства.
-мерного векторного пространства. Они образуют базис данного пространства.
Поскольку разложение вектора по базису единственно, получим, что для вектора 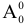 и любого вектора
и любого вектора 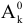 , не входящего в базис, справедливо следующее однозначное представление:
, не входящего в базис, справедливо следующее однозначное представление:
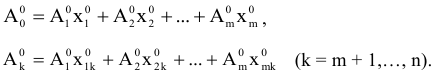
Каждому из векторов можно поставить в соответствие значение
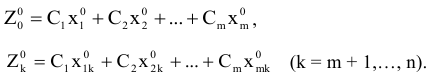
Сформулируем главное утверждение данного раздела.
Теорема 4.1. (Теорема об оптимальности плана) Если для некоторого вектора 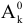 выполняется условие
выполняется условие
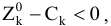
то план
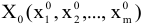
не является оптимальным и можно построить такой план 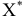 для которого выполняется условие
для которого выполняется условие 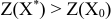 .
.
Доказательство. Зададим некоторое число 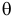 > 0. Умножим уравнение (4.3) на
> 0. Умножим уравнение (4.3) на 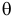 и вычтем из уравнения (4.2). Получим
и вычтем из уравнения (4.2). Получим
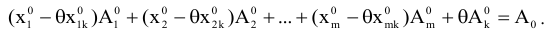
Поскольку значения 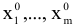 положительны, то всегда можно подобрать такие значения 9, чтобы координаты
положительны, то всегда можно подобрать такие значения 9, чтобы координаты 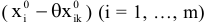 были неотрицательны. (Точнее все значения, кроме одного, будут положительны. Одно значение будет равно нулю, и соответствующий ему вектор выйдет из базиса.) Выражение (4.6) представляет собой разложение вектора
были неотрицательны. (Точнее все значения, кроме одного, будут положительны. Одно значение будет равно нулю, и соответствующий ему вектор выйдет из базиса.) Выражение (4.6) представляет собой разложение вектора 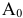 по новому базису. Таким образом, получен новый опорный план
по новому базису. Таким образом, получен новый опорный план
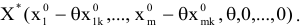
Значение целевой функции, соответствующей новому опорному плану, найдем по формуле
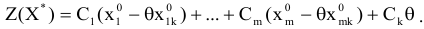
Для того, чтобы выяснить, как изменилась целевая функция, проведем следующие преобразования:
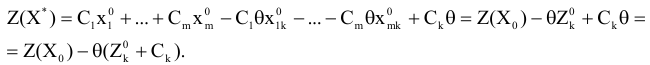
По предположению
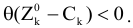
Значит
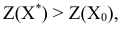
Что и требовалось доказать.
Из результатов теоремы 4.1 несложно получить утверждение. Следствие 4.1. Если для некоторого плана 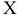 разложение всех векторов
разложение всех векторов 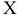 в данном базисе удовлетворяют условию
в данном базисе удовлетворяют условию
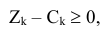
то план 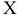 является оптимальным.
является оптимальным.
Действительно, как было показано при доказательстве теоремы 4.1 при изменении базиса в задаче ЛП, целевая функция изменяется на величину — 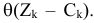 . Следовательно, при неотрицательных
. Следовательно, при неотрицательных  план
план 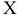 улучшить нельзя.
улучшить нельзя.
Теорема 4.2. Пусть для задачи ЛП
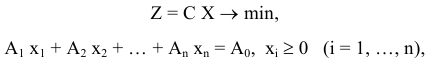
Найден некоторый первоначальный план 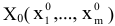 , тогда, если для некоторого вектора
, тогда, если для некоторого вектора 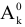 выполняется условие
выполняется условие 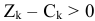 , то план не является оптимальным. Можно построить такой план
, то план не является оптимальным. Можно построить такой план 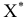 , для которого будет выполняться условие
, для которого будет выполняться условие 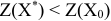 .
.
Следствие 4.2. Если для некоторого плана 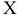 разложения всех векторов
разложения всех векторов 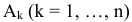 в данном базисе удовлетворяют условию
в данном базисе удовлетворяют условию
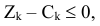
то план 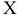 является оптимальным.
является оптимальным.
Доказательство данных утверждений рекомендуется провести самостоятельно.
Приведенные теоремы и их сведения составляют теоретическую основу симплексного метода.
С их помощью можно сформировать три основных этапа симплексного метода.
- находится любое опорное решение (базис m-мерного пространства) системы уравнений, соответствующих ограничениям задачи ЛП.
- Для того, чтобы проверить полученный план на оптимальность, необходимо для каждого вектора
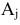 определить значение
определить значение 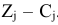 В дальнейшем значение
В дальнейшем значение 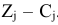 будем называть оценкой вектора
будем называть оценкой вектора 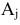 . Если в задаче на максимум среди оценок есть отрицательные, то данный опорный план не оптимальный. В задаче на минимум на оптимальность плана указывают положительные оценки.
. Если в задаче на максимум среди оценок есть отрицательные, то данный опорный план не оптимальный. В задаче на минимум на оптимальность плана указывают положительные оценки. - В случае, если план не оптимальный, согласно результатам теоремы 4.1 и теоремы 4.2, нужно ввести в базис вектор
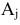 , оценка которого нас не устраивает. При этом целевая функция улучшится на величину
, оценка которого нас не устраивает. При этом целевая функция улучшится на величину 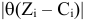 . То есть она увеличится в задаче на максимум или уменьшится в задаче на минимум. Если имеется несколько векторов с «плохими» оценками, то для введения в базис выбирается тот, для которого соответствующее значение
. То есть она увеличится в задаче на максимум или уменьшится в задаче на минимум. Если имеется несколько векторов с «плохими» оценками, то для введения в базис выбирается тот, для которого соответствующее значение 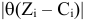 наибольшее.
наибольшее.
| Решение задач по линейному программированию |
П. 3. Примеры
Рассмотрим работу симплексного метода на примерах.
Задача №4.1.
Найти максимальное значение целевой функции
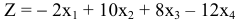
При ограничениях
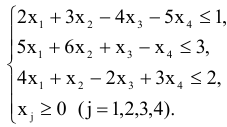
Решение:
Приведем систему ограничений к каноническому виду. Поскольку в системе ограничений все неравенства 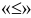 , то дополнительные переменные прибавляются.
, то дополнительные переменные прибавляются.
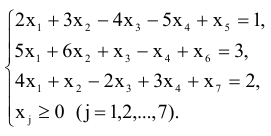
На данный момент существует достаточно много методических приемов использования 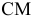 для решения задач ЛП. На наш взгляд для расчетов с использованием бумаги и ручки (и головы) удобно использовать симплексные таблицы. Они избавляют от утомительного переписывания уравнений, упорядочивают вычисления и служат своего рода органайзером. Напомним, какие действия нужно совершить и в какой последовательности.
для решения задач ЛП. На наш взгляд для расчетов с использованием бумаги и ручки (и головы) удобно использовать симплексные таблицы. Они избавляют от утомительного переписывания уравнений, упорядочивают вычисления и служат своего рода органайзером. Напомним, какие действия нужно совершить и в какой последовательности.
Составим симплексную таблицу.
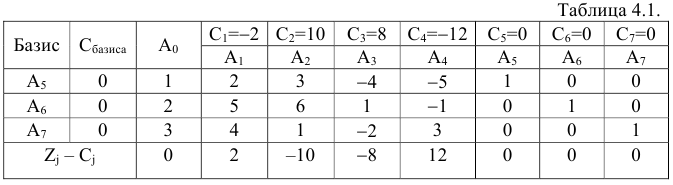
Поясним устройство симплексной таблицы.
Первый столбец таблицы содержит наименование векторов, которые на данной итерации являются базисными.
Векторы в базис должны записываться в определенном порядке. Каждый вектор находится в той же строке, что единица в единичном столбике этого вектора. Например, вектор 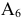 базисный. Он записывается во второй строке, поскольку единица в столбце
базисный. Он записывается во второй строке, поскольку единица в столбце 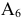 находится во второй строке.
находится во второй строке.
Во втором столбце записывается для базисного вектора 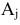 соответствующее значение из целевой функции.
соответствующее значение из целевой функции.
Третий столбец 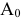 — это столбец свободных членов.
— это столбец свободных членов.
Последующие столбцы — это координаты векторов 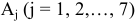 .
.
Над столбцами  подставлены для удобства
подставлены для удобства  . В строке
. В строке 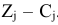 происходит оценка плана на оптимальность. С ее помощью выбирается очередной вектор для введения в базис.
происходит оценка плана на оптимальность. С ее помощью выбирается очередной вектор для введения в базис.
Итак, начнем решение задачи. В данном случае векторы 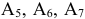 добавленных переменных
добавленных переменных 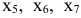 образуют базис трехмерного векторного пространства. Таким образом первоначальный опорный план
образуют базис трехмерного векторного пространства. Таким образом первоначальный опорный план 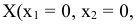
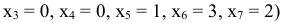 получился, можно сказать, автоматически.
получился, можно сказать, автоматически.
Проверим его на оптимальность. Для этого нужно заполнить строку 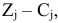 используя формулы
используя формулы
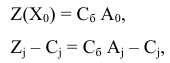
где 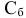 — вектор, составленный из коэффициентов целевой функции векторов, находящихся в базисе. В нашем случае
— вектор, составленный из коэффициентов целевой функции векторов, находящихся в базисе. В нашем случае 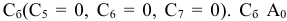 и
и 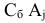 — скалярные произведения соответствующих векторов. Получим:
— скалярные произведения соответствующих векторов. Получим:

Обратите внимание, что в строке 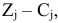 базисным векторам обязаны соответствовать нулевые оценки. Если это не так, ищите ошибку. Вы неправильно заполнили столбцы «Базис» и
базисным векторам обязаны соответствовать нулевые оценки. Если это не так, ищите ошибку. Вы неправильно заполнили столбцы «Базис» и 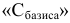 .
.
Первоначальный опорный план не является оптимальным, поскольку оценки векторов 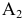 и
и 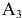 отрицательны. Согласно теореме 4.1, чтобы улучшить план нужно ввести в базис вектора, имеющие отрицательные оценки. В данной задаче таких векторов два. Из них нужно выбрать один, который при введении в базис дает наибольшую прибыль.
отрицательны. Согласно теореме 4.1, чтобы улучшить план нужно ввести в базис вектора, имеющие отрицательные оценки. В данной задаче таких векторов два. Из них нужно выбрать один, который при введении в базис дает наибольшую прибыль.
Рассмотрим вектор
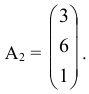
Найдем отношения координат вектора 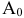 к соответствующим координатам вектора
к соответствующим координатам вектора 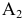 и выберем из соотношений наименьшее.
и выберем из соотношений наименьшее.
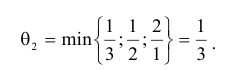
Найдем прибыль, которая будет получена от введения вектора 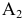 в базис
в базис
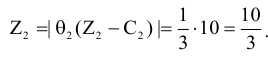
Рассмотрим вектор 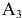 . Проведем для него аналогичные вычисления.
. Проведем для него аналогичные вычисления.
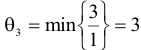
(две оставшихся координаты вектора отрицательны).
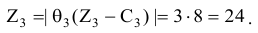
Поскольку 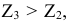 то введение в базис вектора
то введение в базис вектора 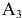 принесет большую выгоду. Таким образом, на следующем шаге решения в базис вводится вектор
принесет большую выгоду. Таким образом, на следующем шаге решения в базис вводится вектор 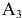 , причем разрешающим элементом является координата 1 (она выделена в таблице). Заметим, что в той же строке, где находится разрешающий элемент, стоит единица базисного вектора
, причем разрешающим элементом является координата 1 (она выделена в таблице). Заметим, что в той же строке, где находится разрешающий элемент, стоит единица базисного вектора 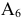 . Именно этому вектору суждено «проститься» с базисом. Составим вторую симплексную таблицу.
. Именно этому вектору суждено «проститься» с базисом. Составим вторую симплексную таблицу.
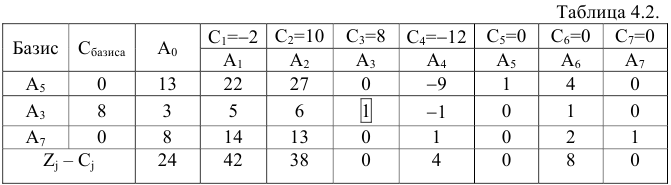
При составлении таблицы 4.2 были проведены следующие преобразования.
- Вторая строка осталась неизменной, поскольку разрешающий элемент равен единице, что и требуется.
- К первой строке прибавляется вторая, умноженная на четыре (1+ 411).
- К третьей строке прибавляется вторая, умноженная на два (III + 211).
Оценим план
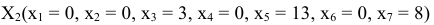
на оптимальность.
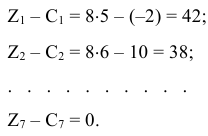
Поскольку среди полученных оценок нет отрицательных, то план 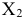 является оптимальным. Максимальное значение целевой функции находится в клетке
является оптимальным. Максимальное значение целевой функции находится в клетке
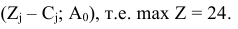
Заметим, что при итерации мы получим прибыль 24, на которую и рассчитывали. Если при решении задачи рассчитанное при выборе разрешающего элемента значение 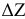 не совпадает с полученным в таблице, вы ошиблись в расчетах.
не совпадает с полученным в таблице, вы ошиблись в расчетах.
Задача №4.2.
Минимизировать функцию
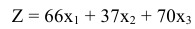
при ограничениях
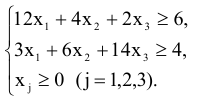
Решение:
Приведем задачу к каноническому виду
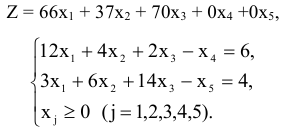
Составим симплексную таблицу
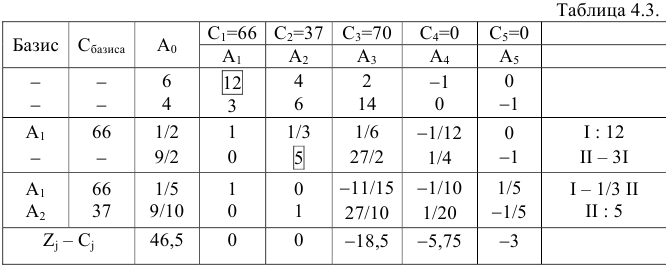
Дадим необходимые пояснения.
Во-первых, в отличие от примера 4.1 в данном случае первоначального опорного плане не было. Поэтому надо получить первоначальный опорный план. Векторы выбирались наугад, поскольку не было возможности оценить выгоду от введения того или иного вектора в базис. Случайно для базиса 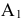 ,
, 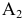 не оказалось положительных оценок, т.е. план
не оказалось положительных оценок, т.е. план 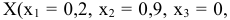
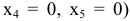 является оптимальным. Соответствующее значение целевой функции
является оптимальным. Соответствующее значение целевой функции
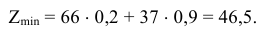
П. 4. Метод искусственного базиса
В примере 4.2 нам пришлось выбрать вектор наугад. Благодаря некоторому везению автора первый «попавшийся под руку» опорный план оказался
оптимальным. Однако всего для данной задачи можно было составить 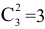 опорных плана, из которых два были бы неудачными. Конечного гораздо комфортнее решать задачу, когда первоначальный опорный план уже задан, как в примере 4.1. Для того, чтобы в общем случае задачи ЛП сразу получить набор базисных векторов существует метод искусственного базиса. Рассмотрим общую задачу ЛП,
опорных плана, из которых два были бы неудачными. Конечного гораздо комфортнее решать задачу, когда первоначальный опорный план уже задан, как в примере 4.1. Для того, чтобы в общем случае задачи ЛП сразу получить набор базисных векторов существует метод искусственного базиса. Рассмотрим общую задачу ЛП,
Требуется найти минимальное (максимальное) значение линейной функции
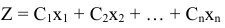
при ограничениях
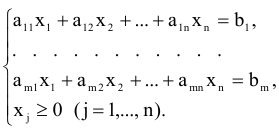
Предположим, что система ограничений не содержит единичной матрицы.
Составим расширенную задачу. Для этого в каждом уравнении в левой части добавим новую переменную. В целевую функцию новые переменные войдут с коэффициентом М, который предполагается достаточно большим для задачи на минимум и достаточно малым для задачи на максимум. Переменные, введенные указанным способом, назовем искусственными. Преобразуем исходную задачу ЛП.
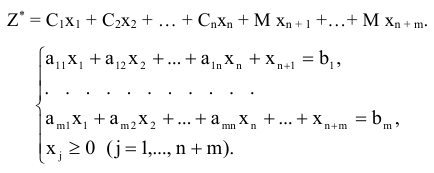
Справедливо следующее утверждение.
Теорема 4.3. Если в оптимальном плане
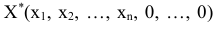
расширенной задачи искусственные переменные равны нулю, то план
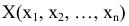
является оптимальным планом исходной задачи.
Рассмотрим работу метода искусственного базиса на примере.
| Методы решения задач линейного программирования |
Задача №4.3.
Найти минимальное значение линейной функции
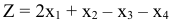
при ограничениях
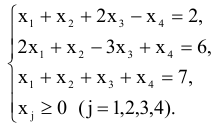
Решение:
Так как в системе ограничений нет единичного базиса, составим расширенную задачу.
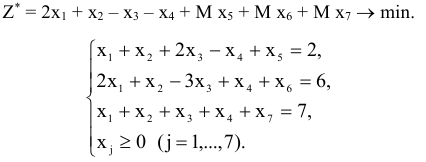
Составим симплексную таблицу. Теперь, опять таки, для удобства вычислений добавим еще одну оценочную строку 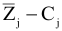 . По этой строке будем определять вектор, подлежащий включению в базис. Предстоит решить две задачи:
. По этой строке будем определять вектор, подлежащий включению в базис. Предстоит решить две задачи:
1) исключить из базиса все искусственные векторы;
2) отыскать (в случае необходимости) оптимальное решение задачи.
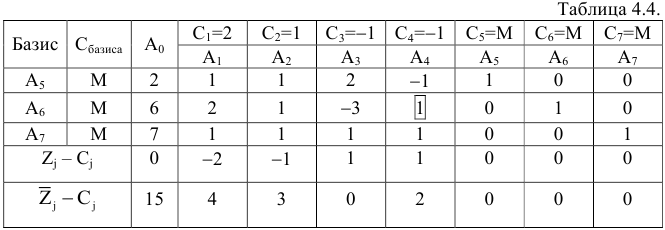
В данном случае в строке 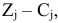 записываются оценки векторов при условии, что
записываются оценки векторов при условии, что 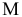 = 0. В строке
= 0. В строке 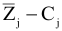 , записываются только коэффициенты перед
, записываются только коэффициенты перед 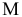 , т.е.
, т.е.
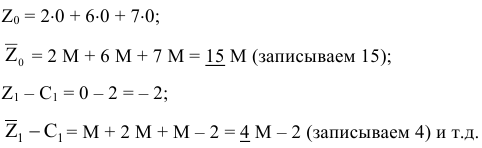
В строке 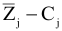 имеются положительные оценки (векторы
имеются положительные оценки (векторы 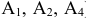 ), поэтому опорный план
), поэтому опорный план 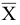 расширенной задачи не является оптимальным. Вычислим максимальное значение
расширенной задачи не является оптимальным. Вычислим максимальное значение 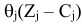 для первой итерации
для первой итерации
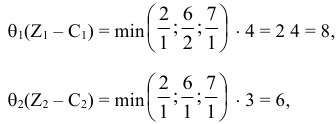
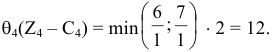
Наибольшую выгоду принесет введение в базис вектора 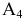 . При этом вектор
. При этом вектор 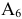 покинет базис.
покинет базис.
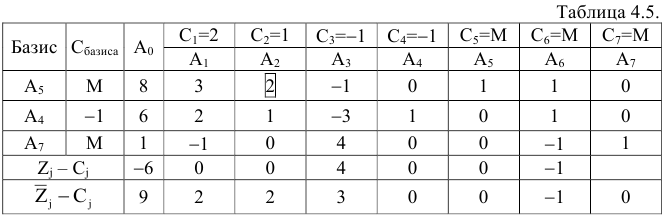
Проведем еще одну итерацию. Т. к. векторы 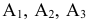 имеют положительные оценки
имеют положительные оценки 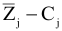
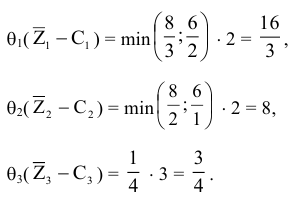
Выгоднее всего ввести в базис вектор 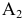 .
.
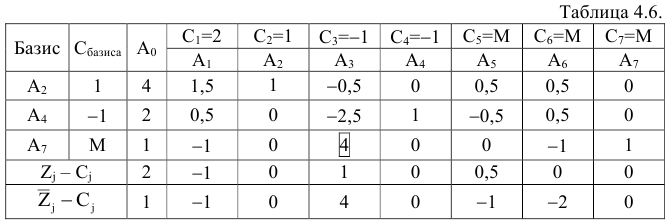
План 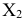 не является оптимальным, поскольку
не является оптимальным, поскольку 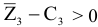 .
.
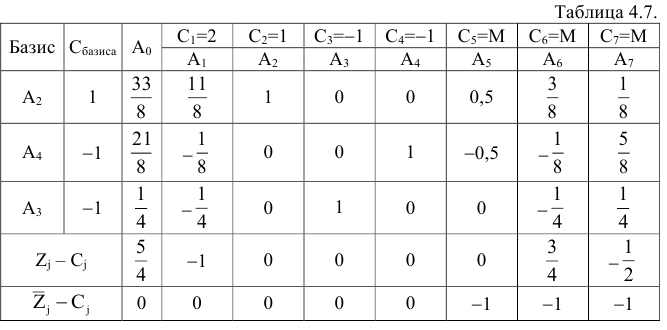
В таблице 4.7 в строке 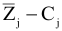 оценки всех векторов, кроме искусственных равны нулю, таким образом, исключены из базиса все искусственные векторы.
оценки всех векторов, кроме искусственных равны нулю, таким образом, исключены из базиса все искусственные векторы.
Оценим теперь план
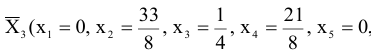
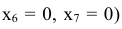
расширенной задачи на оптимальность, для этого объединим строки 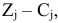 и
и 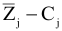 в одну.
в одну.

Было указано, что коэффициент 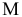 в задачах на минимум берется достаточно большим. Теперь можно указать границы, в которых находится
в задачах на минимум берется достаточно большим. Теперь можно указать границы, в которых находится 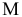 .
.
Таким образом, план 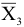 является оптимальным планом расширенной задачи. Следовательно, согласно теореме 4.3 план
является оптимальным планом расширенной задачи. Следовательно, согласно теореме 4.3 план
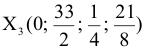
является оптимальным планом исходной задачи. При этом
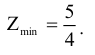
В заключение пункта приведем еще одно утверждение.
Теорема 4.4. Исходная задача ЛП не имеет решения, если расширенная задача не имеет решения или если оптимальное значение расширенной задачи соответствует плану, в котором в качестве базисных присутствуют искусственные переменные.
П. 5. Одна из важнейших математических проблем XXI века
В конце девяностых годов XX века выдающийся отечественный математик В.И. Арнольд от имени Международного математического союза написал ряду ведущих математиков мира, предложив им охарактеризовать некоторые проблемы математики в следующем XXI столетии. Сделать это предложение Арнольда вдохновил знаменитый список проблем Гильберта 1900 г.* В ответ на это предложение американский математик Стивен Смейл член национальной АН США выступил в 1997 г. с лекцией по случаю 60-летия Арнольда в Филдсовском институте (Торонто). В ней он сформулировал 18 проблем, которые отбирались по следующим критериям:
1) простая математически точна формулировка;
2) личное знакомство С. Смейла с задачей (широта интересов ученого дает возможность предположить, что практически невозможно найти вопрос в математике, с которым Смейл не знаком);
3) вера в то, что проблема, ее решение, частные результаты или даже попытки ее решить будут иметь важное значение для математики и ее развития в следующем столетии.
Девятой проблемой С. Смейл поставил проблему линейного программирования, которая сформулирована следующим образом.
Существует ли полиномиальный по времени алгоритм над множеством вещественных чисел, который определяет возможность решения линейной системы неравенства 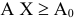 ?
?
Очевидно, что один из вариантов решения этой задачи связан с ее рассмотрением как задачи оптимизации линейного программирования: решить, существует ли 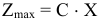 при ограничениях
при ограничениях 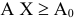 .
.
Изложенный в данном разделе симплексный метод в наихудшем варианте является экспоненциально медленным, т.е. сложность решения задачи ЛП возрастает значительно быстрее, чем числа п и т, определяющие условие задачи. С другой стороны есть все предпосылки надеяться, что существует более быстрый алгоритм решения задачи ЛП. Интересные результаты были получены Хачиным (метод эллипсоидов), Кармакером (метод внутренней точки)и др.
Действительно, как ни хорош симплексный метод, но он уступает геометрическому, поскольку все же действует «в слепую». Может быть, вскоре найдется человек, который сможет предложить метод решения задачи ЛП с «глазами»?
| Графическое решение задач линейного программирования |
Двойственность в задачах математического программирования
П.1. Экономическая интерпретация двойственных задач
Рассмотрим две фирмы. Первая фирма имеет налаженное производство определенного числа продукции, запасы сырья и получает прибыль от реализации готовых изделий. Вторая фирма имеет деньги и желание перекупить ресурсы у первой фирмы. Составим экономико-математические модели поведения двух указанных фирм.
Первая фирма. Пусть производится 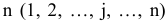 видов продукции, при этом используется m видов сырья, запасы которого
видов продукции, при этом используется m видов сырья, запасы которого 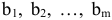 . При этом известна технология изготовления продукции, согласно которой на производство единицы продукции
. При этом известна технология изготовления продукции, согласно которой на производство единицы продукции 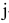 -ro вида идет
-ro вида идет 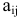 единиц ресурса
единиц ресурса 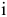 . Цена от реализации единицы продукции
. Цена от реализации единицы продукции 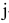 -го типа составляет
-го типа составляет 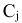 у.е. Требуется составить план выпуска продукции, который обеспечивал бы первой фирме максимальную прибыль.
у.е. Требуется составить план выпуска продукции, который обеспечивал бы первой фирме максимальную прибыль.
Перед нами типичная задача на использование ресурсов. Математическая модель данной задачи имеет вид:
Требуется максимизировать функцию
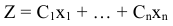
при ограничениях
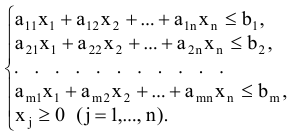
Здесь 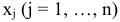 — количество единиц продукции
— количество единиц продукции 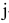 .
.
Вторая фирма. Перекупая сырье у первой фирмы, вторая фирма ставит перед собой задачу установить на сырье такие цены, чтобы общие затраты на закупку были минимальными.
Обозначим 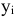 — цена в у.е. единицы сырья
— цена в у.е. единицы сырья 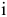 -го вида
-го вида 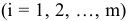 , получим, что общие затраты на приобретение сырья можно определить следующим образом:
, получим, что общие затраты на приобретение сырья можно определить следующим образом:
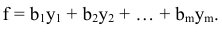
Функция 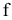 является целевой функцией задачи. Причем решение задачи будет состоять в поиске наименьшего значения
является целевой функцией задачи. Причем решение задачи будет состоять в поиске наименьшего значения 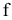 при заданных ограничениях.
при заданных ограничениях.
Систему ограничений задачи можно получить из следующих соображений. В каком случае первая фирма согласится продать свои ресурсы и прекратить выпуск п видов продукции? Только в том случае, когда прибыль от реализации единицы каждого вида продукции будет не больше, чем цена, установленная второй фирмой на ресурсы, затраченные на производство единицы этой продукции. Например, согласно технологии на единицу первого вида продукции затрачивается количество единиц первого ресурса 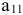 , второго —
, второго — 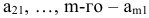 . Прибыль от реализации составляет
. Прибыль от реализации составляет 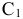 у.е. Таким образом, для совершения сделки необходимо выполнение неравенства
у.е. Таким образом, для совершения сделки необходимо выполнение неравенства
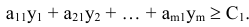
Рассуждая аналогичным образом, получим систему неравенств
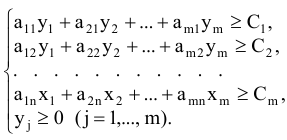
Сформулированные выше задачи называются симметричными двойственными задачами или просто двойственными задачами. Очевидно, что вторую задачу можно было построить по первой, не вдаваясь в экономический смысл. Для этого достаточно запомнить несколько правил.
- Если одна задача состоит в отыскании минимума целевой функции, то целью другой задачи будет нахождение максимума функции.
- Число условий ограничений одной задачи равно числу неизвестных переменных другой задачи.
- Коэффициенты в целевой функции одной задачи являются свободными членами в системе ограничений другой.
- Матрицы при переменных в системах ограничений задач являются транспонированными друг другу (см. [8]).
- При стандартной записи двойственных задач в системе ограничений задачи на максимум все знаки неравенств
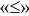 (использовать запасов не более, чем …), для задачи на минимум
(использовать запасов не более, чем …), для задачи на минимум 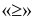 (затратить средств не менее, чем…).
(затратить средств не менее, чем…). - В одной и другой задаче имеются условия неотрицательности.
Обычно задачу, которую ставят первой, называют исходной задачей, задачу, которая составляется по исходной задаче, — двойственной задачей (см. табл. 5.1).

Замечание 5.1. Систему 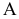 ограничений
ограничений 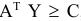 , используя правило умножения матриц, можно переписать следующим образом:
, используя правило умножения матриц, можно переписать следующим образом:
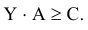
П.2. Теоремы двойственности
Как видно из предыдущего пункта, формулировка двойственной задачи целиком определяется формулировкой исходной задачи. Логичным было бы предположить, что и решение двойственной задачи определяется решением исходной задачи. Такое соответствие между решениями исходной и двойственной задач устанавливают теоремы двойственности.
Теорема 5.1. (первая теорема двойственности) Если из пары двойственных задач одна имеет оптимальное решение, то и другая задача имеет оптимальное решение, причем
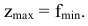
Если целевая функция одной из задач неограниченна, то другая задача не имеет решения.
Перед доказательством теоремы договоримся о некоторых дополнительных условиях, не влияющих на общность утверждения, и обозначениях.
Положим, что найдено решение задачи линейного программирования, в которой максимизируется функция
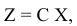
где
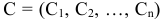
матрица строка,
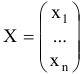
рая удовлетворяет ограничениям
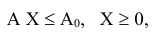
где
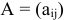
матрица коэффициентов при переменных,
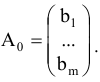
Для решения поставленной задачи симплексным методом необходимо было все неравенства привести к уравнениям путем прибавления дополнительных неотрицательных переменных
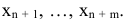
При этом ограничения запишутся в виде
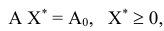
где
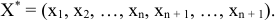
Положим, что поставленная задача обладает оптимальным планом 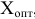 , причем базисными переменными являются
, причем базисными переменными являются 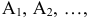 . Векторы
. Векторы 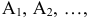
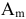 образуют базис, координаты векторов составляют единичную матрицу
образуют базис, координаты векторов составляют единичную матрицу 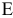 размером
размером 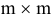 .
.
Двойственной для задач (5.1) и (5.2) является следующая задача
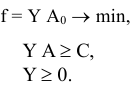
Доказательство.
Выбираем из матрицы 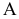 те столбцы, которые соответствуют базисным векторам в оптимальном решении задачи. Обозначим полученную матрицу через
те столбцы, которые соответствуют базисным векторам в оптимальном решении задачи. Обозначим полученную матрицу через
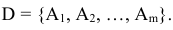
Для каждого вектора 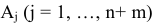 существует вектор
существует вектор 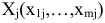 такой,что
такой,что
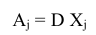
или
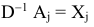
где 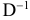 обозначает матрицу, обратную
обозначает матрицу, обратную 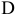 .
.
Для оптимального плана
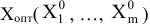
справедливы соотношения:
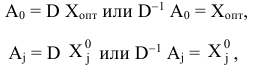
где
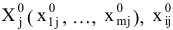
координаты вектора 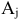 в оазисе
в оазисе  .
.
Поскольку по предположению план 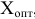 является оптимальным, то согласно теореме 4.1 выполняются соотношения
является оптимальным, то согласно теореме 4.1 выполняются соотношения
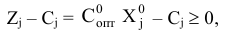
где
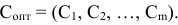
Будем искать оптимальный план двойственной задачи (5.4), (5.5) в виде
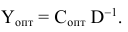
Для того, чтобы доказать, что план
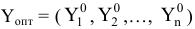
является оптимальным, необходимо показать, что выполняются два условия:
1) для вектора 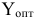 справедливы неравенства (5.5), т.е.
справедливы неравенства (5.5), т.е. 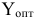 является решением двойственной задачи;
является решением двойственной задачи;
2) для других решений 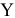 двойственной задачи выполняются условия
двойственной задачи выполняются условия 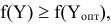 т.е.
т.е. 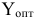 является оптимальным планом двойственной задачи.
является оптимальным планом двойственной задачи.
Докажем, что первое условие выполняется для каждого вектора 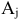
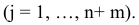
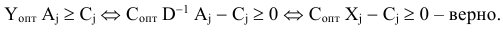
Значит, первое условие выполняется.
Докажем, что план 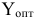 является оптимальным. Перепишем целевую функцию (5.4) следующим образом
является оптимальным. Перепишем целевую функцию (5.4) следующим образом
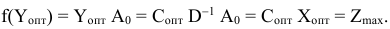
Рассмотрим любой другой план двойственной задачи 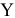 . Для него выполняются неравенства
. Для него выполняются неравенства
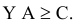
Умножим неравенства (5.9) с правой стороны на неотрицательную матрицу 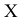 , являющуюся произвольным планом исходной задачи. Получим
, являющуюся произвольным планом исходной задачи. Получим
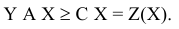
С другой стороны, для плана 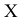 выполняются соотношения
выполняются соотношения
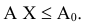
Умножим обе части (5.10) слева на матрицу 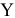 , получим
, получим
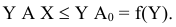
Таким образом
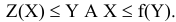
Полученное соотношение справедливо для любых планов исходной и двойственной задач, в том числе и для оптимальных, т.е.
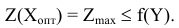
Это означает, что для любого плана двойственной задачи выполняется условие 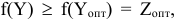 т.е.
т.е. 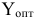 является оптимальным планом двойственной задачи.
является оптимальным планом двойственной задачи.
Докажем вторую часть утверждения теоремы. Пусть линейная функция исходной задачи не ограничена сверху. Тогда из (5.11) следует, что 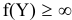 . Это выражение лишено смысла, следовательно, двойственная задача не имеет решений.
. Это выражение лишено смысла, следовательно, двойственная задача не имеет решений.
Первая теорема двойственности имеет совершенно ясный экономический смысл. Так цены 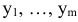 получили название учетных или теневых цен. В отличии от цен на продукцию
получили название учетных или теневых цен. В отличии от цен на продукцию  которые задаются до начала производства извне, теневые цены на ресурсы определяются только в процессе решения задачи. Согласно первой теории двойственности план производства
которые задаются до начала производства извне, теневые цены на ресурсы определяются только в процессе решения задачи. Согласно первой теории двойственности план производства 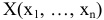 и учетный набор цен на ресурсы
и учетный набор цен на ресурсы 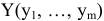 оказываются оптимальными в том и только том случае, когда прибыль от реализации продукции, найденная при известных ценах
оказываются оптимальными в том и только том случае, когда прибыль от реализации продукции, найденная при известных ценах  равна затратам на ресурсы по учетным ценам
равна затратам на ресурсы по учетным ценам 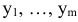 .
.
Очевидно, что при увеличении прибыльности первого предприятия, описанного в п.1 данного параграфа, второму предприятию будет сложнее (в смысле денежных затрат) перекупить у него ресурсы. Данный факт нашел свое отражение в знаменитом фильме с участием Дж.Фокса «Секрет его успеха». Опуская комедийные повороты сюжета и блестящую игру актеров, можно сказать, что в фильме сталкиваются две экономические концепции. Старое управление крупной компании, столкнувшись с угрозой быть купленной конкурентами, ведет политику на жесткую экономию и сокращение производства. Молодой менеджер, только что окончивший университет, напротив предлагает шаги для быстрого экономического развития, полагая, что ни у кого не хватит средств купить прибыльную, перспективную компанию. В результате он оказывается прав. Следует традиционный happy end, участие в котором, несомненно, принимали труды Канторовича и Данцига.
Перед доказательством теоремы 5.1 в условие исходной задачи были введены дополнительные переменные  . Вторая теорема двойственности устанавливает связь между первоначальными переменными двойственной задачи
. Вторая теорема двойственности устанавливает связь между первоначальными переменными двойственной задачи 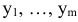 и дополнительными переменными исходной задачи.
и дополнительными переменными исходной задачи.
Теорема 5.2. (Вторая теорема двойственности4) Положительным компонентам оптимального решения одной из взаимно двойственных симметричных задач соответствуют нулевые компоненты оптимального решения другой задачи, т.е. для любых
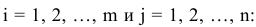
если
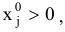
то
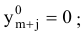
если
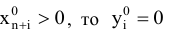
и наоборот,
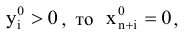
если
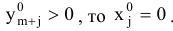
Доказательство. С учетом введения дополнительных переменных системы ограничений исходной и двойственной задач будет выглядеть следующим образом:
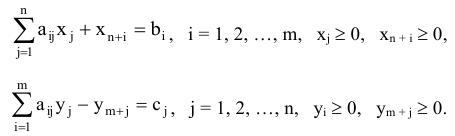
Выразим из (5.12) и (5.13) дополнительные переменные.
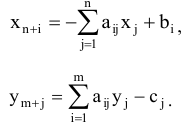
Умножим все уравнения (5.14) на соответствующие переменные 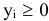 , а все уравнения (5.15) на
, а все уравнения (5.15) на 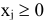 . Получим
. Получим
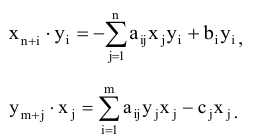
Сложим все равенства (5.16) и все равенства (5.17), получим:
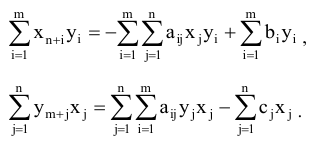
Положим, что планы
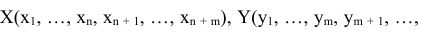
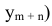
оптимальные, тогда
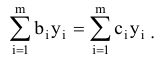
Складывая (5.18) и (5.19), получим
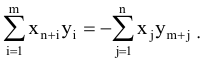
Поскольку
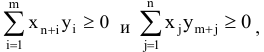
то полученное соотношение может выполняться только при условии, что
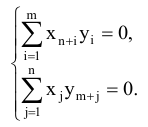
Условия (5.20) будут выполняться, если каждое из слагаемых в уравнениях будет равно нулю, т.е.
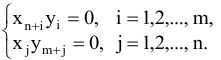
Таким образом, утверждение теоремы доказано.
Используя утверждения теорем 5.1, 5.2, рассмотрим, как, имея решение только одной из двойственных задач, можно построить решение другой.
Во-первых, оптимальные значения целевых функций двойственных задач совпадают.
Согласно результатам теоремы 5.1 оптимальный план двойственной задачи можно получить по формуле
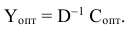
Однако, если использовать симплексную таблицу, то можно обнаружить, что в ней содержится не только решение исходной задачи, но и матрица 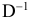 а также значение
а также значение 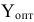 .
.
Действительно, при решении задачи на максимум общий вид симплексной таблицы перед первой итерацией следующий.

Последние m векторов  образуют единичную матрицу
образуют единичную матрицу 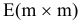 .
.
Положим, что при оптимальном плане в базис входят векторы  . Тогда симплексная таблица при последней итерации будет иметь вид.
. Тогда симплексная таблица при последней итерации будет иметь вид.
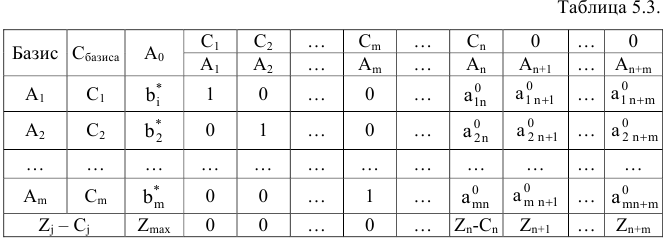
При этом последние  столбцов образуют матрицу
столбцов образуют матрицу 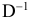 которая получена методом присоединения единичной матрицы (см. [8]). Оценки
которая получена методом присоединения единичной матрицы (см. [8]). Оценки 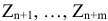 рассчитываются по формуле
рассчитываются по формуле
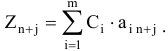
Таким образом, согласно теореме 5.2, устанавливающей соответствие между переменными 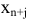 и
и 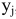 получим
получим
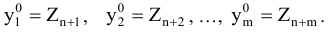
Если же исходная задача заключается в нахождении минимума функции, то добавочные переменные 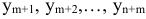 входят со знаком «минус», обратную матрицу —
входят со знаком «минус», обратную матрицу — 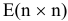 . В этом случае будут справедливы соотношения:
. В этом случае будут справедливы соотношения:
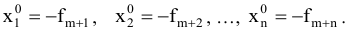
| Графический метод решения задач линейного программирования |
Задача №5.1.
Предприятие выпускает два вида продукции. Для производства единицы продукции первого типа требуется 12 кг ресурсов 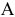 , 4 кг ресурсов
, 4 кг ресурсов 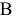 и 2 кг ресурсов
и 2 кг ресурсов 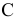 . Для производства единицы продукции второго вида затраты ресурсов следующие:
. Для производства единицы продукции второго вида затраты ресурсов следующие: 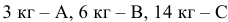 . Запасы ресурсов
. Запасы ресурсов 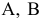 и
и 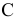 составляют 264 кг, 148 кг, 280 кг соответственно. Прибыль от реализации единицы первой продукции — 6 у.е., второй — 4 у.е. Требуется поставить для данной задачи двойственную и найти оптимальные значения и оптимальные планы задач.
составляют 264 кг, 148 кг, 280 кг соответственно. Прибыль от реализации единицы первой продукции — 6 у.е., второй — 4 у.е. Требуется поставить для данной задачи двойственную и найти оптимальные значения и оптимальные планы задач.
Решение:
Экономико-математическая модель исходной задачи имеет вид:
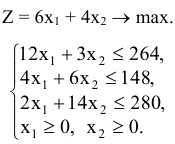
Здесь 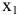 — количество единиц продукции первого вида,
— количество единиц продукции первого вида, 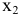 — количество единиц продукции второго вида.
— количество единиц продукции второго вида.
Модель двойственной задачи имеет вид:
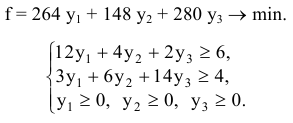
Здесь 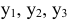 — теневые цены на ресурсы
— теневые цены на ресурсы 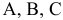 соответственно.
соответственно.
Решим исходную задачу симплексным методом. Для этого введем дополнительные переменные 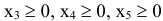 .
.
Составим симплексную таблицу.
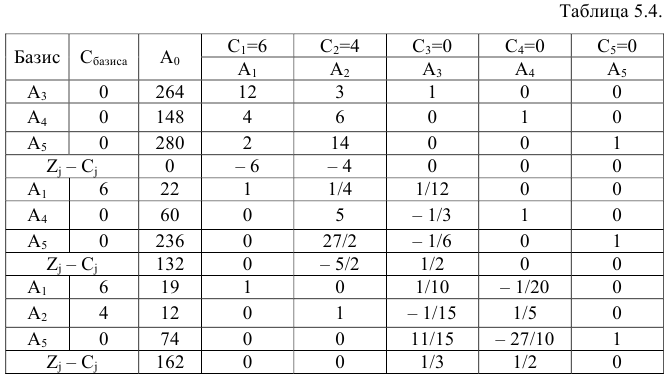
Поскольку в строке 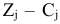 после второй итерации нет отрицательных чисел, то полученный план является оптимальным.
после второй итерации нет отрицательных чисел, то полученный план является оптимальным.
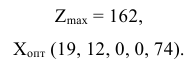
Запишем решение двойственной задачи. Согласно теореме 5.1
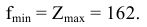
Оптимальный план двойственной задачи найдем по итоговым оценкам 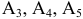 :
:
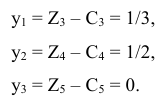
Сделаем проверку. Для этого подставим значения 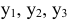 в целевую функцию
в целевую функцию
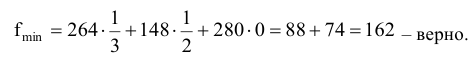
П.З. Объективно обусловленные оценки
Л.В. Канторович назвал компонент ы оптимального плана двойственной задачи объективно обусловленными оценками. Поясним экономический смысл этих оценок, используя результаты примера 5.1.
Значения добавленных переменных
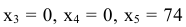
равны остаткам ресурсов 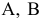 и
и 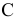 соответственно. Очевидно, что ресурсы
соответственно. Очевидно, что ресурсы 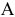 и
и 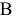 израсходованы полностью. Остаток ресурса
израсходованы полностью. Остаток ресурса 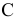 составляет 74 кг. В оптимальном решении двойственной задачи нулевым переменным
составляет 74 кг. В оптимальном решении двойственной задачи нулевым переменным 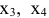 соответствуют ненулевые переменные
соответствуют ненулевые переменные
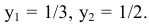
Ненулевой добавочной переменной 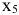 соответствует переменная
соответствует переменная 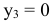 .
.
Таким образом, объективно обусловленные оценки ресурсов определяют степень дефицитности ресурсов: по оптимальному плану производства дефицитные ресурсы получают ненулевые оценки, а недефицитные — нулевые оценки.
П.4. Несимметричные двойственные задачи
Помимо симметричных двойственных задач в исследовании операций рассматриваются и несимметричные двойственные задачи. В таких задачах система ограничений исходной задачи задается в виде уравнений, а двойственной — в виде неравенств, причем в последней переменные могут быть и отрицательными.
В матричной форме несимметричные двойственные задачи записываются следующим образом.

Для несимметричных двойственных задач справедлива основная теорема двойственности — теорема 5.1.
| Заказать работу по линейному программированию |
Транспортная задача
ПЛ. Постановка транспортной задачи линейного программирования
Особое место в линейном программировании занимает так называемая транспортная задача. Традиционно она формулируется следующим образом.
Некоторый однородный продукт сосредоточен у 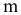 поставщиков
поставщиков 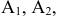
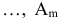 в количестве
в количестве 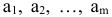 единиц соответственно. В данном товаре нуждаются
единиц соответственно. В данном товаре нуждаются 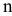 потребителей
потребителей 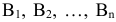 причем их запросы составляют
причем их запросы составляют 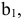
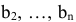 единиц товара соответственно. Стоимость перевозки единицы товара
единиц товара соответственно. Стоимость перевозки единицы товара 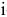 -го поставщика
-го поставщика 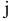 -му потребителю составляет
-му потребителю составляет 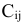 у.е.
у.е.
Необходимо составить план перевозок, позволяющий вывести все грузы, удовлетворить все потребности и имеющий минимальную стоимость.
К настоящему времени транспортная задача нашла свое применение в областях от теоретической физики до планирования экономических процессов.
Для удобства условия транспортной задачи задают в виде таблицы.

В случае. Если суммарные запасы совпадают с суммарными потребностями, транспортную задачу называют закрытой.
В противоположном случае, то есть, если запасы недостаточны или наоборот превышают потребности, то транспортная задача называется открытой.
Составим экономико-математическую модель закрытой транспортной задачи.
Пусть 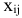 — количество продукта, перевозимого от
— количество продукта, перевозимого от 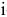 -го поставщика
-го поставщика 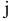 -му потребителю. Целевая функция задачи будет иметь вид:
-му потребителю. Целевая функция задачи будет иметь вид:
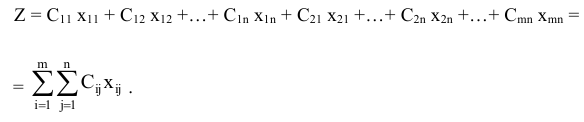
Систему ограничений получим из условий, что весь товар должен быть вывезен от поставщиков, и все потребители должны получить товар согласно своим запросам. Математически эти требования запишутся следующим образом:
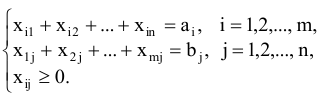
Как видно из экономико-математической модели, транспортная задача является частным случаем задачи ЛП.
Открытую транспортную задачу саму по себе рассматривают достаточно редко. Чаще ее сводят к закрытой транспортной задаче, пользуясь следующими правилами.
- Если суммарные запасы превышают суммарные потребности, т.е.
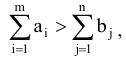
то следует ввести фиктивного потребителя. Его потребности будут равны разности
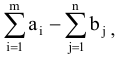
а цена перевозки ему товара от любого поставщика будет равна нулю.
- Если суммарные запасы меньше суммарных потребностей
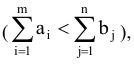
то следует ввести фиктивного поставщика, выделив ему запасы продукта в размере
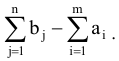
Цена перевозки также будет равна нулю.
Таким образом, любую открытую транспортную задачу можно свести к закрытой.
| Помощь по линейному программированию |
Задача №6.1.
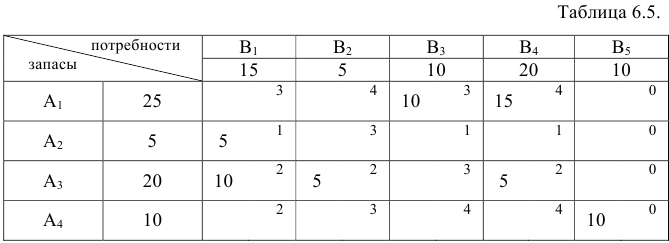
Перевести открытую транспортную задачу (см. таблицу 6.2) в закрытую.
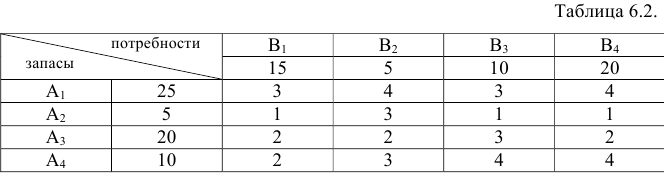
Решение:
Найдем суммарные запасы.
25 + 5 + 20 + 10 = 60. Найдем суммарные потребности
15 + 5 + 10 + 20 = 50. Таким образом, перед нами открытая задача, в которой запасы больше потребностей. Вводим фиктивного потребителя, выделяем ему 10 единиц продукта. При этом таблица 6.2 преобразуется следующим образом.
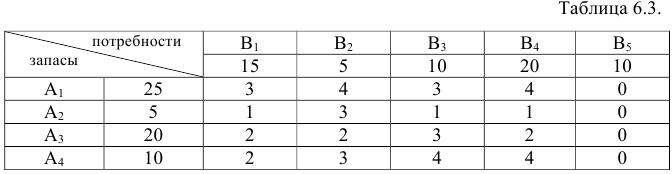
В данной задаче выполняются условия
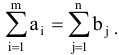
Значит открытая транспортная задача сведена к закрытой.
Как уже говорилось, транспортная задача является частным случаем задачи ЛП. Следовательно, ее можно решать, используя симплексный метод. Однако существуют менее громоздкие методы решения транспортной задачи. Один из них — метод потенциалов, будет рассмотрен в данном параграфе.
Как и для любой задачи ЛП при решении транспортной задачи возникают следующие вопросы:
1) Как составить первоначальный опорный план?
2) Как проверить план на оптимальность?
3) Как в случае, если план не оптимальный, перейти к лучшему (не худшему) плану?
П. 2. Построение первоначального опорного плана
Для транспортной задачи ЛП справедливы следующие утверждения.
Теорема 6.1. Любая закрытая транспортная задача имеет решение.
Теорема 6.2. Из 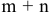 уравнений в системе ограничений транспортной задачи независимыми являются
уравнений в системе ограничений транспортной задачи независимыми являются 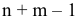 уравнений.
уравнений.
Приведенные утверждения примем без доказательств.
Согласно утверждению теорем 6.1 и 6.2 первоначальный опорный план транспортной задачи можно составить всегда, причем в матрице 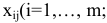
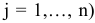 значений компонент опорного плана содержится
значений компонент опорного плана содержится 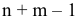 положительный компонент. Остальные компоненты равны нулю. Значения
положительный компонент. Остальные компоненты равны нулю. Значения 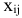 удобно проставлять прямо в таблице 6.1.
удобно проставлять прямо в таблице 6.1.
Существует несколько способов составления первоначального опорного плана.
- Метод северо-западного угла. Этот метод состоит в том, что заполнение таблицы 6.1 начинается последовательно с левой верхней ячейки, без учета стоимости перевозок.
- Метод наименьшей стоимости. В этом методе из всей таблицы выбирают клетку с наименьшей стоимостью
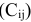 помещают туда наименьшее из чисел
помещают туда наименьшее из чисел 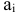 или
или 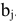 . Если потребности потребителя
. Если потребности потребителя 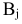 удовлетворены, то его исключают из рассмотрения. Обратно, если при заполнении клетки
удовлетворены, то его исключают из рассмотрения. Обратно, если при заполнении клетки 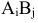 израсходованы все запасы, то в дальнейшем распределении поставок не участвует поставщик
израсходованы все запасы, то в дальнейшем распределении поставок не участвует поставщик 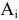 . После этого выбирают следующую клетку с наименьшей стоимостью и т.д.
. После этого выбирают следующую клетку с наименьшей стоимостью и т.д. - Метод двойного предпочтения. Этот метод особенно удобен в случае, когда таблица 6.1 велика. Суть его заключается в следующем. В каждом столбце знаком
 (или любым другим, как кому захочется) отмечается клетка, имеющая наименьшую стоимость
(или любым другим, как кому захочется) отмечается клетка, имеющая наименьшую стоимость 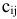 . Затем отмечается клетка, имеющая наименьшую стоимость в строке. В результате появятся клетки, имеющие отметки
. Затем отмечается клетка, имеющая наименьшую стоимость в строке. В результате появятся клетки, имеющие отметки 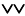 , клетки, имеющие отметку
, клетки, имеющие отметку  , и клетки, не имеющие отметок. В клетки
, и клетки, не имеющие отметок. В клетки 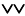 , помещают максимально возможные поставки, каждый раз, исключая соответствующих поставщиков или потребителей. Затем заполняются клетки
, помещают максимально возможные поставки, каждый раз, исключая соответствующих поставщиков или потребителей. Затем заполняются клетки  . Затем клетки без отметок с использованием метода наименьшей стоимости.
. Затем клетки без отметок с использованием метода наименьшей стоимости.
В среднем наилучший результат дает метод двойного предпочтения, а худший — метод северо-западного угла.
Замечание 6.1. Метод двойного предпочтения лучше именно в среднем. Какой метод окажется лучше в конкретной задаче сказать нельзя.
Задача №6.1 (продолжение).
Используя метод двойного предпочтения, составить первоначальный опорный план транспортной задачи.
Решение:
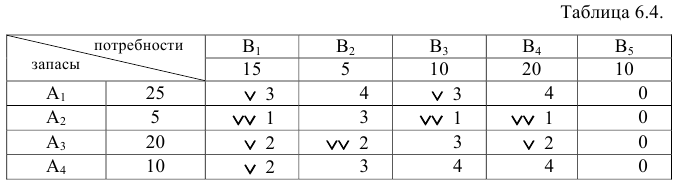
Замечание 6.2. Клетки в добавленном столбце Bs заполняются в последнюю очередь, несмотря на то, что имеют нулевую стоимость.
Две отметки получили клетки 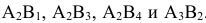 . Начнем составление опорного плана с заполнения клетки
. Начнем составление опорного плана с заполнения клетки 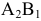 . Максимальная поставка в эту клетку составляет 5 ед. продукта
. Максимальная поставка в эту клетку составляет 5 ед. продукта 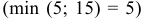 . При этом запасы поставщика
. При этом запасы поставщика 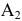 полностью исчерпаны, и ни одна из клеток строки
полностью исчерпаны, и ни одна из клеток строки 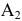 не может быть больше заполнена.
не может быть больше заполнена.
Следующую поставку делаем в клетку 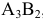 , поскольку это последняя клетка с двумя пометками, в которую можно сделать поставку. Максимальная поставка равна 5 ед. продукции. При этом потребности потребителя
, поскольку это последняя клетка с двумя пометками, в которую можно сделать поставку. Максимальная поставка равна 5 ед. продукции. При этом потребности потребителя 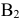 удовлетворены полностью, и клетки, расположенные в столбце
удовлетворены полностью, и клетки, расположенные в столбце 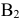 , не участвуют в дальнейшем рассмотрении.
, не участвуют в дальнейшем рассмотрении.
Заполняем теперь клетки, имеющие одну отметку, которые не находятся в строке 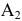 и столбце
и столбце 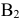 . Это клетки
. Это клетки
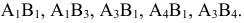
Сделаем максимальную поставку в клетку 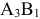 . Она равна 10 ед. продукта, т.к. 5 ед. продукта из необходимых 15 ед. были получены потребителем
. Она равна 10 ед. продукта, т.к. 5 ед. продукта из необходимых 15 ед. были получены потребителем 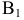 от поставщика
от поставщика 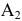 . Теперь потребности потребителя
. Теперь потребности потребителя 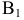 полностью удовлетворены, столбец
полностью удовлетворены, столбец 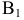 не рассматривается. Делаем поставку в клетку
не рассматривается. Делаем поставку в клетку 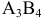 . Максимально возможная поставка равна 5 ед. продукта, оставшимся у поставщика
. Максимально возможная поставка равна 5 ед. продукта, оставшимся у поставщика 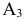 . При этом строка
. При этом строка 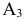 в дальнейшем распределении товара не участвует.
в дальнейшем распределении товара не участвует.
Больше клеток с отметками нет, поэтому оставшиеся клетки заполняются по методу наименьшей стоимости. Наименьшую стоимость имеет клетка 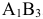 . Туда можно сделать максимальную поставку 10 ед. продукта. Потребности потребителя
. Туда можно сделать максимальную поставку 10 ед. продукта. Потребности потребителя 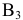 удовлетворены полностью. Столбец
удовлетворены полностью. Столбец 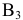 исключается из рассмотрения.
исключается из рассмотрения.
Остаются незаполненными клетки 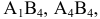 а также клетки добавочного столбца
а также клетки добавочного столбца 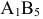 и
и 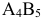 . Стоимость перевозки в клетках
. Стоимость перевозки в клетках 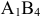 и
и 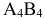 одинакова — 4 у.е. На выбор сделаем поставку 15 ед. продукции в клетку
одинакова — 4 у.е. На выбор сделаем поставку 15 ед. продукции в клетку 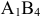 . Оставшиеся 10 ед. продукции у поставщика
. Оставшиеся 10 ед. продукции у поставщика 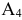 заносим в столбец фиктивного потребителя
заносим в столбец фиктивного потребителя 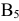 в клетку
в клетку 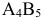 .
.
Первоначальное распределение товара закончено. Общая стоимость перевозок равна
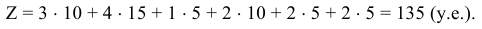
Замечание 6.2. При составлении первоначального плана перевозки удобно карандашом вычеркивать те строки и столбцы, которые выходят из рассмотрения.
Замечание 6.3. Типичные ошибки при составлении опорного плана появляются из-за того, что решающий забывает, сколько тот или иной поставщик доставил продукта тому или иному потребителю. Для проверки достаточно просуммировать поставки по строкам и столбцам и сравнить их с соответствующими запасами и потребностями, например, для первой строки 10+15 = 25-верно.
Вернемся к решению задачи 6.1. В первоначальном плане перевозок содержится 7 положительных компонент. Согласно утверждению теоремы 6.2 опорный план транспортной задачи должен содержать 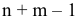 положительных компонент, т.е. 4 + 5 — 1 = 8. В полученном плане не хватает одной положительной компоненты. Такой план перевозок, в котором число положительных перевозок меньше, чем
положительных компонент, т.е. 4 + 5 — 1 = 8. В полученном плане не хватает одной положительной компоненты. Такой план перевозок, в котором число положительных перевозок меньше, чем 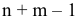 называется вырожденным опорным планом. Как будет видно в дальнейшем вырожденность не очень «испортит» процесс решения транспортной задачи.
называется вырожденным опорным планом. Как будет видно в дальнейшем вырожденность не очень «испортит» процесс решения транспортной задачи.
При составлении первоначального плана перевозок может возникнуть ситуация, когда число положительных компонент больше, чем 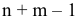 . В этом случае план не будет являться опорным, т.к. ему соответствует линейно зависимая система векторов. В этом случае можно уменьшить число занятых клеток до
. В этом случае план не будет являться опорным, т.к. ему соответствует линейно зависимая система векторов. В этом случае можно уменьшить число занятых клеток до 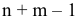 . Для этого следует рассмотреть одно из центральных понятий данной темы — понятие цикла.
. Для этого следует рассмотреть одно из центральных понятий данной темы — понятие цикла.
Определение 6.1. Циклом называется набор клеток вида 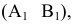
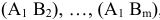 , в котором две и только две соседние клетки расположены в одном столбце или одной строке таблицы, причем последняя клетка находится в том же столбце, что и первая.
, в котором две и только две соседние клетки расположены в одном столбце или одной строке таблицы, причем последняя клетка находится в том же столбце, что и первая.
Построение цикла начинается с какой-либо занятой клетки. После этого двигаются по занятым клеткам, поворачивая в них под прямым углом, стараясь возвратиться к первоначальной клетке. Выражаясь шахматными терминами, движения в цикле могут осуществляться по правилам движения ладьи. Клетки, в которых происходит поворот цикла, называются вершина-
Опорный план и вырожденный опорный план обладают свойствами ацикличности, т.е. цикла, вершинами которого являются занятые клетки, не существует.
Если число занятых клеток больше, чем 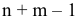 , то можно построить замкнутый цикл, с помощью которого число занятых клеток уменьшается. Построение цикла более подробно будет рассмотрено при дальнейшем решении примера 6.1.
, то можно построить замкнутый цикл, с помощью которого число занятых клеток уменьшается. Построение цикла более подробно будет рассмотрено при дальнейшем решении примера 6.1.
П. 3. Оценка плана транспортной задачи на оптимальность (метод потенциалов)
Метод потенциалов является одним из самых распространенных методов решения транспортной задачи линейного программирования.
Под потенциалами будем понимать набор чисел 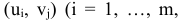
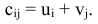 таких, что для занятых клеток выполняется условие
таких, что для занятых клеток выполняется условие
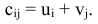
Если число занятых клеток 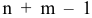 , то все значения потенциалов кроме одного определяются однозначно. Справедливо следующее утверждение.
, то все значения потенциалов кроме одного определяются однозначно. Справедливо следующее утверждение.
Теорема 6.3. Если план 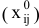 транспортной задачи является оптимальным, то для соответствующей ему системы потенциалов
транспортной задачи является оптимальным, то для соответствующей ему системы потенциалов 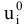 и
и 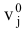 выполняются условия:
выполняются условия:
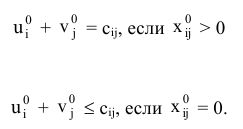
Таким образом, для проверки опорного плана на оптимальность можно воспользоваться следующим алгоритмом.
1) Задаем какой-либо потенциал. Удобно приравнять к нулю потенциал той строки или столбца, в которых больше всего занятых клеток.
2) Получим систему потенциалов из условия
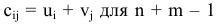
занятой клетки.
3) Составим оценочную матрицу 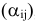 , элементы которой получаются следующим образом
, элементы которой получаются следующим образом 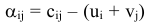 . Если среди элементов оценочной матрицы нет отрицательных, то план
. Если среди элементов оценочной матрицы нет отрицательных, то план 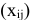 является оптимальным, в противоположном случае план не является оптимальным.
является оптимальным, в противоположном случае план не является оптимальным.
Задача №6.1 (продолжение).
Используя метод потенциалов, проверить на оптимальность первоначальный план перевозок.
Решение:
Перепишем таблицу 6.5 в следующем виде.
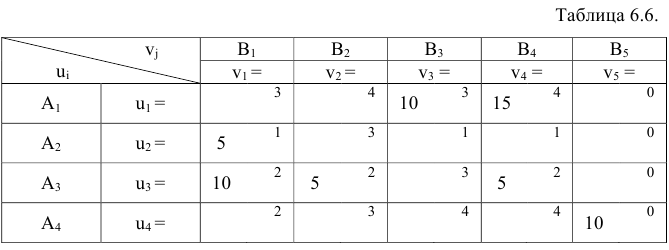
Наиболее удобно потенциалу 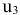 дать значение 0. Значение потенциалов
дать значение 0. Значение потенциалов 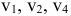 определим из системы.
определим из системы.
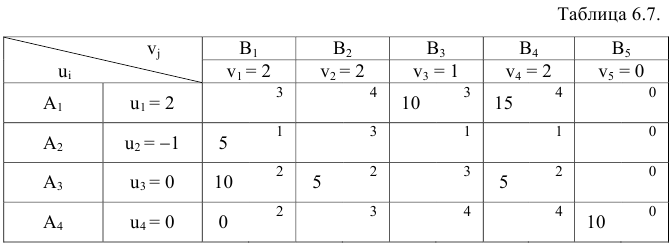
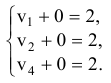
Зная потенциалы 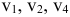 определим потенциалы
определим потенциалы 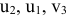 .
.
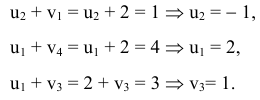
Больше ни одного потенциала определить нельзя. Это связано с тем, что полученный ранее опорный план является вырожденным. Не хватает одной заполненной клетки. Чтобы превратить вырожденный опорный план в невырожденный применяется следующий прием. Вводится фиктивная поставка размером 0 ед. продукта в незанятую клетку, соответствующую столбцу или строке, в которой находится только один неизвестный потенциал. Желательно, чтобы эта клетка не была среди добавленных и имела наименьшую стоимость.
Замечание 6.3. Случается, что приходится вводить не одну, а несколько фиктивных поставок. При этом, если ввести фиктивную поставку в клетку, которая находится на пересечении неизвестных потенциалов, то, естественно, ничего определить не получится. С этим связано замечание, что фиктивная поставка вводится в ту клетку, где неизвестен только один потенциал.
Делаем нулевую фиктивную поставку в клетку 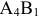 со стоимостью перевозки 2 у.е. Определяем оставшиеся потенциалы:
со стоимостью перевозки 2 у.е. Определяем оставшиеся потенциалы:
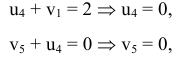
Система потенциалов построена.
Составим оценочную матрицу 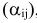 , рассчитывая ее элементы по формулам:
, рассчитывая ее элементы по формулам:
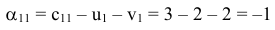
и т.д.,
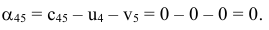
Получим

Индекс «0» означает номер итерации.
Поскольку среди элементов матрицы 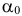 есть отрицательные (
есть отрицательные (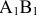 и
и 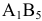 ), полученный первоначальный план перевозок не является оптимальным.
), полученный первоначальный план перевозок не является оптимальным.
П. 4. Переход от одного опорного плана транспортной задачи к другому
Переход от одного опорного плана к другому происходит по аналогичной с симплексным методом схеме. Для улучшения плана в клетку плана перевозок, которой соответствует отрицательный элемент в матрице оценок. При этом план улучшается (стоимость изменяется) на 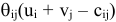 , где
, где 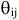 -размер поставки.
-размер поставки.
Для перераспределения груза нужно построить цикл с началом и концом в клетке, куда делается поставка. Такой цикл можно составить единственным образом, поскольку клеток с поставками будет 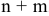 . В клетке, куда делается поставка, ставится знак «+». Далее поочередно подставляем знаки «-» и «+» в вершинах цикла. Затем находим наименьшее значение перевозки
. В клетке, куда делается поставка, ставится знак «+». Далее поочередно подставляем знаки «-» и «+» в вершинах цикла. Затем находим наименьшее значение перевозки 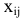 , стоящей в клетке со знаком «-». Это наибольшая возможная поставка в незанятую клетку
, стоящей в клетке со знаком «-». Это наибольшая возможная поставка в незанятую клетку 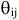 .
.
При перераспределении в клетках со знаком «-» вычитаем значение By из величины перевозки, в клетках со знаком «+» прибавляем.
В случае, если циклов несколько, выбирается тот, которому соответствует наибольшее значение 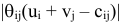 .
.
Задача №6.1 (продолжение).
Найти оптимальный план перевозок для транспортной задачи, заданной таблицей 6.2.
Решение:
В матрице (6.3) имеются два отрицательных элемента 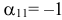 и
и 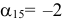 . Следовательно, можно сделать поставки в эти клетки. Составить циклы можно непосредственно в таблице 6.7, однако это требует известной доли аккуратности, которой обладают не все читатели. Удобнее составить упрощенную матрицу перевозок
. Следовательно, можно сделать поставки в эти клетки. Составить циклы можно непосредственно в таблице 6.7, однако это требует известной доли аккуратности, которой обладают не все читатели. Удобнее составить упрощенную матрицу перевозок
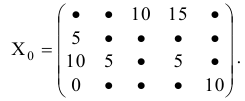
В матрице (6.4) знаком «•» обозначается незанятая клетка. Рассмотрим два цикла, с помощью которых делаются поставки в клетки 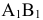 и
и 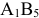 .
.
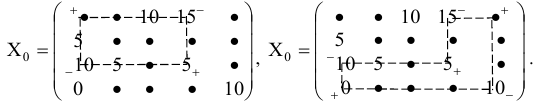
Определим экономию от поставки в клетку 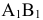 . В полученном цикле две вершины с отрицательными отметками
. В полученном цикле две вершины с отрицательными отметками 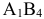 и
и 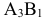 . Получим
. Получим
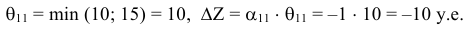
Проделаем аналогичную операцию в случае, когда поставка делается в клетку 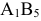 . Получается, что поставку в клетку
. Получается, что поставку в клетку 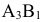 наиболее выгодна.
наиболее выгодна.
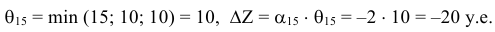
Делаем поставку в клетку 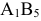 . Для этого в вершинах цикла, отмеченных знаком «+», добавим к поставкам 10 ед. продукта, в вершинах, отмеченных знаком «-» отнимем 10 ед. продукта. Получим
. Для этого в вершинах цикла, отмеченных знаком «+», добавим к поставкам 10 ед. продукта, в вершинах, отмеченных знаком «-» отнимем 10 ед. продукта. Получим
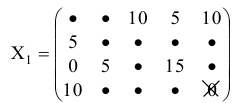
В плане 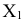 имеется 9 занятых клеток, тогда как опорный невырожденный план должен содержать
имеется 9 занятых клеток, тогда как опорный невырожденный план должен содержать 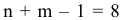 занятых клеток. Для того, чтобы план
занятых клеток. Для того, чтобы план 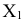 стал опорным, нужно вычеркнуть одну из фиктивных нулевых перевозок. Вычеркиваем ноль в столбце фиктивного потребителя
стал опорным, нужно вычеркнуть одну из фиктивных нулевых перевозок. Вычеркиваем ноль в столбце фиктивного потребителя 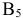 .
.
Новый план 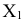 нужно оценить на оптимальность. Можно снова построить систему потенциалов, однако для ручных расчетов удобнее воспользоваться следующим приемом.
нужно оценить на оптимальность. Можно снова построить систему потенциалов, однако для ручных расчетов удобнее воспользоваться следующим приемом.
Подчеркнем в матрице 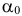 те элементы, которые соответствуют занятым клеткам матрицы
те элементы, которые соответствуют занятым клеткам матрицы 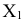 .
.

Поскольку клетка 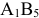 теперь занята, то в новой матрице оценок
теперь занята, то в новой матрице оценок 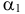 i элемент
i элемент 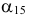 должен быть равен нулю. Для этого достаточно уменьшить на 2 либо потенциал
должен быть равен нулю. Для этого достаточно уменьшить на 2 либо потенциал 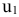 , либо потенциал
, либо потенциал 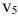 . При этом либо к строке
. При этом либо к строке 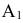 , либо к строке
, либо к строке  нужно прибавить 2. В том и в другом случае итоговые результаты совпадут. Однако для упрощения расчетов лучше выбрать ту строку или столбец, где меньше подчеркнутых элементов. В этом смысле гораздо «лучше» столбец
нужно прибавить 2. В том и в другом случае итоговые результаты совпадут. Однако для упрощения расчетов лучше выбрать ту строку или столбец, где меньше подчеркнутых элементов. В этом смысле гораздо «лучше» столбец  . Прибавляя к столбцу
. Прибавляя к столбцу  двойку, мы не затрагиваем ни одной подчеркнутой клетки, следовательно не надо менять ни один из оставшихся потенциалов. Получим
двойку, мы не затрагиваем ни одной подчеркнутой клетки, следовательно не надо менять ни один из оставшихся потенциалов. Получим
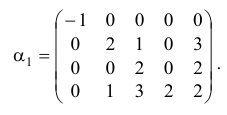
В матрице 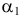 остался отрицательный элемент
остался отрицательный элемент 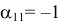 . Составляем цикл с началом в клетке
. Составляем цикл с началом в клетке 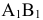 .
.
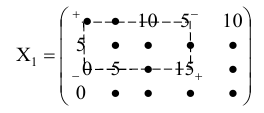
Поскольку 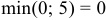 , то экономия от поставки равна нулю, т.е. план не ухудшится.
, то экономия от поставки равна нулю, т.е. план не ухудшится.
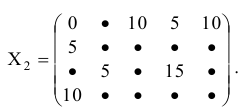
В матрице 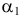 отметим те клетки, которые соответствуют занятым клеткам матрицы
отметим те клетки, которые соответствуют занятым клеткам матрицы 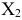 . Прибавим к столбцу
. Прибавим к столбцу 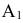 единицу, чтобы получить
единицу, чтобы получить 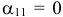 .
.
При этом изменяются подчеркнутые клетки 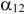 и
и 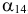 , которые должны быть равными нулю. Изменим потенциалы
, которые должны быть равными нулю. Изменим потенциалы 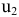 и
и 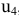 , отняв от строк
, отняв от строк 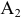 и
и 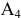 единицу. Теперь всем занятым клеткам в матрице
единицу. Теперь всем занятым клеткам в матрице 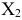 соответствуют нули в матрице
соответствуют нули в матрице 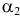 .
.
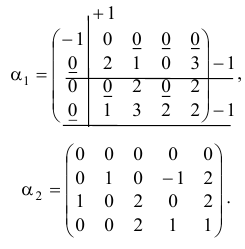
Делаем поставку в клетку 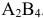 .
.
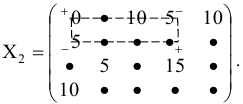
Найдем экономию от данной поставки
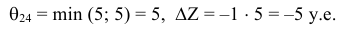
Получим (мнимый ноль в клетке 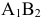 вычеркиваем)
вычеркиваем)
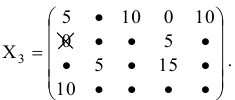
Проведем преобразование оценочной матрицы аналогично тому, как это делалось раньше.
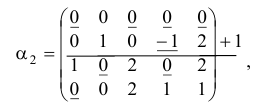
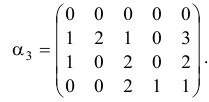
Поскольку в матрице 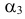 нет отрицательных элементов, то план
нет отрицательных элементов, то план 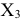 является оптимальным.
является оптимальным.
Найдем общую стоимость перевозок
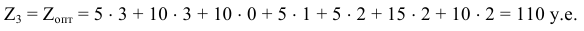
Данный результат можно было получить иным способом, взяв за основу затраты на перевозки в первоначальном опорном плане:
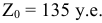
За три итерации была достигнута экономия
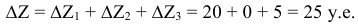
Тогда
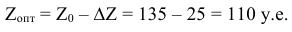
Такой двойной подсчет может служить простой проверкой правильности расчетов.
Проведем небольшой анализ решения.
Оптимальный план перевозок задается матрицей 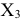 , причем общая стоимость перевозок
, причем общая стоимость перевозок 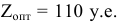 У первого поставщика осталось не вывезенными 10 ед. продукта (вспомним, что клетка
У первого поставщика осталось не вывезенными 10 ед. продукта (вспомним, что клетка 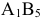 соответствует фиктивному потребителю). Можно выяснить, является ли полученный оптимальный план перевозок единственным. Для этого нужно в матрице
соответствует фиктивному потребителю). Можно выяснить, является ли полученный оптимальный план перевозок единственным. Для этого нужно в матрице 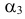 подчеркнуть элементы, соответствующие занятым клеткам в матрице
подчеркнуть элементы, соответствующие занятым клеткам в матрице 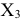 .
.

В матрице 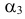 есть нулевые элементы, которые не соответствуют занятым клеткам матрицы
есть нулевые элементы, которые не соответствуют занятым клеткам матрицы 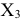 , поэтому полученное оптимальное решение не единственное (можно сделать поставку в клетки с нулевыми оценками, от этого стоимость перевозок не изменится). Более того, согласно свойствам решений задачи линейного программирования, линейная комбинация оптимальных решений транспортной задачи будет оптимальным решением.
, поэтому полученное оптимальное решение не единственное (можно сделать поставку в клетки с нулевыми оценками, от этого стоимость перевозок не изменится). Более того, согласно свойствам решений задачи линейного программирования, линейная комбинация оптимальных решений транспортной задачи будет оптимальным решением.
| Контрольная работа линейное программирование |
Элементы целочисленного математического программирования
ПЛ. Постановка задачи целочисленного математического программирования
В некоторых экономико-математических моделях к традиционным ограничениям добавляется требование целочисленного решения. Действительно, если речь идет о производстве различных типов тракторов, то ответ «нужно произвести 6,5 штук тракторов первого типа» вызовет недоумение. К типичным экономическим задачам, в которых решение должно даваться в целых числах, относятся задачи об оптимальном раскрое материала, об оптимальном использовании оборудования и т.д.
Общую постановку задачи целочисленного линейного программирования можно сформулировать следующим образом.
Найти минимальное (максимальное) значение линейной функции
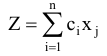
при ограничениях
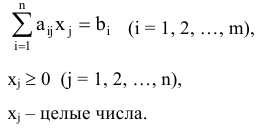
Можно заметить, что транспортная задача относится к задачам целочисленного программирования. При этом решение транспортной задачи в общем можно упростить по сравнению с решением обычной задачи линейного программирования. С другими задачами целочисленного программирования дело обстоит в точности наоборот. Традиционно задачи целочисленного программирования относятся к одним из наиболее сложных задач исследования операций.
П.2. Методы отсечения
Наиболее развитыми к настоящему времени численными методами решения задач целочисленного линейного программирования являются методы отсечения и комбинаторные методы.
В работе Э.А. Мухачевой и Г.Ш. Рубинштейна методы отсечения удачно сравниваются с работой скульптора, который для изготовления скульптуры берет каменную глыбу и отсекает от нее все ненужное. В качестве глыбы в задачах целочисленного программирования выступает многогранник решений (см. рис. 7.1).
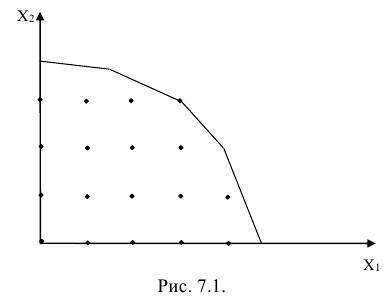
С помощью методов линейного программирования находится решение 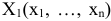 , при котором целевая функция достигает оптимального значения. Если вектор
, при котором целевая функция достигает оптимального значения. Если вектор 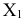 нецелочисленный, то вводится новое линейное ограничение, которое отсекает от многоугольника ограничений найденное решение, но оставляет все целочисленные решения. Вновь ищется оптимальное решение, если оно вновь оказывается целочисленным, то процесс продолжается далее.
нецелочисленный, то вводится новое линейное ограничение, которое отсекает от многоугольника ограничений найденное решение, но оставляет все целочисленные решения. Вновь ищется оптимальное решение, если оно вновь оказывается целочисленным, то процесс продолжается далее.
Остановимся подробнее на методе, предложенном американским математиком Гомори. Рассмотрим его на примере.
| Линейное программирование в Excel |
Задача №7.1.
Методом Гомори решить следующую задачу. Для приобретения оборудования по переработке молока фермер выделяет 18 ден. ед. Оборудование должно быть размещено на территории, не превышающей 6 соток. Можно заказать оборудование двух видов 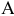 и
и 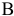 . Единица оборудования
. Единица оборудования 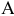 стоит 4 ден. ед. и занимает площадь в 1 сотку. Ее использование приносит доход в 3 ден. ед. Единица оборудования
стоит 4 ден. ед. и занимает площадь в 1 сотку. Ее использование приносит доход в 3 ден. ед. Единица оборудования 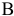 стоит 6 ден. ед., занимет площадь 2 сотки и приносит доход 2 ден. ед.
стоит 6 ден. ед., занимет площадь 2 сотки и приносит доход 2 ден. ед.
Фермер не может приобрести более 5 ед. оборудования  и более 4 ед. оборудования
и более 4 ед. оборудования  .
.
Решение:
Экономико-математическая модель сформулированной задачи имеет вид:
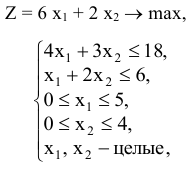
где 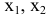 — число единиц оборудования
— число единиц оборудования  и
и  соответственно.
соответственно.
Решим задачу (7.1) (воспользуемся симплексным методом решения).
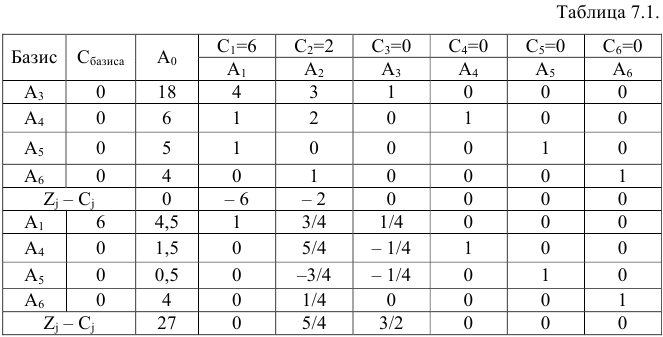
Обозначим 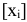 и
и 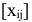 целые части чисел
целые части чисел 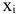 и
и 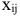 соответственно. Величины
соответственно. Величины
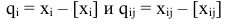
неотрицательны.
Можно показать, что справедливо неравенство

В случае, если решение задачи не целочисленное, неравенство (7.2) используется в качестве дополнительного ограничения. Для этого неравенство (7.2) необходимо добавить вспомогательную переменную 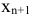
В нашем случае
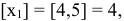
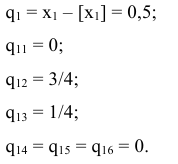
Значит,
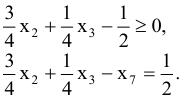
Замечание 7,1. Если в плане несколько дробных значений 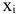 выбирают то, значение
выбирают то, значение 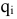 для которого максимальное.
для которого максимальное.
Условия новой задачи будут выглядеть следующим образом
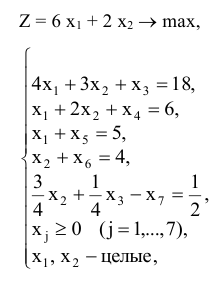
Решим задачу симплексным методом.
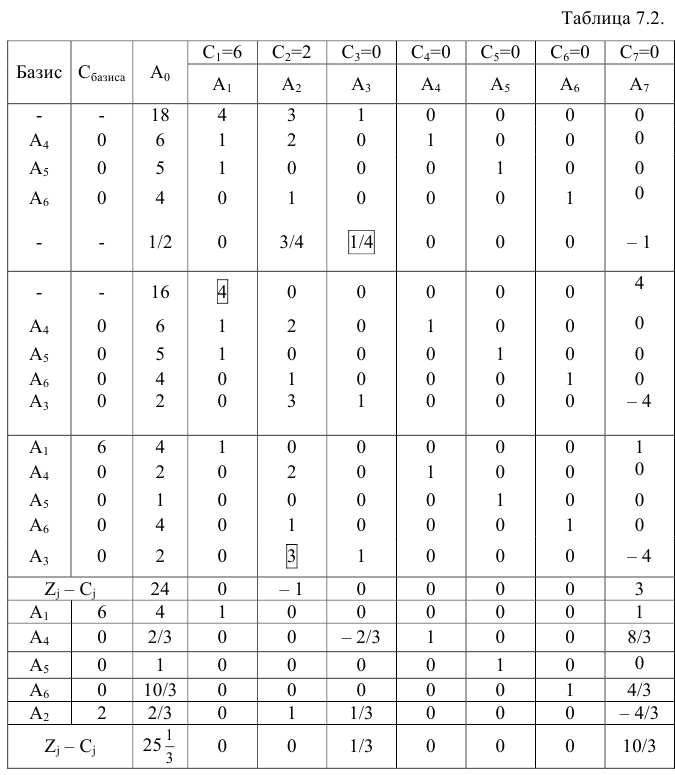
Полученное решение задачи (7.3)
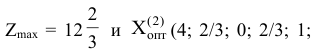
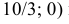
не подходит, поскольку 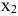 — дробное.
— дробное.
Вводим дополнительное ограничение, используя строку 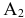 таблицы 7.2. Получим
таблицы 7.2. Получим
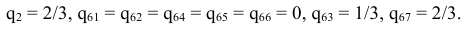
Новое ограничение имеет вид
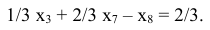
Сформулируем новую задачу
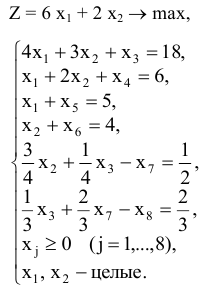
Решая задачу (7.4) симплексным методом получим
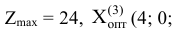
В плане 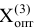 нет дробных компонент. Задача решена.
нет дробных компонент. Задача решена.
П.З. Комбинаторные методы
Комбинаторные методы в значительно большей мере, чем методы отсечения учитывают дискретный характер задач целочисленного программирования. К настоящему времени существует достаточно много комбинаторных методов. В работе рассмотрим наиболее известный из них — метод ветвей и границ. Данный метод заключается в том, что из исходной задачи составляют несколько задач, из них рассматриваются только перспективные. Неперспективные отбрасываются. Рассмотрим работу метода на предыдущем примере.
Задача №7.2.
Решить методом ветвей и границ задачу линейного программирования
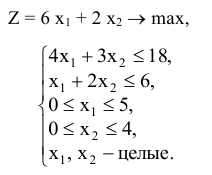
Решение:
Решая исходную задачу (7.5), получим
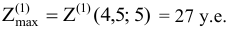
Данная задача не обладает целочисленным планом, поскольку 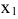 -дробное. Так как оптимальное целочисленное решение не должно содержать полосу 4 <
-дробное. Так как оптимальное целочисленное решение не должно содержать полосу 4 < 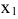 < 5, исключаем ее. Получим две новые задачи:
< 5, исключаем ее. Получим две новые задачи:
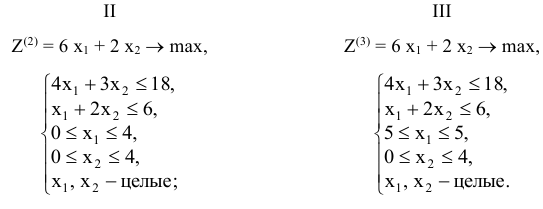
Условия задачи III противоречивы, поэтому исключим ее из дальнейшего рассмотрения.
Решая задачу II, получим
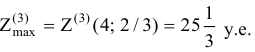
Разобьем задачу II на две задачи линейного программирования IV и V, исключив полосу 0 < 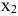 < 1.
< 1.
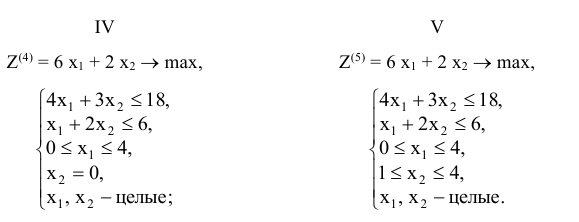
Решая задачу IV, получим
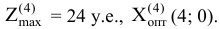
Полученное решение является целочисленным, поэтому движение по этой ветви прекращается.
Решаем задачу V. Получаем
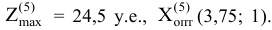
Решение нецелочисленное. Исключаем из рассмотрения полосу 3 < 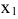 <4. Получаем две новые задачи:
<4. Получаем две новые задачи:
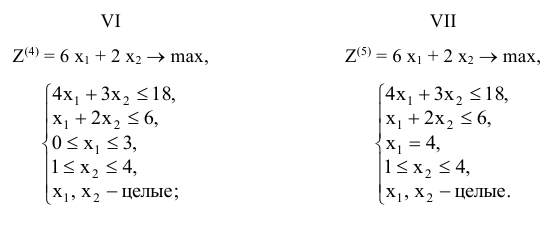
Условия задачи VII являются противоречивыми.
Решая задачу VI, получим
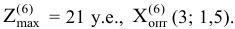
Несмотря на то, что решение задачи VI нецелочисленное, нет смысла продолжать ее решение, поскольку уже был получен результат
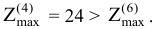
Решение закончено.
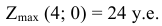
| Курсовая работа по линейному программированию |
Характеристика задач нечеткого математического программирования
В последние годы, наряду с «классическими» задачами математического программирования, появились задачи в так называемой «нечеткой» постановке.
Классическое математическое программирование и его разновидности — в значительной степени нормативная методология эффективного выбора. Нечеткое же программирование выделяет естественную множественность неточно определенных целей, значений и ограничений. При этом оптимальность определяется и в терминах поведения, и как качество, присущее решению (основные сведения об аппарате нечеткой логики приведены в Приложении А).
Главная цель нечеткого математического программирования (НМП) -помочь лицу, принимающему решение, разобраться в выдвинутых им допущениях. Нечеткий подход не подменяет собой простейшего анализа в поисках разумной точности. Он облегчает задачу лица, принимающего решения, позволяя ему не формулировать явно точные ограничения. Вот почему плодотворный обмен идеями между теорией нечетких множеств и классическим программированием может явиться значительным шагом к созданию новых методов.
Стандартная задача нечеткого математического программирования формулируется обычно как задача максимизации (или минимизации) заданной функции на заданном множестве допустимых альтернатив, которое описывается системой равенств или неравенств. Например:
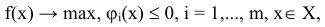
где 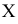 — заданное множество альтернатив,
— заданное множество альтернатив, 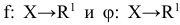 — заданные функции.
— заданные функции.
При моделировании в нечеткой форме реальных задач принятия решений в распоряжении исследователя-математика могут оказаться лишь нечеткие описания функции  и
и 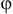 , параметров, от которых зависят эти функции, да и самого множества
, параметров, от которых зависят эти функции, да и самого множества 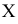 . Таким образом, задача стандартного математического программирования превратится в задачу нечеткого математического программирования.
. Таким образом, задача стандартного математического программирования превратится в задачу нечеткого математического программирования.
Формы нечеткого описания исходной информации в задачах принятия решений могут быть различными; отсюда и различия в математических формулировках соответствующих задач нечеткого математического программирования.
Перечислим некоторые из таких постановок [8а].
Задача 1. Максимизация заданной обычной функции 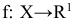 на заданном нечетком множестве допустимых альтернатив
на заданном нечетком множестве допустимых альтернатив 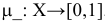 .
.
Задача 2. Нечеткий вариант стандартной задачи математического программирования. Пусть определена следующая задача математического программирования:
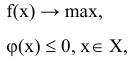
Нечеткий вариант этой задачи получается, если «смягчить» ограничения, т.е. допустить возможность их нарушения с той или иной степенью. Кроме того, вместо максимизации функции 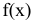 можно стремиться к достижению некоторого заданного значения этой функции, причем различным отклонениям значения функции от этой величины приписывать различные степени допустимости.
можно стремиться к достижению некоторого заданного значения этой функции, причем различным отклонениям значения функции от этой величины приписывать различные степени допустимости.
Задача 3. Нечетко описана «максимизируемая » функция, т.е. задано отображение 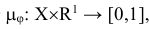 , где
, где 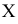 — универсальное множество альтернатив,
— универсальное множество альтернатив, 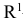 — числовая ось.
— числовая ось.
В этом случае функция 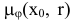 при каждом фиксированном
при каждом фиксированном 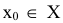 представляет собой нечеткое описание оценки результата выбора альтернативы
представляет собой нечеткое описание оценки результата выбора альтернативы 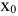 (нечеткую оценку альтернативы
(нечеткую оценку альтернативы 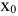 ) или нечетко известную реакцию управляемой системы на управление
) или нечетко известную реакцию управляемой системы на управление 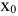 . Задано также нечеткое множество допустимых альтернатив
. Задано также нечеткое множество допустимых альтернатив 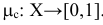
Задача 4. Заданы обычная максимизируемая функция 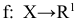 и система ограничений вида
и система ограничений вида 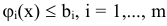 , причем параметры в описаниях функций
, причем параметры в описаниях функций 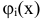 заданы в форме нечетких множеств.
заданы в форме нечетких множеств.
Задача 5. Нечетко описаны как параметры функций, определяющих ограничения задачи, так и самой максимизируемой функции.
Рассмотрим, например подробнее задачу линейного программирования с нечёткими коэффициентами. Нечеткость в постановке задачи математического программирования может содержаться как в описании множества альтернатив, так и в описании целевой функции.
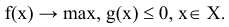
На практике часто сталкиваются с применением точной теории оптимизации к неточным моделям, где нет оснований писать точно определенные числа и где слишком часто появляются трудности вычислительного характера при описании больших систем.
Нечеткую обстановку можно рассматривать как множество 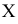 альтернатив вместе с его нечеткими подмножествами, представляющими собой нечетко сформулированные критерии (цели и ограничения), т.е. как систему (
альтернатив вместе с его нечеткими подмножествами, представляющими собой нечетко сформулированные критерии (цели и ограничения), т.е. как систему (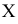 ,
, 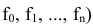 . Принять во внимание по возможности все критерии в такой задаче означает построить функцию
. Принять во внимание по возможности все критерии в такой задаче означает построить функцию
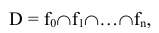
в которую цели и ограничения входят одинаковым образом.
Решение можно определить как нечеткое подмножество универсального множества альтернатив. Оптимум соответствует той области 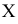 , элементы которой максимизируют
, элементы которой максимизируют 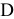 . Это и есть случай нечеткого математического программирования.
. Это и есть случай нечеткого математического программирования.
Очевидно, неразумно в реальных ситуациях проводить резкую границу для множества допустимых альтернатив, поскольку может случится так, что распределения, лежащие за этой границей, дадут эффект, превышающий меньшую желательность для лица принимающего решения.
Например, ясно, что при несовместных распределениях эта область пустая. В этом случае налицо необходимость модификации ограничений. Желательно выяснить, как изменить ограничения задачи, чтобы появились допустимые решения, и задача стала разрешимой.
В таких случаях представляется целесообразным вводить нечеткое множество допустимых элементов и, следовательно, рассматривать проблему как задачу НМП с применением подхода, дающего человеку больше свободы в использовании его субъективных представлений о ситуации.
Формы нечеткого описания исходной информации в задачах принятия решений могут быть различными; отсюда и различия в математических формулировках соответствующих задач НМП.
Нечеткий вариант стандартной задачи математического программирования получается, если «смягчить» ограничения, т.е. допустить возможность их нарушения с той или иной степенью. Кроме того, вместо максимизации целевой функции 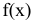 можно стремиться к достижению некоторого заданного ее значения, причем различным отклонениям значения
можно стремиться к достижению некоторого заданного ее значения, причем различным отклонениям значения 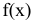 от этой величины приписывать различные степени допустимости (например, чем больше отклонение, тем меньше степень его допустимости).
от этой величины приписывать различные степени допустимости (например, чем больше отклонение, тем меньше степень его допустимости).
Пусть 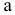 — заданная величина функции цели
— заданная величина функции цели 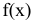 , достижение которой считается достаточным для выполнения цели принятия решений, и пусть имеется пороговый уровень
, достижение которой считается достаточным для выполнения цели принятия решений, и пусть имеется пороговый уровень 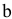 такой, что неравенство
такой, что неравенство 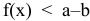 означает сильное нарушение неравенства
означает сильное нарушение неравенства 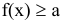 . Тогда функцию принадлежности для нечеткой функции цели можно определить следующим образом:
. Тогда функцию принадлежности для нечеткой функции цели можно определить следующим образом:

где 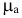 — функция принадлежности, описывающая степени выполнения соответствующего неравенства с точки зрения лица, принимающего решения.
— функция принадлежности, описывающая степени выполнения соответствующего неравенства с точки зрения лица, принимающего решения.
Аналогично определяется функция принадлежности 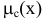 для нечетких ограничений. В результате исходная задача оказывается сформулированной в форме задачи выполнения нечетко определенной цели, к которой применим подход Беллмана-Заде (8.2) [86].
для нечетких ограничений. В результате исходная задача оказывается сформулированной в форме задачи выполнения нечетко определенной цели, к которой применим подход Беллмана-Заде (8.2) [86].
При моделировании ситуации в форме задачи линейного программирования
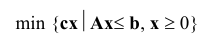
о коэффициентах 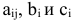 известно лишь то, что они находятся в некотором множестве, отражающем все реальные возможности.
известно лишь то, что они находятся в некотором множестве, отражающем все реальные возможности.
В некоторых случаях точное описанное множество ограничений (допустимых альтернатив) может оказаться лишь приближением реальности в том смысле, что в реальной задаче альтернативы вне множества ограничений могут не допустимыми, а лишь в той или иной степени менее желательными для лица, принимающего решения, чем альтернативы внутри этого множества.
Рассмотрим задачу нахождения минимума на заданной области. Пусть задана область вида:
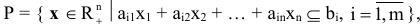
где 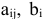 — нечеткие подмножества множества
— нечеткие подмножества множества 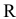 , а бинарная операция «+» обозначает сложение нечетких множеств.
, а бинарная операция «+» обозначает сложение нечетких множеств.
Требуется найти
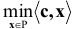
на заданной области.
Коэффициент при каждой переменной в ограничениях можно считать функцией полезности, определенной на числовой оси.
Можно считать, что эти коэффициенты дают субъективную оценку различных возможностей, включая, таким образом, другие, не определенные ограничения.
Сведём решение исходной задачи к решению ряда задач линейного программирования. Для этого введём дискретные 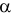 -уровни [8в, 8г]. В результате нечёткие ограничения принимают следующий интервальный вид:
-уровни [8в, 8г]. В результате нечёткие ограничения принимают следующий интервальный вид:
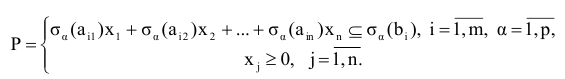
Таким образом, мы перешли от нечётких множеств к чётко определённым и теперь, зная, что 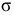 — обычный интервал, можем записать нашу задачу в следующем виде (случай 2×2):
— обычный интервал, можем записать нашу задачу в следующем виде (случай 2×2):
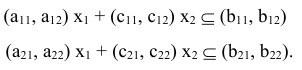
Теперь, чтобы привести задачу к виду обычной задаче линейного программирования, нам достаточно записать неравенства отдельно по левому и правому краям интервалов, с учётом знаков неравенства. Т.е., мы приведём систему к следующему виду:
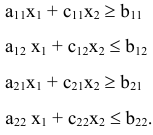
С помощью несложных преобразований мы перешли от задачи с нечёткими коэффициентами к задаче линейного программирования с чёткими коэффициентами , при этом количество ограничений увеличилось в два раза и полученную задачу мы можем решить симплексным методом.
Таким образом, из рассмотренного примера явно просматривается алгоритм решения задачи с нечеткими коэффициентами. Следуя ходу рассуждений в данном примере, составим алгоритм решения задачи. Он имеет вид:

Как видим, исходная задача НМП представляется в виде совокупности обычных задач линейного программирования на всевозможных множествах уровня множества допустимых альтернатив. Если альтернатива 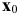 есть решение задачи
есть решение задачи 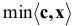 на множестве уровня
на множестве уровня 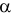 , то можно считать что число
, то можно считать что число 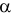 есть степень принадлежности альтернативы
есть степень принадлежности альтернативы 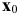 нечеткому множеству решений исходной задачи. Перебрав, таким образом, всевозможные значения
нечеткому множеству решений исходной задачи. Перебрав, таким образом, всевозможные значения 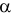 , получаем функцию принадлежности нечеткого решения.
, получаем функцию принадлежности нечеткого решения.
Если же и компоненты целевой функции 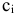 являются нечеткими, то необходимо выбирать для каждого уровня а соответствующие границы множеств
являются нечеткими, то необходимо выбирать для каждого уровня а соответствующие границы множеств 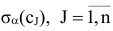 в соответствии с правилами интервальной арифметики, минимизируя предварительно таким образом
в соответствии с правилами интервальной арифметики, минимизируя предварительно таким образом 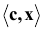 .
.
Из данного примера видно, что за гибкость приходится платить ценой увеличения размерности задачи. Фактически исходная задача с ограничениями по включению преобразуется в задачу с ограничениями в виде неравенств, с которыми легко обращаться; при этом такая цена не слишком высока, поскольку сохраняется возможность использования хорошо разработанных классических методов.

