Оглавление:



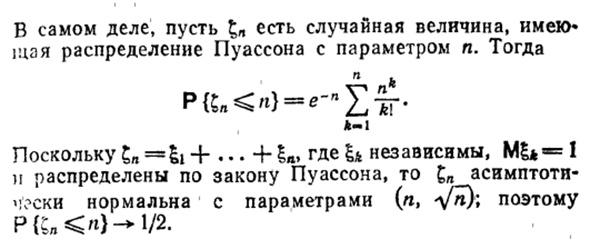

Применения центральной предельной теоремы
- Центральное приложение Предельная теорема Доказанная выше предельная теорема имеет теоретическое и прикладное значение. Главное в условиях этих теорем состоит в том, что в сумме £ n = • = ^ 1 + ^ 2 + ••• каждый член мал Случайный вклад в общую сумму. В частности, это подтверждается тем фактом, что Dc * / D £ n-►О равномерно по I ^ k ^ n при η-> oo.
- В приложениях часто используется предположение, что случайные величины, встречающиеся в вычислениях, приблизительно нормально распределены. Предполагая нормальность, строится так называемая теория ошибок измерения. Эта теория изучает, как учитывать случайные ошибки при измерении определенных параметров в экспериментах.
Например, в антропологии обработка измерений параметров человека также основана на предположении о нормальном распределении этих параметров. Людмила Фирмаль
Основой для предположения о здоровье в этих случаях являются большие статистические данные, накопленные во время измерения. Поскольку на значения параметров реальных явлений часто влияют многие случайные независимые факторы, каждый из которых имеет небольшой эффект и в целом имеет какой-то конкретный эффект, центральная предельная теорема подразумевает, что Дайте теоретическое обоснование.
Ироничное утверждение статистики на эту тему известно как: «Опытные люди убеждены в правильности метода нормального распределения, потому что они считают, что это математическая теорема. Эта пословица гласит, что математическая теория сама по себе является не реальным явлением, а только математической моделью».
Помните, что это основано, поэтому в теории вероятностей и общих математических приложениях вы всегда должны помнить о здравом смысле и всегда рассматривать правильную модель, которая правильно отражает соответствующее явление. Рассмотрим некоторые приложения центральной предельной теоремы. Используйте следующую терминологию:
- Последовательность случайных величин пn An и Bn limPj-Cp ^ <Λ = φ (g), (12) л-юо к дн) Далее мы говорим, что случайная величина „„ асимптотически нормальна по параметрам (яя, Bn) или просто асимптотически нормальна по (яя, Bn). P {U ~ nAn <*} ~ Φ (x). Пример 1. Ошибка измерения. Измерение значения дает приблизительное значение. Ошибка 6 = £ -а может быть выражена как сумма двух ошибок. Первый I-M £ называется случайной ошибкой, а второй — систематической ошибкой.
Случайная ошибка 6 имеет математическое ожидание M6 = 0. D6 = 0 (an, aUn) асимптотически нормальна. Следовательно, когда η велико (g, a / Vy), оно асимптотически нормально, eVn / tt, \ e ~ du (13) Из (13), с помощью любого грубого метода измерения, мы можем формально сделать вывод, что если n большое, мы получим любой точный результат.
Хороший метод измерения не должен иметь системы ошибок, поэтому предположим, что M = a. Людмила Фирмаль
Это противоречит здравому смыслу. В чем здесь проблема? Очевидно, что измерения грубым методом не соответствуют модели, основанной на основании, из которого было получено уравнение (13). И на самом деле, большие подразделения измерительных инструментов не могут гарантировать отсутствие систематических ошибок.
Во многих случаях предполагается, что каждое измерение h имеет нормальное распределение параметров (a, o), чтобы отвлечь внимание от ошибок округления. Во-вторых, (13) точно меняется от приближенного уравнения. Пример 2. Логнормальное распределение. В антропологии рост или вес человека определенного возраста и пола обычно считаются случайной величиной с нормальным распределением.
Однако часто можно предположить, что логарифмы этих параметров имеют нормальное распределение по гораздо более важным причинам. Говорят, что случайная величина m | £ = log r | имеет нормальное распределение, а x \ имеет логнормальное распределение или, короче говоря, логнормальное распределение. Логнормальность роста и веса может дать некоторое теоретическое обоснование.
Фактически, например, вес получается в результате воздействия многих независимых причин, но эти причины не являются аддитивными к весу, а мультипликативными, то есть мультипликативными. Л = Л1Л2 ••• Л *, где m | / — почти одна независимая случайная величина. В этом случае L log A = £ log A | Логри имеет нормальное распределение в пределе из-за центральной предельной теоремы.
Пример 3. Используя центральную предельную теорему, вы можете: Но для доказательства чисто аналитических фактов. Мы, например, н к «» • «■ Etg-t- * О Фактически, предположим, что у вас есть случайная величина с распределением Пуассона с параметром n. + … (потому что £ * здесь не зависит) M £ * = 1 Он распределен по закону Пуассона и асимптотически нормален с параметрами (n, n / n), поэтому P {$ {<*} — II / 2.
Смотрите также:
Решение задач по математической статистике
| Центральная предельная теорема для одинаково распределенных независимых слагаемых | Определение и простейшие свойства |
| Теорема Ляпунова | Формула обращения |
Если вам потребуется заказать решение математической статистики вы всегда можете написать мне в whatsapp.

