Оглавление:


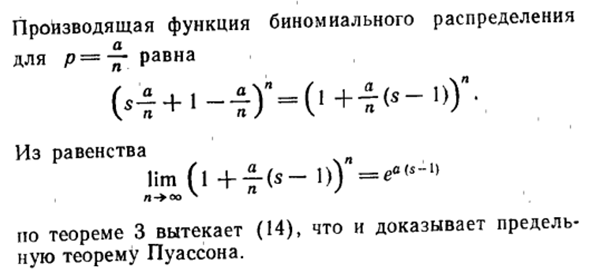

Теорема непрерывности
- Теорема о непрерывности Докажем, что соответствие между законом распределения {pn} и производящей функцией (3) не только один к одному, но также один к одному. и Теорема 3. oo Доказательство. Предположим, что lim = pp. GU е> 0, и на правой стороне неравенства OO fe-0 Jk-0 к N fe-0
- Выберите N так, чтобы sN / (1- $) r0. Тогда fg (s) -qp (s) | r0, что доказывает необходимость. Докажи, что этого достаточно. Выберите сходящуюся подпоследовательность из ограниченной последовательности 0 Выберите сходящуюся подпоследовательность p ^ -> p {и т. Д.
Из ограниченной последовательности O ^ / ^^ l. Людмила Фирмаль
- Вне последовательности К. И n (2. D p (3.1) Pn * P> Pn » (1.2) n (2.2) (3.2) RP> RP »RP • ‘* • ya.p) n (2,3) n (3.3) Pn> P / x »Pn 9 ••• Выберите подпоследовательность диагональной сходимости pjf’r>, которая сходится к pn для любого π. Предположим, что последовательность ft хотя бы для одного η? Не сходится к RP.
Затем вы можете выбрать две подпоследовательности, которые сходятся к разным пределам последовательности ffpпуpjp P * n. Согласно первой части теоремы — + Φ ‘(*) = Z p \ sn «= = Pn Sn. Так как н н Условие Т * е ‘lim = G-> OO Замечания. Пример yr (s) = sr-> 0 Генерирующая функция биномиального распределения (Hg + ‘- £) «= (‘ + m <* — ‘>)» — Из равенства lim (l + — (s-])) = = ea <5- » n- + oo \ L /
Теорема 3 продолжается (14), доказывая предельную теорему Пуассона. Людмила Фирмаль
Смотрите также:
Решение задач по математической статистике
| Факториальные моменты | Ветвящиеся процессы |
| Мультипликативное свойство | Определение и простейшие свойства характеристических функций |
Если вам потребуется помощь по математической статистике вы всегда можете написать мне в whatsapp.

