Оглавление:





Кривые линии и их проекции
- Кривая Липни и ее проекция 1. Плоская кривая. Все точки плоской кривой линии лежат в одной плоскости, определенной тремя точками плоской кривой, которые не находятся на одной линии. Наиболее распространенные плоские кривые на практике — это квадратичные кривые 1: круги, эллипсы, параболы, гиперболы и различные регулярные кривые, такие как синусоиды, циклоиды и архимедовы спирали.
- Основываясь на свойствах параллельной проекции, вы можете определить свойства кривых, которые сохраняются в проекции. Следовательно, в общем случае секущий и тангенс кривой проецируются на секущий и ее проецируемый тангенс, соответственно, но число пересечений между секущей и кривой2 сохраняется.
Точка бесконечности кривой проецируется на точку бесконечности проекции. Людмила Фирмаль
Если вы сохраните эти свойства кривой во время параллельной проекции, вы увидите, что круг и эллипс проецируются на эллипс, парабола проецируется на параболу, а гипербола проецируется на гиперболу. Кривая называется гладкой, если каждая из ее точек имеет уникальный тангенс t, который непрерывно изменяется от точки к точке.
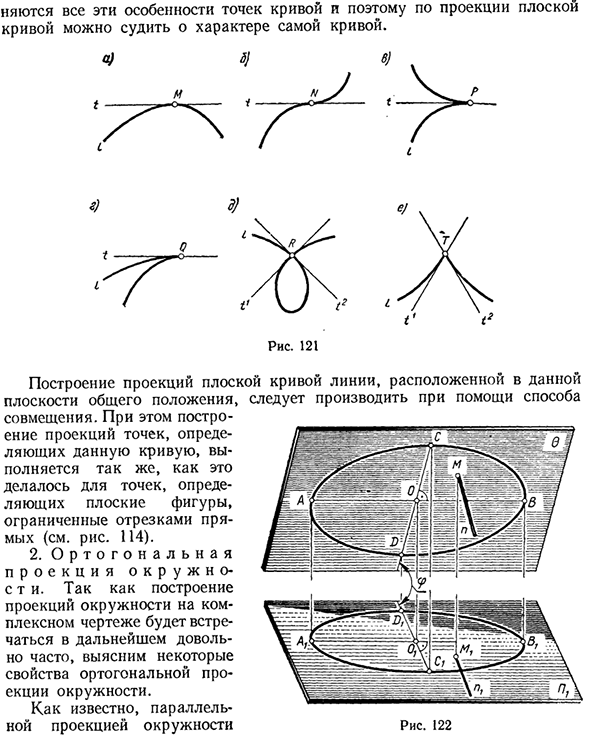
Кривые точки можно разделить на нормальные и специальные. На рисунке 121. a показана нормальная точка Mt a на рисунке 121. 121, b, c, d, e, e — несколько особенностей (точка перегиба N, точка возврата первого типа P и точка второго типа Q, узел R и точка останова «D»). Кривая, определенная в декартовых координатах одним алгебраическим уравнением, называется алгеброй, а порядок уравнения — порядком кривой.
Порядок алгебраической кривой определяет максимальное количество пересечений с прямой. Таким образом, квадратичная кривая пересекает любую линию не более чем с двумя точками. 2 Это означает, что порядок плоских алгебраических кривых сохраняется при параллельной проекции. Поскольку ни одна из этих особенностей точки кривой не существует, проекция плоской кривой может определить природу самой кривой.
А потом. 4 S1 м — Рисунок 121 Проецирование плоской кривой линии в определенной плоскости в общем месте должно быть выполнено с использованием метода выравнивания. В этом случае построение проекции точек, которые определяют эту кривую, выполняется так же, как и точки, которые определяют плоскую фигуру, разделенную отрезками (см. Рис. 114). 2.
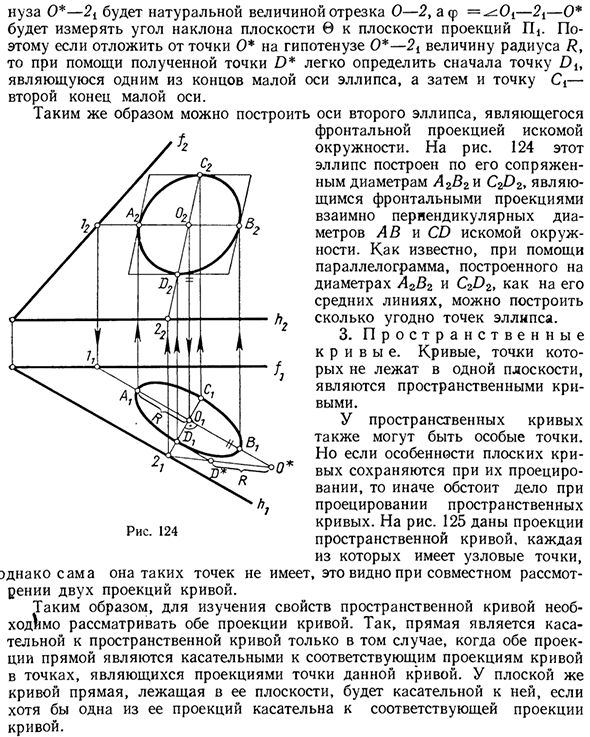
Ортографическая проекция круга. Поскольку построение круговых проекций на сложных чертежах будет очень частым в будущем, мы найдем некоторые характеристики ортогональных круговых проекций. Как известно, параллельная проекция окружности 122 Кривая называется эллипсом.
Поскольку ортогональная проекция является частным случаем параллельной проекции, эллипс 0 \ получается путем проецирования круга O на плоскость с общим положением 0 (рис. 122) перпендикулярно плоскости. В круге нарисуйте два диаметра AB и CD, которые ортогональны друг другу.
Кроме того, AB проходит по прямой в плоскости 0, а диаметр CD проходит по прямой с максимальным наклоном этой плоскости относительно плоскости проекции G1. Затем диаметр AB проецируется на диаметр эллипса, равный диаметру круга. То есть AB = AXBV, а диаметр CD проецируется на диаметр эллипса CjDj.
Угол, образованный этими диаметрами, является линейным углом с двугранным углом от плоскости 0 к плоскости Pi, и чтобы обозначить его через <p, мы получим CiD = = CD cosφ хорду к другому диаметру Это свойство сохраняется при параллельном проецировании, поэтому диаметры AXBX и C, D являются диаметром сопряженного эллипса.
Но с другой стороны, эти диаметры перпендикулярны друг другу. Поскольку они представляют собой проекции диаметров, перпендикулярных друг другу, один из них параллелен плоскости проекции, поэтому он является осью эллипса, а AXB {является большой осью, а C \ DX является малой осью.
Вот так Большая ось эллипса, которая является ортогональной проекцией круга в конкретной плоскости 0, параллельна линейной проекции уровня этой плоскости и равна диаметру окружности, а малая ось является проекцией прямой линии с максимальным наклоном плоскости 0. Плоскость проекции параллельна и равна диаметру круга, умноженному на косинус угла наклона плоскости.
Если большая ось эллипса равна 2a, малая ось равна 2b, а диаметр круга равен d, 2a = d \ 2b = d cos y. Вы можете добавить другой знак, чтобы определить направление оси эллипса. Это ортографическая проекция круга. Если нарисовать прямую линию n перпендикулярно плоскости 0 (рис. 122), такая линия перпендикулярна прямой линии 0. В частности, он будет перпендикулярен диаметру AB || P |. Поэтому его ортографическая проекция n!
Прямая линия на плоскости ГЦ перпендикулярна проекции AtBi диаметром AB. То есть проекция, перпендикулярная плоскости 0, параллельна малой оси эллипса. так себе И обратная позиция: Малая ось эллипса, являющаяся ортографической проекцией круга, Проекция перпендикуляров на любую плоскость 0. Рассмотрим построение сложной круговой проекции.
Они могут быть построены в общем виде путем объединения плоскости круга с плоскостью уровня и построения проекции отдельных точек круга. Однако рассмотрим пример построения круговой проекции на основе ортографических свойств. Пример 1. Нарисуйте круг с радиусом R с центром в точке O на плоскости 2, которая выступает вперед (Рисунок 123).
- В этом случае передняя проекция круга представляет собой отрезок с длиной прямой линии 2R, а горизонтальная проекция представляет собой эллипс. Большая ось C \ DX этого эллипса, согласно предыдущему примеру, параллельна горизонтальной проекции горизонтальной плоскости (в данном случае прямой линии, выступающей вперед) 2 и равна диаметру окружности 2R.
Короткая ось AiBi параллельна горизонтальной проекции прямой линии с максимальным наклоном плоскости 2 (в данном случае передней) и равна 2R-cos <стр.Благодаря осям эллипса AtBt, C и O вы можете легко построить столько точек, сколько захотите, используя две концентрические окружности, построенные на этих осях, например диаметры.
Где f — угол наклона плоскости 2 относительно плоскости проекции ITj. Людмила Фирмаль
Пример 2. Создайте круг с радиусом R с центром в точке O (02) на плоскости 0 (hxf) в общем месте (Рисунок 124). Сначала найдите центр O оси эллипса, большой A ^ B ^ и малый CjDj. Это горизонтальная проекция желаемого круга. Для этого нарисуйте плоскость с горизонталью 0–1 и прямой линией с максимальным наклоном O — 2 относительно плоскости проекции U.
Тогда вы можете легко найти центр Ox и длинную ось AXBX в горизонтальной горизонтальной проекции O. С 2 р Малая ось CiD, эллипс, находится на горизонтальной проекции прямой линии с максимальным наклоном O — 2. Чтобы определить его длину, постройте прямоугольный треугольник O, -O * -2, если одна ветвь является сегментом Oi — 2it, а другая ветвь является превышением точки O относительно точки 2, гипотеза.
Ортогонально к параллели Шум O * -2t — это естественный размер сегмента O-2, acr = -2, а -O * измеряет угол наклона плоскости относительно плоскости проекции Ot. Таким образом, если точка O * на гипотенузе 0 откладывается до значения радиуса R, результирующая точка D * используется, чтобы сначала определить точку Dit, один из концов короткой оси эллипса, а затем короткую.
Нетрудно определить вторую точку C4 оси. Точно так же вы можете создать вторую ось эллипса. Фронтальная проекция нужного круга. Рисунок 124. Этот эллипс состоит из сопряженных диаметров A2B2 и C2D2. Эти сопряженные диаметры являются фронтальными проекциями диаметров AB и CD, перпендикулярных друг другу желаемой окружности.
Как вы знаете, параллелограмм, построенный на диаметрах A2B2 и C2D2, может быть использован для построения любого числа эллипсов на средней линии. 3. Пространственная кривая. Кривые, точки которых не находятся на одной плоскости, являются пространственными кривыми. Пространственные кривые также могут иметь особенности.
Однако ситуация при проецировании пространственной кривой иная, если характеристики плоской кривой сохраняются во время проецирования. Рис. 125. Учитывая проекцию пространственной кривой, каждая проекция имеет узел, но сама по себе такой точки не существует. Это видно по совместному рассмотрению двух проекций кривой.
Поэтому, чтобы изучить характеристики пространственной кривой, необходимо рассмотреть обе проекции кривой. Следовательно, линия касается кривой пространства только в том случае, если обе проекции линии касаются соответствующей проекции кривой в точке, которая является проекцией указанной точки кривой.
Для плоских кривых прямая линия в этой плоскости является касательной, если хотя бы одна из ее проекций касается соответствующей проекции кривой. Рис. 124 Затем определите длину дуги с учетом линеаризации пространственной кривой (рис. 125). Во-первых, прямая линия AtB {горизонтальная проекция дуги A {Bt этой кривой. Для этого разбейте эту дугу на части. От аккордов, стягивая их вместе, эти аккорды располагаются в порядке на горизонте.
Далее прямая линия, параллельная линии связи, проводится через полученные точки деления. Кроме того, отложите относительную высоту соответствующих точек на кривой пространства. Тогда ломаная Ai-J2 —— 72-B2 Дает приблизительную длину заданной дуги A после линеаризации в отрезок прямой.
Легко видеть, что уменьшение линеаризации дуги пространственной кривой основано на построении натурального размера сегментов методом прямоугольного треугольника. 4. Из пространственных кривых наиболее распространенной на самом деле является цилиндрическая спираль.
Если точка A движется равномерно вдоль прямой линии и равномерно вращается вокруг своей параллельной оси, то прямая линия представляет поверхность цилиндра, а точка A представляет пространственную кривую, называемую цилиндрической спиралью.К. Для высоты L расстояние, на которое точка А поднимается за один полный оборот, называется шагом спирали.
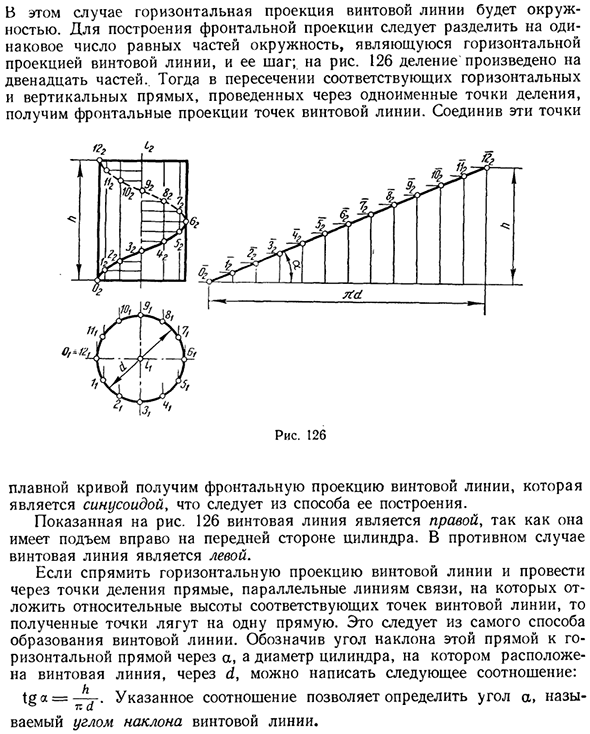
На фиг.126 показана структура спирального выступа, ось которого i перпендикулярна горизонтальной плоскости выступа. В этом случае горизонтальная проекция спирали представляет собой круг. Чтобы создать фронтальную проекцию, необходимо разделить круг, который является горизонтальной проекцией спирали, и ее шагом на одинаковое количество равных частей.
Рисунок 126 разделен на 12 частей. Затем получают фронтальную проекцию спиральной точки на пересечении соответствующих горизонтальных и вертикальных линий через одну и ту же точку разделения. Соедините эти точки Если вы рисуете плавную кривую, вы получаете фронтальную проекцию спирали. Это синусоида, полученная в результате метода строительства.
Спираль 126 показана правильно, потому что она поднимается вправо перед цилиндром. В противном случае спираль остается. Если вы проведете прямую линию, параллельную линии связи, через точку разделения, где горизонтальная проекция спирали выпрямлена, а относительная высота соответствующей точки спирали снята, результирующие точки окажутся на одной прямой линии.
Это происходит от самого способа формирования спирали. Учитывая угол наклона этой линии относительно горизонтальной линии, проходящей через a, и диаметр цилиндра, где расположена спираль, проходящая через d, мы можем записать следующее соотношение: тга = — ^ -. В зависимости от указанного соотношения вы можете определить угол а, называемый углом спирали.
Смотрите также:
Примеры решения задач по начертательной геометрии
| Способ вращения вокруг прямой уровня (способ совмещения) | Образование, задание и изображение поверхностей |
| Способ дополнительного проецирования | Взаимное пересечение многогранников |

