Прямые наибольшего уклона плоскости

Прямые наибольшего уклона плоскости

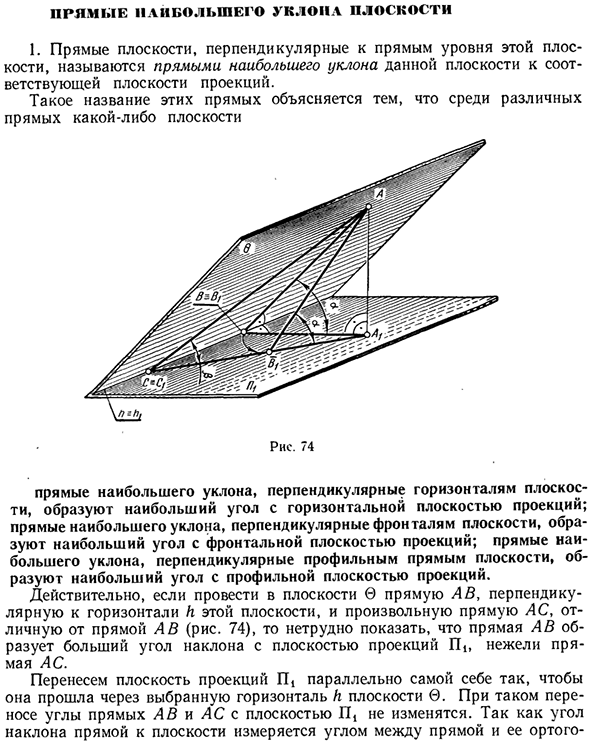
• Прямой самый простой склон 1. Прямая плоскость, перпендикулярная линии уровня этой плоскости, называется прямой с максимальным наклоном плоскости относительно соответствующей плоскости проекции. Названия этих линий — это различные линии на плоскости. Рис. 74

• Прямая линия с максимальным наклоном, перпендикулярным горизонтальной плоскости, образует максимальный угол с горизонтальной плоскостью проекции. Прямая линия с максимальным наклоном, перпендикулярным передней части плоскости, образует максимальный угол с передней частью проекции.

Прямая линия с максимальным наклоном, перпендикулярным линии профиля плоскости, образует максимальный угол с плоскостью профиля проекции. Людмила Фирмаль

Фактически, если прямая AB перпендикулярна горизонтали h этой плоскости и произвольная прямая AC (рис. 74), отличная от прямой AB, проведена в плоскости 0, прямая AB образует большой угол наклона с плоскостью проекции Pi. Прямой динамик, который легко показать. Перенести плоскость проекции P | параллельно себе так, чтобы она проходила через выбранную горизонтальную плоскость И плоскости 0.

При такой передаче угол между прямой AB и плоскостью P переменного тока не изменяется. Потому что угол наклона линии относительно плоскости измеряется углом между линией и ее ортогональной линией Спроецированные на эту плоскость, измеряют углы прямых AB и AC с плоскостью P | углы a = ^ ABAt и fl = ^ ASA {соответственно. Обозначает> 0.

Чтобы сделать это, рассмотрим Cc с двумя прямыми треугольниками, AAgB и DLL, и общей ножкой AAt. Для этих треугольников A B <L C. Это потому, что он вертикальный и A C наклонен относительно горизонтального h. Поэтому, когда вы вращаетесь вокруг плоскости рассматриваемого треугольника, AA занимает позицию A Bx в треугольнике AAfi.

Следовательно, прямая линия A плоскости 0, перпендикулярной горизонтали h, является прямой линией с максимальным уклоном относительно горизонтальной плоскости проекции. Аналогично, прямая линия в плоскости 9, перпендикулярной передней части или контуру этой плоскости, может оказаться прямой линией с наибольшим уклоном относительно передней или контурной поверхности проекции, соответственно.

Прямая линия с максимальным наклоном плоскости 0 для любой проекционной плоскости, проецируемой на эту плоскость, образует линейный угол с двугранным углом плоскости 0 с соответствующей плоскостью проекции.

• Так Измерение двугранного угла между общей плоскостью 0 и плоскостью проекции может быть сведено к измерению угла между соответствующей линией с максимальным наклоном плоскости 0 и проекцией на выбранную плоскость проекции. Прямая линия с наибольшим уклоном относительно горизонтальной плоскости проекции называется линией градиента.

Это потому, что материальные частицы на плоскости вращаются вдоль этой линии. 2. Пример. Нарисуйте линию с максимальным наклоном точки В на плоскости 0 (АуВ, С) в общем месте и нарисуйте} и и2 в горизонтальной плоскости и впереди. 75 выступов (рис. 75).

Сначала создайте линию с максимальным наклоном u1 относительно плоскости проекции ||. Людмила Фирмаль

Для этого сначала создайте горизонтальную h в плоскости ©, используя liepoint /. Поскольку прямая линия с максимальным уклоном u1 перпендикулярна горизонтальной линии в плоскости b, и эта перпендикулярность сохраняется в горизонтальной проекции, построим горизонтальную проекцию ui1 перпендикулярно проекции hlt, например, рисуя точку Bt.

Но найдите фронтальную проекцию u2 * из условия, что прямая и} принадлежит плоскости. Для этого используйте точки B и 2. Затем создайте линию с максимальным наклоном u2 относительно плоскости проекции P2. Для этого нарисуйте фронт f на плоскости 8, используя точки A и 3.

Прямая линия с максимальным наклоном u2 перпендикулярна передней части плоскости B, и эта перпендикулярность сохраняется в передней проекции, поэтому передняя проекция u22 проводится через точку B2, перпендикулярную / 2. Горизонтальная проекция и * определяются с использованием точек B и 4, выбранных в плоскости 9.

Смотрите также:

Примеры решения задач по начертательной геометрии

Взаимное пересечение многогранников	Перпендикулярность прямой и плоскости
Ортогональная проекция прямого угла	Взаимная перпендикулярность плоскостей