Ортогональная проекция прямого угла

Ортогональная проекция прямого угла

• Ортогональная проекция под прямым углом 1. Помимо вопросов технического местоположения, часто необходимо решать проблемы, которые выявляют такие проблемы, как измерение сегментов и углов и определение естественной формы плоских форм. При их решении важную роль играет условие перпендикулярности между линиями и плоскостями.

• Поэтому необходимо установить, как эти условия выполняются на интегрированном чертеже. 2. Если обе стороны любого угла и, следовательно, прямого угла, параллельны плоскости проекции, такой угол находится в плоскости, параллельной плоскости проекции, и проецируется в полный размер на эту плоскость.

Для этого нам нужно найти прямолинейную ортографическую характеристику. Людмила Фирмаль

В дополнение к этому прямой угол проецируется в натуральную величину, даже если только одна сторона параллельна плоскости проекции, или вторая сторона не должна быть перпендикулярна последней. Фактически, сторона плоскости под прямыми углами к ЛВС параллельна плоскости проекции ITi.

Поскольку проекция фигуры не изменяется во время перемещения плоскости проекции, для простоты выведения перемещайте плоскость P4 проекции параллельно себе так, чтобы она проходила через параллельную сторону самолета (Рис. 69). Далее прямая £ | C, = BC перпендикулярна прямой A при условии, что угол ЛВС является прямой.

Поэтому, основываясь на трех перпендикулярной обратной теореме, прямая B1C1 также перпендикулярна проекции AtBt. Следовательно, угол AtBfiu, который является ортогональной проекцией прямого угла ABC, также является прямым углом. Есть также позиции, противоположные рассматриваемым. То есть, если, по меньшей мере, одна сторона угла, проецируемого под прямым углом, параллельна плоскости проекции, проецируемый угол также является прямым углом.

Справедливость этого положения нетрудно установить на основе трех вертикальных теорем. Учитывая, что угол A ^ Bfit является прямой линией (см. Рис. 69), линия BC = BjCi перпендикулярна линии A (но линия BC перпендикулярна наклону AB, то есть угол ABC является прямым. 3. Здесь, если ни одна из сторон прямого угла не параллельна плоскости проекции, это указывает на то, что прямой угол не может быть спроецирован на прямой угол.

Другими словами, вам нужно показать это Рисунок 70 Рис. 69 Если ортогональная ортогональная проекция представляет собой прямой угол, то по меньшей мере одна сторона этого угла параллельна плоскости проекции. Предположим, что плоскость проекции IIj перемещается параллельно, так что она проходит через перпендикулярную вершину B ЛВС (рис. 70), а сторона AB не параллельна плоскости проекции.

• Далее мы покажем, что сторона BC должна находиться в плоскости Pi. Другими словами, сторона BC параллельна плоскости проекции. На основании трех перпендикулярных теорем проекция A {проекция BBX на стороне AB условно перпендикулярна проекции BtCt условия BC и перпендикулярна прямой BC. Затем линия BC, перпендикулярная линиям AB и AxBlt, перпендикулярна плоскости проекции ABA и определяется этими линиями.

Это потому, что прямая BC имеет общую точку B = Bt с плоскостью II! 4. Вертикальное условие пересекающейся прямой линии сводится к вертикальному условию пересекающейся прямой, которое проходит через любую точку пространства и параллельно соответствующей пересекающейся прямой линии, поэтому рассматриваемые свойства являются ортогональными.

И если она перпендикулярна плоскости ABA, а затем перпендикулярна плоскости Pi, линия BC должна быть полностью в плоскости П |. Людмила Фирмаль

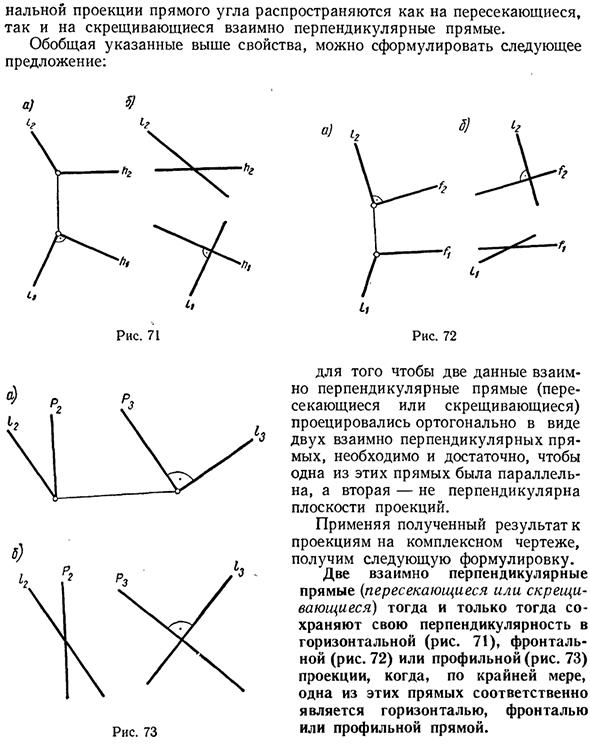
Полноугольная проекция охватывает как пересечение, так и пересечение прямых линий, перпендикулярных друг другу. Подводя итог вышеперечисленным свойствам, мы можем сформулировать следующее утверждение: а) Рисунок 72 Для проецирования двух линий данных, перпендикулярных друг другу (пересекающихся или пересекающихся).

По вертикали в форме двух линий, перпендикулярных друг другу, одна из этих линий параллельна, а вторая линия на плоскости проекции Не должно быть вертикальным. Применение результата к сложной проекции чертежа приводит к следующей формулировке:

Две прямые линии (пересекающиеся или пересекающиеся), которые перпендикулярны друг другу, являются горизонтальными линиями (Рисунок 71), передними гранями (Рисунок 72) или профилями (Рисунок 73), каждая из которых поддерживает свою вертикальность по крайней мере с одной линией. Это горизонтальная линия, линия фронта или линия профиля. В а) час Рисунок 71 Рис. 73

Смотрите также:

Примеры решения задач по начертательной геометрии

Образование, задание и изображение поверхностей	Прямые наибольшего уклона плоскости
Взаимное пересечение многогранников	Перпендикулярность прямой и плоскости