Взаимное пересечение многогранников

Оглавление:

Взаимное пересечение многогранников

Полифон взаимное пересечение 1. Пересекающаяся линия двух многогранников, называемая переходными линиями, является пространственной пунктирной линией, которую можно разделить на две или более отдельных частей. Эти части могут быть особенно плоскими многоугольниками. Вершина пересечения многогранника — это пересечение ребра первого многогранника и ребра второго многогранника, а также пересечение ребра второго многогранника и ребра первого многогранника.

Сторона или звено линии пересечения — это отрезок, где пересекаются грани обоих многогранников. Поэтому построение вершин линии пересечения многогранника сводится к многократному решению задачи о пересечении прямой с плоскостью, а построение стороны этой линии является многократным решением задачи о пересечении двух плоскостей.

Обычно они предпочитают находить вершины линии пересечения, а их стороны находят, соединяя соответствующие вершины. Людмила Фирмаль

Кроме того, ясно, что только эти пары вершин могут быть соединены отрезками на одной и той же грани первого многогранника, а также на одной грани второго многогранника. Если рассматриваемая пара вершин хотя бы одного многогранника принадлежит разным граням, такие вершины не связны.

В большинстве случаев порядок соединения вершин линии пересечения заключается в том, что после создания вершин проблема видимости ребер ребра многогранника становится ясной, и для каждого ребра, имеющего вершину линии пересечения, существует Если видимость записана до и после пересечения, это легко определить.

Конечно, в конечном итоге отображается только край отображения каждого многогранника, который пересекает поверхность отображения другого многогранника1. При соединении вершин линии пересечения необходимо учитывать видимость ссылки. Только ссылки, которые принадлежат: В сложных случаях порядок вершинных связей определяется с помощью вспомогательной таблицы под редакцией Н. Ф. Четверухининой и соавт.

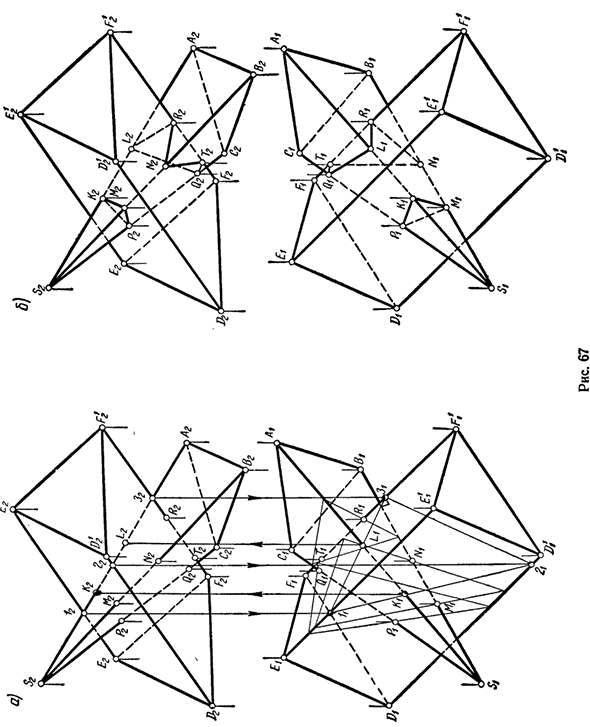
Показано в книге. , Он существует одновременно с гранями отображения как первого, так и второго многогранника. При создании линий пересечения следует учитывать, что проекции линий пересечения можно размещать только в пределах области перекрытия одной и той же проекции обоих многогранников (рис. 67).

Таким образом, по крайней мере в одной проекции, если некоторые ребра выступают за пределы области перекрытия, этот край не будет пересекать другой многогранник. Вот так Композиция вершин пересечения двух многогранников рисует на поверхности вспомогательной пунктирной линии каждого многогранника, которая конкурирует с ребрами другого многогранника, и определяет пересечение этих линий с соответствующим ребром.

Конфигурация сторон линии пересечения сводится к непрерывному соединению прямых пар найденных вершин на одной грани каждого из этих многогранников. Рассмотрим пример построения линии пересечения многогранника. Пример 1. Нарисуйте перекрестную линию между треугольной пирамидой SABC и треугольной призмой DEFD1E1Fl (Рисунок 67).

Сначала найдите пересечение края пирамиды и грани призмы. Ребра AB, BC, CA на основании пирамиды не пересекают поверхность призмы, потому что они находятся за пределами области, где выступы на этих ребрах перекрываются. Поэтому найдите пересечение ребер пирамиды S4, SB, SC и грани призмы.

Для каждого из этих краев создайте фронтальную конкурирующую линию удлинения на поверхности призмы (рис. 67, а). Людмила Фирмаль

Эти линии образуют треугольник. Следовательно, линии, конкурирующие спереди с краем SA, образуют треугольник 1-2-3. Найти точки K и L пересечения края SA и поверхности призмы на пересечении сторон 1-2 и 1-3 треугольника 1-2-3 и края SA. Определите видимость Edge SA.

Этот край пересекает плоскость DEE * Dl в точке K, пересекает плоскость EFFlE1 в точке L-, и обе эти плоскости видны в горизонтальной проекции, поэтому край SA находится на поле П и в отрезках SK и LA Я вижу это В прямой проекции поверхность DEElDl видима, а поверхность EFFlEl не видна, поэтому в поле P2 отображается край SA с сегментом SK и сегментом от точки 3 до точки, конкурирующей с точкой A.

Аналогично найдите точки M, N, P, Q на пересечении ребер SB и определите поверхность призмы и SC, а также видимость этих ребер. Здесь мы определяем пересечение края призмы и грани пирамиды. Края обоих оснований призмы не пересекают поверхность пирамиды. Это потому, что их проекции находятся за пределами области перекрытия.

Таким образом, осталось определить пересечение ребер призмы EE1, DD1, FF1 и поверхности пирамиды. Потрачено на поверхность вспомогательной пирамиды Линия, конкурирующая впереди с рассматриваемым краем призмы (Рис. 67, показана только вспомогательная линия на ребре FF1), ребра EE1 и DD1 не пересекают поверхность пирамиды, ребро FF1 пересекает поверхность пирамиды в точках R и T Я вижу что Эти ребра.

Теперь все вершины линии n Пересечения строятся и соединяют их в определенном порядке. Каждая пара вершин K, M; M, P \ P, K находится на одной грани пирамиды, и вместе они находятся на лицевой стороне призмы DEElDl. Это легко обнаружить, рассмотрев поле П (рис. 67, а). Эти вершины могут быть соединены попарно. Получите треугольник CMR, представляющий собой сечение пирамиды с гранями DEElDl (рис. 67, б).

Оставшиеся пять вершин могут быть соединены в порядке L — R — N — T — Q — L. Фактически, вершины L и R имеют общие грани S / 45 и EFF1El \, вершины R и N имеют общие грани SAB и DFFlDl \, а вершины N и T имеют общие грани SBC и DFFlDl . И вершины Q и T имеют общие грани SBC и EFFlEl, вершины T и Q имеют общие грани S-4C и EFFlEl.

Следовательно, линия пересечения состоит из двух замкнутых пунктирных линий от треугольника CMR и пространственного пятиугольника LRNTQ. Устраните проблему видимости перекрестных линий и убедитесь, что в горизонтальной проекции отображаются только ссылки KM, КР, LR и LQ, а ссылки KM, MP, NT и NR отображаются в прямой проекции.

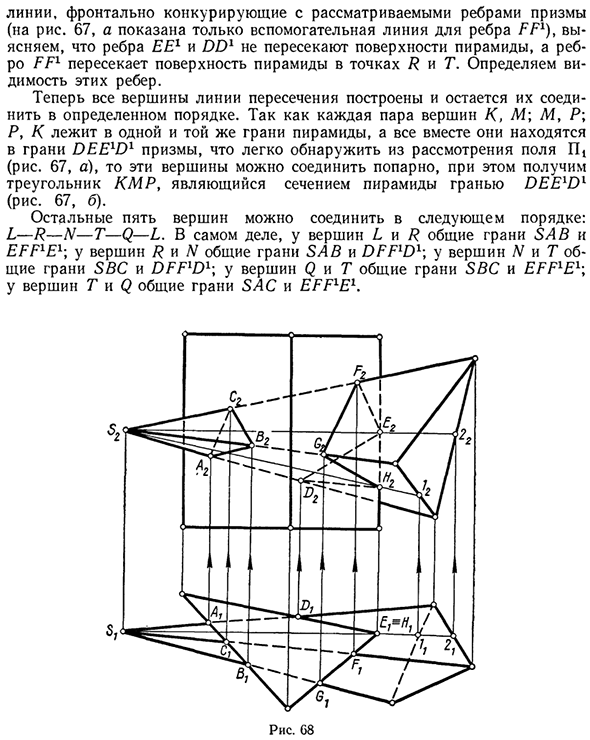
Первый и второй многогранник. При создании пересекающейся линии из двух многогранников, если проецируется хотя бы одна поверхность, необходимо использовать уменьшение этого ребра и грани многогранника до соответствующей точки и линии проекции. Пример 2. Нарисуйте линию пересечения между треугольной пирамидой и треугольной призмой.

Стороны треугольной призмы проецируются горизонтально (рис. 68). Горизонтальные проекции точек A, B, C, D, F, G на пересечении ребра пирамиды и грани призмы находятся на пересечении горизонтальных проекций, и тогда передняя проекция этих точек в соответствующем ребре передняя проекция также Будет решено.

Горизонтальная проекция точки ξ и перес на пересечении правого края призмы и плоскости пирамиды совпадает с горизонтальной проекцией самого края, а фронтальная проекция этих точек — это линия S, которая принадлежит плоскости пирамиды, которая пересекает край призмы Построен с использованием 1 и S-2.

Кривые линии и их проекции	Ортогональная проекция прямого угла
Образование, задание и изображение поверхностей	Прямые наибольшего уклона плоскости