Спирали

Спирали

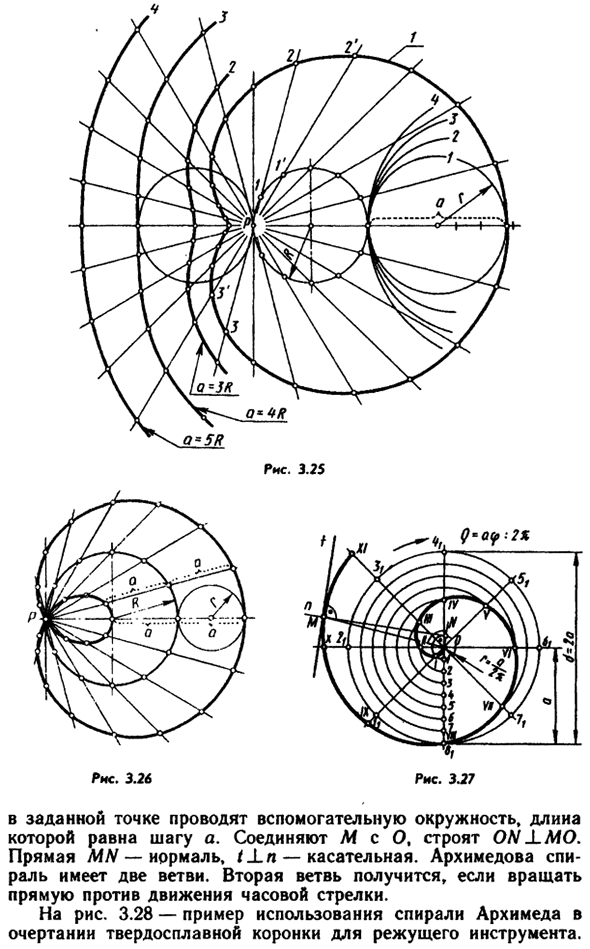
• Спираль (от Широты Спира-Изгиб, Катушка) -Плоская Бесчисленное множество кривых Точка, где каждый раунд приближается и уходит. Технически спираль Архимеда Точки, которые движутся равномерно по прямой линии Вращается вокруг фиксированной точки.

• Конкретная сборка Для шага: круг равен шагу, а его радиус Свет, проводимый таким же количеством деталей, как показано на рисунке Рисунок 3.27. Для построения касательных и нормалей 59 Рисунок 3.26 Рисунок 3.27 Нарисуйте вспомогательный круг, длина в данной точке То же, что и шаг а.

На первом луче откладывают отрезок, равный a / z, Второй 2а / п и т. Д. Людмила Фирмаль

Подключите М к О и А. Сборка с МО. Линия MN нормальная и / Xn касательная. Архимед Спираль имеет две ветви. Поверните, чтобы увидеть вторую ветку Прямо против часовой стрелки. Рисунок 3.28 — Пример использования спирали Архимеда Контур твердосплавной коронки режущего инструмента.

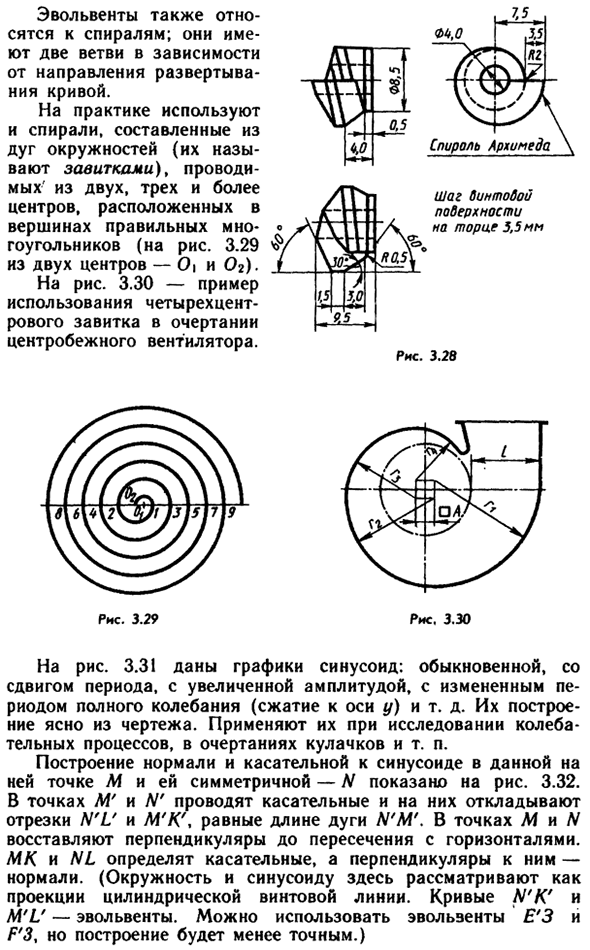
Эволютный тоже Связанные со спиралью, они Есть две ветви, от которых зависит С направления Кривая разворачивается. На самом деле использовать Спираль состоит из Дуги (те Называется локон) 2, 3 или больше Центр в Справа вверху Полигон (Рисунок 3.29) Из двух центров — 0 \ и 02).

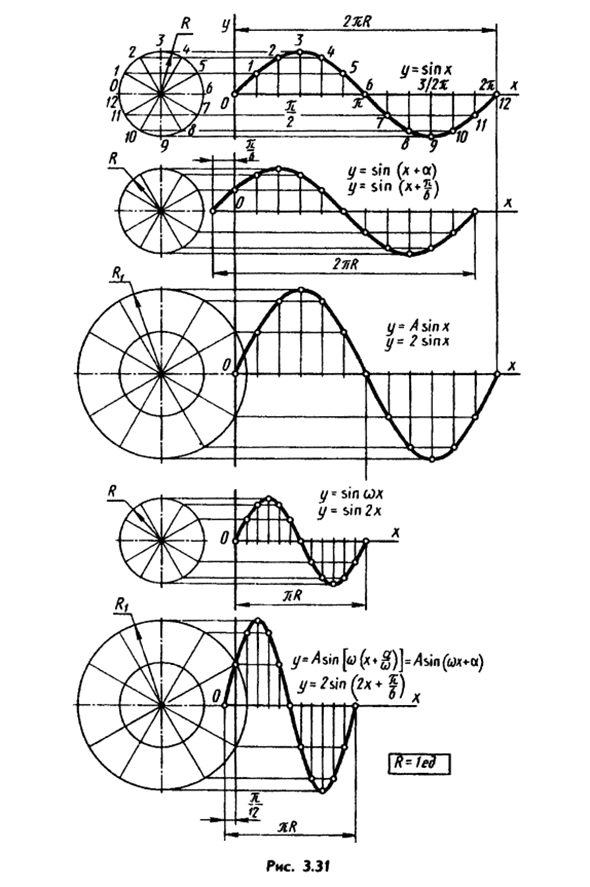
• Рисунок 3.30-Пример Использование 4 центов Контур закруглен Центробежный вентилятор. Шаг бинта поверхность 5,5 мм в конце Рисунок 3.28 Рисунок 3.29 Рис, 3,30 Рисунок 3.31. Синусоидальный график: Сдвиг периода, увеличение амплитуды, изменение Полный период вибрации (сжатие по оси Y) и т. Д. Структура понятна из чертежа.

Примените их для исследования Процесс вибрации, контур кулачка и т. Д. Это строит нормаль и тангенс синусоиды Точка M и ее симметрия -N показаны на рисунке. 3,32. В точках LH и N ‘касательные нарисованы и размещены на них Сегменты N’L ‘и LH / C’ равны длине дуги N’M \

Point M и N Восстанавливает вертикальную линию до пересечения с горизонтальной линией. Людмила Фирмаль

МК и НЛ определяют касательные и их нормали Нормальный. (Круг и синусоида здесь Проекция цилиндрической спирали. Н’К ‘кривая и M’U- эвольвентным. С эвольвентным E’Z F’3%, но структура не очень точная. )

Смотрите также:

Предмет инженерная графика

Спрямление и изгибание плоских кривых	Кривые 2-го порядка (коники)
Некоторые плоские кривые, наиболее часто встречающиеся в практике	Построение касательной и нормали к конике