Оглавление:

Прежде чем изучать готовые решения задач по ЭММ, нужно знать теорию, поэтому для вас я подготовила краткую теорию по предмету «ЭММ» и задачи с решением и примерами.
Эта страница подготовлена для школьников и студентов.
| Если что-то непонятно — вы всегда можете написать мне в WhatsApp и я вам помогу! |
Экономико-математические методы
Экономико-математические методы и модели применяют с целью отыскания наилучшего решения, то есть решения, оптимального в том или ином смысле (максимума или минимума).
На данной странице даны рекомендации по построению математических моделей и решению задач исследования операций в области: линейного программирования, сетевого планирования, регрессионного анализа, прогнозирования временных рядов, управления запасами.
В целях более эффективного усвоения учебного материала каждая тема содержит краткое теоретическое введение, подробные методические указания с описанием решения конкретных задач, варианты задач для самостоятельного решения, включая задачи повышенной сложности.
Возможно эта страница вам будет полезна:
| Предмет экономико-математические методы (ЭММ) |
Особое внимание было уделено вопросам построения математических моделей как основополагающему и наиболее творческому этапу решения задач. В связи с тем, что современное компьютерное программное обеспечение позволяет значительно упростить процесс поиска оптимальных решений, наиболее трудоемкие методы решения задач (симплекс-метод, метод потенциалов, методы оптимизации сетевых моделей) в учебном пособии рассмотрены не были.
Одноиндексные задачи линейного программирования. Построение моделей одноиндексных задач
Математическое программирование («планирование») — это раздел математики, занимающийся разработкой методов отыскания экстремальных значений функции, на аргументы которой наложены ограничения. Методы математического программирования используются в экономических, организационных, военных и др. системах для решения так называемых распределительных задач. Распределительные задачи 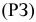 возникают в случае, когда имеющихся в наличии ресурсов не хватает для выполнения каждой из намеченных работ эффективным образом и необходимо наилучшим образом распределить ресурсы по работам в соответствии с выбранным критерием оптимальности.
возникают в случае, когда имеющихся в наличии ресурсов не хватает для выполнения каждой из намеченных работ эффективным образом и необходимо наилучшим образом распределить ресурсы по работам в соответствии с выбранным критерием оптимальности.
Линейное программирование (ЛП) является наиболее простым и лучше всего изученным разделом математического программирования. Характерные черты задач ЛП следующие:
1) показатель оптимальности 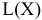 представляет собой линейную функцию от элементов решения
представляет собой линейную функцию от элементов решения 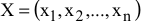 ;
;
2) ограничительные условия, налагаемые на возможные решения, имеют вид линейных равенств или неравенств.
Общая форма записи модели задачи ЛП
Целевая функция (ЦФ)
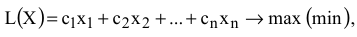
при ограничениях
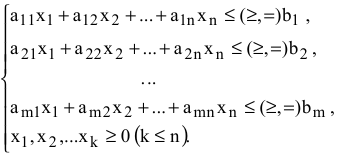
При описании реальной ситуации с помощью линейной модели следует проверять наличие у модели таких свойств, как пропорциональность и аддитивность. Пропорциональность означает, что вклад каждой переменной в ЦФ и общий объем потребления соответствующих ресурсов должен быть прямо пропорционален величине этой переменной. Например, если, продавая 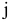 -й товар в общем случае по цене 100 рублей, фирма будет делать скидку при определенном уровне закупки до уровня цены 95 рублей, то будет отсутствовать прямая пропорциональность между доходом фирмы и величиной переменной
-й товар в общем случае по цене 100 рублей, фирма будет делать скидку при определенном уровне закупки до уровня цены 95 рублей, то будет отсутствовать прямая пропорциональность между доходом фирмы и величиной переменной 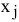 . Т.е. в разных ситуациях одна единица
. Т.е. в разных ситуациях одна единица 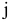 -го товара будет приносить разный доход. Аддитивность означает, что ЦФ и ограничения должны представлять собой сумму вкладов от различных переменных. Примером нарушения аддитивности служит ситуация, когда увеличение сбыта одного из конкурирующих видов продукции, производимых одной фирмой, влияет на объем реализации другого.
-го товара будет приносить разный доход. Аддитивность означает, что ЦФ и ограничения должны представлять собой сумму вкладов от различных переменных. Примером нарушения аддитивности служит ситуация, когда увеличение сбыта одного из конкурирующих видов продукции, производимых одной фирмой, влияет на объем реализации другого.
Допустимое решение — это совокупность чисел (план) 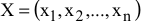 , удовлетворяющих ограничениям задачи (1.1).
, удовлетворяющих ограничениям задачи (1.1).
Оптимальное решение- это план, при котором ЦФ принимает свое максимальное (минимальное) значение.
Возможно эта страница вам будет полезна:
| Решение экономико математических методов |
Задача № 1.01
Фабрика производит два вида красок: первый — для наружных, а второй -для внутренних работ. Для производства красок используются два ингредиента: А и В. Максимально возможные суточные запасы этих ингредиентов составляют 6 и 8 т соответственно. Известны расходы А и В на 1 т соответствующих красок (табл. 1.1). Изучение рынка сбыта показало, что суточный спрос на краску 2-го вида никогда не превышает спроса на краску 1-го вида более, чем на 1 т. Кроме того, установлено, что спрос на краску 2-го вида никогда не превышает 2 т в сутки. Оптовые цены одной тонны красок равны: 3 тыс. руб. для краски 1-го вида; 2 тыс. руб. для краски 2-го вида.
Необходимо построить математическую модель, позволяющую установить, какое количество краски каждого вида надо производить, чтобы доход от реализации продукции был максимальным.
Решение:
Прежде чем построить математическую модель задачи, т.е. записать ее с помощью математических символов, необходимо четко разобраться с экономической ситуацией, описанной в условии. Для этого необходимо с точки зрения экономики, а не математики, ответить на следующие вопросы:
1) Что является искомыми величинами задачи?
2) Какова цель решения? Какой параметр задачи служит критерием эффективности (оптимальности) решения, например, прибыль, себестоимость, время и т.д. В каком направлении должно изменяться значение этого параметра (к max или к min) для достижения наилучших результатов?
3) Какие условия в отношении искомых величин и ресурсов задачи должны быть выполнены? Эти условия устанавливают, как должны соотноситься друг с другом различные параметры задачи, например, количество ресурса, затраченного при производстве, и его запас на складе; количество выпускаемой продукции и емкость склада, где она будет храниться; количество выпускаемой продукции и рыночный спрос на эту продукцию и т.д.
Только после экономического ответа на все эти вопросы можно приступать к записи этих ответов в математическом виде, т.е. к записи математической модели.
1) Искомые величины являются переменными задачи, которые как правило обозначаются малыми латинскими буквами с индексами, например, однотипные переменные удобно представлять в виде 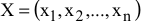 .
.
2) Цель решения записывается в виде целевой функции, обозначаемой, например, 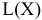 . Математическая формула ЦФ
. Математическая формула ЦФ 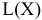 отражает способ расчета значений параметра — критерия эффективности задачи.
отражает способ расчета значений параметра — критерия эффективности задачи.
3) Условия, налагаемые на переменные и ресурсы задачи, записываются в виде системы равенств или неравенств, т.е. ограничений. Левые и правые части ограничений отражают способ получения (расчет или численные значения из условия задачи) значений тех параметров задачи, на которые были наложены соответствующие условия.
В процессе записи математической модели необходимо указывать единицы измерения переменных задачи, целевой функции и всех ограничений.
Построим модель задачи №1.01, используя описанную методику.
Переменные задачы
В задаче №1.01 требуется установить, сколько краски каждого вида надо производить. Поэтому искомыми величинами, а значит, и переменными задачи являются суточные объемы производства каждого вида красок:
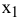 — суточный объем производства краски 1-го вида, [т краски/сутки];
— суточный объем производства краски 1-го вида, [т краски/сутки]; 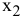 — суточный объем производства краски 2-го вида, [т краски/сутки].
— суточный объем производства краски 2-го вида, [т краски/сутки].
Целевая функция
В условии задачи №1.01 сформулирована цель — добиться максимального дохода от реализации продукции. Т.е. критерием эффективности служит параметр суточного дохода, который должен стремится к максимуму. Чтобы рассчитать величину суточного дохода от продажи красок обоих видов, необходимо знать объемы производства красок, т.е. 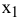 и
и 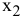 т краски в сутки, а также оптовые цены на краски 1-го и 2-го видов- согласно условию, соответственно 3 и 2 тыс. руб. за 1 т краски. Таким образом, доход от продажи суточного объема производства краски 1-го вида равен 3xj тыс. руб. в сутки, а от продажи краски 2-го вида — 2
т краски в сутки, а также оптовые цены на краски 1-го и 2-го видов- согласно условию, соответственно 3 и 2 тыс. руб. за 1 т краски. Таким образом, доход от продажи суточного объема производства краски 1-го вида равен 3xj тыс. руб. в сутки, а от продажи краски 2-го вида — 2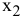 тыс. руб. в сутки. Поэтому запишем ЦФ в виде суммы дохода от продажи красок 1-го и 2-го видов (при допущении независимости объемов сбыта каждой из красок)
тыс. руб. в сутки. Поэтому запишем ЦФ в виде суммы дохода от продажи красок 1-го и 2-го видов (при допущении независимости объемов сбыта каждой из красок)
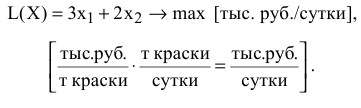
Возможные объемы производства красок 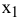 и
и 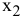 ограничиваются следующими условиями:
ограничиваются следующими условиями:
• количество ингредиентов А и В, израсходованное в течение суток на производство красок обоих видов, не может превышать суточного запаса этих ингредиентов на складе;
• согласно результатам изучения рыночного спроса суточный объем производства краски 2-го вида может превышать объем производства краски 1-го вида, но не более, чем на 1 т краски;
• объем производства краски 2-го вида не должен превышать 2 т в сутки, что также следует из результатов изучения рынков сбыта;
• объемы производства красок не могут быть отрицательными.
Таким образом, все ограничения задачи №1.01 делятся на 3 группы, обусловленные:
1) расходом ингредиентов;
2) рыночным спросом на краску;
3) неотрицательностью объемов производства.
Ограничения по расходу любого из ингредиентов имеют следующую содержательную форму записи
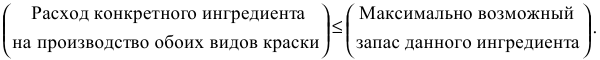
Запишем эти ограничения в математической форме.
Левая часть ограничения — это формула расчета суточного расхода конкретного ингредиента на производство красок. Так из условия известен расход ингредиента А на производство 1 т краски 1-го вида (1 т ингр. А) и 1 т краски 2-го вида (2 т ингр. А) (см. табл. 1.1). Тогда на производство 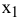 т краски 1-го вида и
т краски 1-го вида и 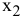 т краски 2-го вида потребуется 1
т краски 2-го вида потребуется 1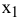 + 2
+ 2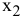 т ингр. А.
т ингр. А.
Правая часть ограничения — это величина суточного запаса ингредиента на складе, например, 6 т ингредиента А в сутки (см. табл. 1.1). Таким образом, ограничение по расходу А имеет вид
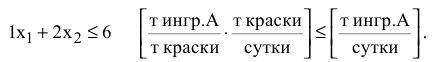
Аналогична математическая запись ограничения по расходу В
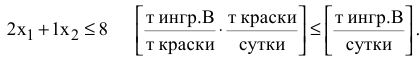
Примечание 1.1. Следует всегда проверять размерность левой и правой части каждого из ограничений, поскольку их несовпадение свидетельствует о принципиальной ошибке при составлении ограничений.
Ограничение по суточному объему производства краски 1-го вида по сравнению с объемом производства краски 2-го вида имеет
содержательную форму

и математическую форму
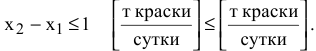
Ограничение по суточному объему производства краски 1-го вида имеет
содержательную форму
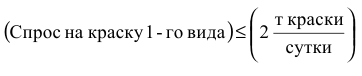
и математическую форму
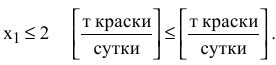
Неотрицательность объемов производства задается как
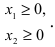
Таким образом, математическая модель этой задачи имеет вид
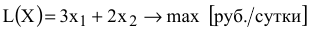
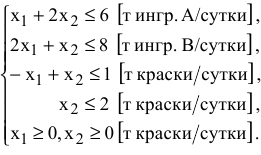
Выполнить заказ по производству 32 изделий 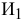 и 4 изделий
и 4 изделий 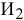 взялись бригады
взялись бригады 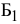 и
и 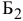 . Производительность бригады
. Производительность бригады 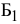 по производству изделий
по производству изделий 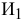 и
и 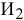 составляет соответственно 4 и 2 изделия в час, фонд рабочего времени этой бригады 9,5 ч. Производительность бригады
составляет соответственно 4 и 2 изделия в час, фонд рабочего времени этой бригады 9,5 ч. Производительность бригады 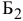 — соответственно 1 и 3 изделия в час, а ее фонд рабочего времени — 4 ч. Затраты, связанные с производством единицы изделия, для бригады
— соответственно 1 и 3 изделия в час, а ее фонд рабочего времени — 4 ч. Затраты, связанные с производством единицы изделия, для бригады 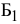 равны соответственно 9 и 20 руб., для бригады
равны соответственно 9 и 20 руб., для бригады 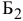 — 15 и 30 руб.
— 15 и 30 руб.
Составьте математическую модель задачи, позволяющую найти оптимальный объем выпуска изделий, обеспечивающий минимальные затраты на выполнение заказа.
Переменные задачи
Искомыми величинами в задаче являются объемы выпуска изделий. Изделия 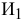 будут выпускаться двумя бригадами
будут выпускаться двумя бригадами 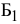 и
и 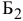 . Поэтому необходимо различать количество изделий
. Поэтому необходимо различать количество изделий 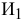 , произведенных бригадой
, произведенных бригадой 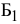 , и количество изделий
, и количество изделий 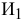 произведенных бригадой
произведенных бригадой 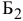 . Аналогично, объемы выпуска изделий
. Аналогично, объемы выпуска изделий 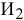 бригадой
бригадой 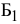 и бригадой
и бригадой 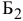 также являются различными величинами. Вследствие этого в данной задаче 4 переменные. Для удобства восприятия будем использовать двухиндексную форму записи
также являются различными величинами. Вследствие этого в данной задаче 4 переменные. Для удобства восприятия будем использовать двухиндексную форму записи 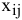 — количество изделий
— количество изделий 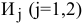 , изготавливаемых бригадой
, изготавливаемых бригадой 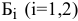 , а именно,
, а именно,

Примечание 1.2. В данной задаче нет необходимости привязываться к какому-либо временному интервалу (в задаче №1.01 была привязка к суткам), поскольку здесь требуется найти не объем выпуска за определенное время, а способ распределения известной плановой величины заказа между бригадами.
Целевая функция
Целью решения задачи является выполнение плана с минимальными затратами, т.е. критерием эффективности решения служит показатель затрат на выполнение всего заказа. Поэтому ЦФ должна быть представлена формулой расчета этих затрат. Затраты каждой бригады на производство одного изделия 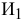 и
и 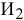 известны из условия. Таким образом, ЦФ имеет вид
известны из условия. Таким образом, ЦФ имеет вид
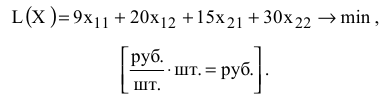
Ограничения
Возможные объемы производства изделий бригадами ограничиваются следующими условиями:
• общее количество изделий 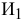 , выпущенное обеими бригадами, должно равняться 32 шт., а общее количество изделий
, выпущенное обеими бригадами, должно равняться 32 шт., а общее количество изделий 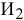 — 4 шт.;
— 4 шт.;
• время, отпущенное на работу над данным заказом, составляет для бригады 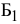 — 9,5 ч, а для бригады
— 9,5 ч, а для бригады 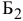 — 4 ч;
— 4 ч;
• объемы производства изделий не могут быть отрицательными величинами.
Таким образом, все ограничения задачи №1.02 делятся на 3 группы, обусловленные:
1) величиной заказа на производство изделий;
2) фондами времени, выделенными бригадам;
3) неотрицательностью объемов производства.
Для удобства составления ограничений запишем исходные данные в виде таблицы 1.2.
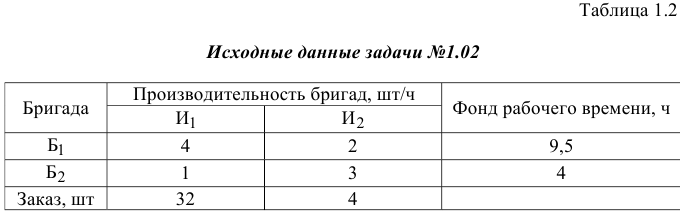
Ограничения по заказу изделий имеют следующую содержательную форму записи

Математическая форма записи имеет вид
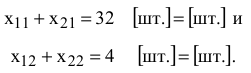
Ограничение по фондам времени имеет содержательную форму


Проблема заключается в том, что в условии задачи прямо не задано время, которое тратят бригады на выпуск одного изделия 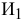 или
или 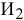 , т.е. не задана трудоемкость производства. Но имеется информация о производительности каждой бригады, т.е. о количестве производимых изделий в 1 ч. Трудоемкость Тр и производительность Пр являются обратными величинами, т.е.
, т.е. не задана трудоемкость производства. Но имеется информация о производительности каждой бригады, т.е. о количестве производимых изделий в 1 ч. Трудоемкость Тр и производительность Пр являются обратными величинами, т.е.
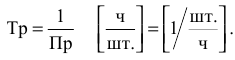
Поэтому используя табл. 1.2, получаем следующую информацию:

Запишем ограничения по фондам времени в математическом виде
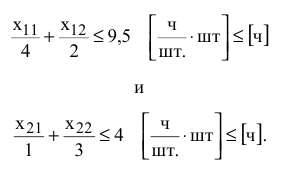
Неотрицательность объемов производства задается как
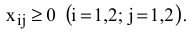
Таким образом, математическая модель этой задачи имеет вид
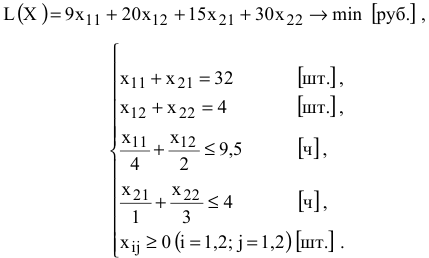
Возможно эта страница вам будет полезна:
| Экономико-математические методы задачи с решением и примерами |
Задача №1.03*
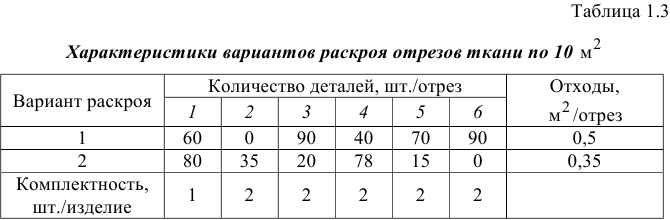
Для пошива одного изделия требуется выкроить из ткани 6 деталей. На швейной фабрике были разработаны два варианта раскроя ткани. В табл. 1.3 приведены характеристики вариантов раскроя 10  ткани и комплектность, т.е. количество деталей определенного вида, которые необходимы для пошива одного изделия. Ежемесячный запас ткани для пошива изделий данного типа составляет 405
ткани и комплектность, т.е. количество деталей определенного вида, которые необходимы для пошива одного изделия. Ежемесячный запас ткани для пошива изделий данного типа составляет 405  . В ближайший месяц планируется сшить 90 изделий.
. В ближайший месяц планируется сшить 90 изделий.
Постройте математическую модель задачи, позволяющую в ближайший месяц выполнить план по пошиву с минимальным количеством отходов.
Решение:
Переменные задачи. В данной задаче искомые величины явно не указаны, но сказано, что должен быть выполнен ежемесячный план по пошиву 90 изделий. Для пошива 90 изделий в месяц требуется раскроить строго определенное количество деталей. Крой производится из отрезов ткани по 10  двумя различными способами, которые позволяют получить различное число деталей. Поскольку заранее неизвестно, сколько ткани будет раскраиваться первым способом и сколько — вторым, то в качестве искомых величин можно задать количество отрезов ткани по 10
двумя различными способами, которые позволяют получить различное число деталей. Поскольку заранее неизвестно, сколько ткани будет раскраиваться первым способом и сколько — вторым, то в качестве искомых величин можно задать количество отрезов ткани по 10 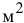 , раскроенных каждым из способов:
, раскроенных каждым из способов:
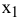 — количество отрезов ткани по 10
— количество отрезов ткани по 10 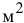 , раскроенных первым способом в течение месяца, [отрез./мес.];
, раскроенных первым способом в течение месяца, [отрез./мес.];
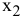 — количество отрезов ткани по 10
— количество отрезов ткани по 10 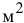 , раскроенных вторым способом в течение месяца, [отрез./мес.].
, раскроенных вторым способом в течение месяца, [отрез./мес.].
Целевая функция
Целью решения задачи является выполнение плана при минимальном количестве отходов. Поскольку количество изделий строго запланировано (90 шт./мес.), то этот параметр не описывает ЦФ, а относится к ограничению, невыполнение которого означает, что задача не решена. А критерием эффективности выполнения плана служит параметр «количество отходов», который необходимо свести к минимуму. Поскольку при раскрое одного отреза (10 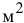 ) ткани по 1-му варианту получается 0,5
) ткани по 1-му варианту получается 0,5 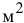 отходов, а по 2-му варианту — 0,35
отходов, а по 2-му варианту — 0,35 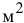 (см. табл. 1.3), то общее количество отходов при крое (ЦФ) имеет вид
(см. табл. 1.3), то общее количество отходов при крое (ЦФ) имеет вид
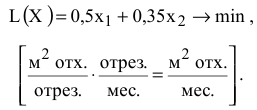
Ограничения
Количество раскроев ткани различными способами ограничивается следующими условиями:
• должен быть выполнен план по пошиву изделий, другими словами, общее количество выкроенных деталей должно быть таким, чтобы из него можно было пошить 90 изделий в месяц, а именно: деталей 1-го вида должно быть как минимум 90 и деталей остальных видов — как минимум по 180 (см. комплектность в табл. 1.3).
• расход ткани не должен превышать месячного запаса его на складе;
• количество отрезов раскроенной ткани не может быть отрицательным. Ограничения по плану пошива пальто имеют следующую содержательную форму записи

Математически эти ограничения записываются в виде
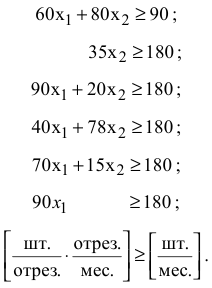
Ограничение по расходу ткани имеет следующие формы записи:
содержательную

и математическую
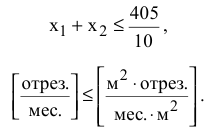
Неотрицательность количества раскроенных отрезов задается в виде
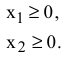
Таким образом, математическая модель задачи №1.03 имеет вид
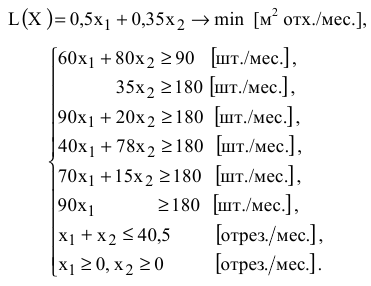
Вопрос 1.1*. При составлении математической модели задачи на следующий месяц следует учесть, что с прошлого месяца, возможно, остались выкроенные, но неиспользованные детали. Как это сделать?
Возможно эта страница вам будет полезна:
| Решение задач по ЭММ |
Графический метод решения одноиндексных задач
Графический метод довольно прост и нагляден для решения задач ЛП с двумя переменными. Он основан на геометрическом представлении допустимых решений и ЦФ задачи.
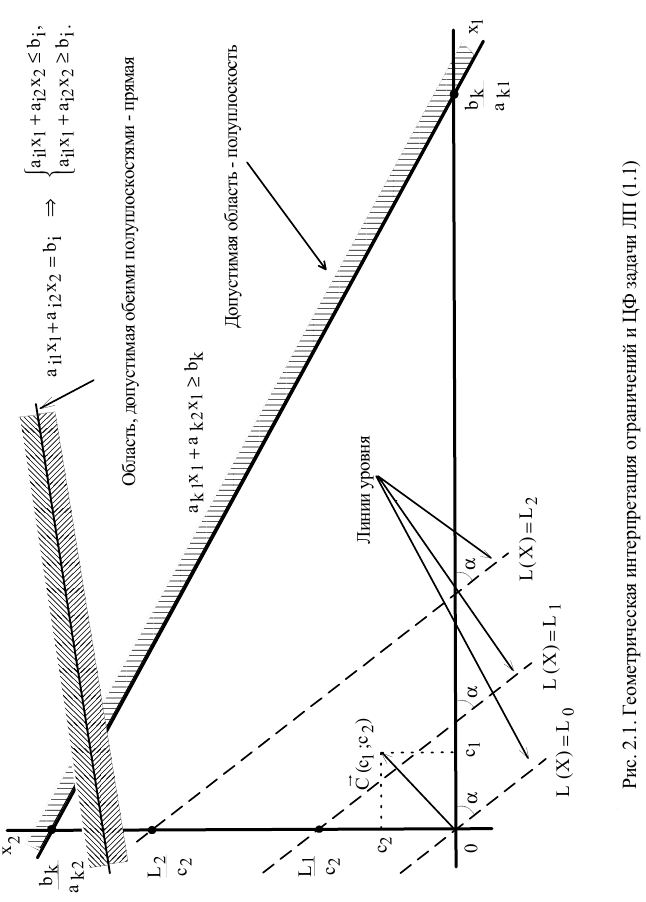
Каждое из неравенств задачи ЛП (1.1) определяет на координатной плоскости 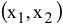 некоторую полуплоскость (рис. 2.1), а система неравенств в целом — пересечение соответствующих плоскостей. Множество точек пересечения данных полуплоскостей называется областью допустимых решений (ОДР). ОДР всегда представляет собой выпуклую фигуру, т.е. обладающую следующим свойством: если две точки
некоторую полуплоскость (рис. 2.1), а система неравенств в целом — пересечение соответствующих плоскостей. Множество точек пересечения данных полуплоскостей называется областью допустимых решений (ОДР). ОДР всегда представляет собой выпуклую фигуру, т.е. обладающую следующим свойством: если две точки 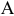 и
и 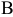 принадлежат этой фигуре, то и весь отрезок
принадлежат этой фигуре, то и весь отрезок 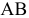 принадлежит ей. ОДР графически может быть представлена выпуклым многоугольником, неограниченной выпуклой многоугольной областью, отрезком, лучем, одной точкой. В случае несовместности системы ограничений задачи (1.1) ОДР является пустым множеством.
принадлежит ей. ОДР графически может быть представлена выпуклым многоугольником, неограниченной выпуклой многоугольной областью, отрезком, лучем, одной точкой. В случае несовместности системы ограничений задачи (1.1) ОДР является пустым множеством.
Примечание № 2.1. Все вышесказанное относится и к случаю, когда система ограничений (1.1) включает равенства, поскольку любое равенство
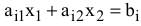
можно представить в виде системы двух неравенств (см. рис. 2.1)
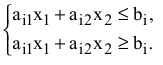
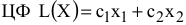 при фиксированном значении
при фиксированном значении 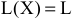 определяет на плоскости прямую линию
определяет на плоскости прямую линию 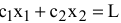 . Изменяя значения
. Изменяя значения 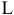 , мы получим семейство параллельных прямых, называемых линиями уровня.
, мы получим семейство параллельных прямых, называемых линиями уровня.
Это связано с тем, что изменение значения 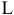 повлечет изменение лишь длины отрезка, отсекаемого линией уровня на оси
повлечет изменение лишь длины отрезка, отсекаемого линией уровня на оси 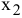 (начальная ордината), а угловой коэффициент прямой
(начальная ордината), а угловой коэффициент прямой 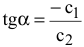 останется постоянным (см. рис. 2.1).
останется постоянным (см. рис. 2.1).
Поэтому для решения будет достаточно построить одну из линий уровня, произвольно выбрав значение 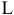 .
.
Вектор 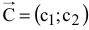 с координатами из коэффициентов ЦФ при
с координатами из коэффициентов ЦФ при  и
и 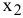 перпендикулярен к каждой из линий уровня (см. рис. 2.1). Направление вектора
перпендикулярен к каждой из линий уровня (см. рис. 2.1). Направление вектора 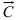 совпадает с направлением возрастания ЦФ, что является важным моментом для решения задач. Направление убывания ЦФ противоположно направлению вектора
совпадает с направлением возрастания ЦФ, что является важным моментом для решения задач. Направление убывания ЦФ противоположно направлению вектора 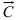 .
.
Суть графического метода заключается в следующем. По направлению (против направления) вектора 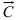 в ОДР производится поиск оптимальной точки
в ОДР производится поиск оптимальной точки 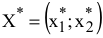 . Оптимальной считается точка, через которую проходит линия уровня
. Оптимальной считается точка, через которую проходит линия уровня 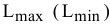 , соответствующая наибольшему (наименьшему) значению функции
, соответствующая наибольшему (наименьшему) значению функции 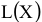 . Оптимальное решение всегда находится на границе ОДР, например, в последней вершине многоугольника ОДР, через которую пройдет целевая прямая, или на всей его стороне.
. Оптимальное решение всегда находится на границе ОДР, например, в последней вершине многоугольника ОДР, через которую пройдет целевая прямая, или на всей его стороне.
При поиске оптимального решения задач ЛП возможны следующие ситуации: существует единственное решение задачи; существует бесконечное множество решений (альтернативный оптиум); ЦФ не ограничена; область допустимых решений — единственная точка; задача не имеет решений.
Возможно эта страница вам будет полезна:
| Помощь по экономико математическим методам |
Методика решения задач графическим методом
I. В ограничениях задачи (1.1) замените знаки неравенств на знаки точных равенств и постройте соответствующие прямые.
II. Найдите и заштрихуйте полуплоскости, разрешенные каждым из ограничений-неравенств задачи (1.1). Для этого подставьте в конкретное неравенство координаты какой-либо точки [например, (0;0)], и проверьте истинность полученного неравенства.
Если неравенство истинное, то надо заштриховать полуплоскость, содержащую данную точку;
иначе (неравенство ложное) надо заштриховать полуплоскость, не содержащую данную точку.
Поскольку  и
и 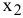 должны быть неотрицательными, то их допустимые значения всегда будут находиться выше оси
должны быть неотрицательными, то их допустимые значения всегда будут находиться выше оси  и правее оси
и правее оси 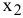 , т.е. в 1-м квадранте.
, т.е. в 1-м квадранте.
Ограничения-равенства разрешают только те точки, которые лежат на соответствующей прямой, поэтому выделите на графике такие прямые.
III. Определите ОДР как часть плоскости, принадлежащую одновременно всем разрешенным областям, и выделите ее. При отсутствии ОДР задача не имеет решении, о чем сделайте соответствующий вывод.
IV. Если ОДР — не пустое множество, то постройте целевую прямую, т.е. любую из линий уровня 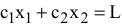 , где
, где 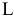 — произвольное число, например, кратное
— произвольное число, например, кратное 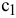 и
и 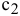 , т.е. удобное для проведения расчетов. Способ построения аналогичен построению прямых ограничений.
, т.е. удобное для проведения расчетов. Способ построения аналогичен построению прямых ограничений.
V. Постройте вектор 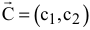 , который начинается в точке (0;0), заканчивается в точке
, который начинается в точке (0;0), заканчивается в точке 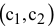 . Если целевая прямая и вектор
. Если целевая прямая и вектор 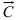 построены верно, то они будут перпендикулярны.
построены верно, то они будут перпендикулярны.
VI. При поиске max ЦФ передвигайте целевую прямую в направлении вектора 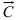 , при поиске min ЦФ — против направления вектора
, при поиске min ЦФ — против направления вектора 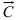 . Последняя по ходу движения вершина ОДР будет точкой max или min ЦФ. Если такой точки (точек) не существует, то сделайте вывод о неограниченности ЦФ на множестве планов сверху (при поиске max) или снизу (при поиске min).
. Последняя по ходу движения вершина ОДР будет точкой max или min ЦФ. Если такой точки (точек) не существует, то сделайте вывод о неограниченности ЦФ на множестве планов сверху (при поиске max) или снизу (при поиске min).
VII. Определите координаты точки max (min) ЦФ 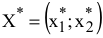 и вычислите значение ЦФ
и вычислите значение ЦФ 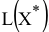 . Для вычисления координат оптимальной точки
. Для вычисления координат оптимальной точки 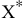 решите систему уравнений прямых, на пересечении которых находится
решите систему уравнений прямых, на пересечении которых находится 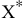 .
.
Задача №2.01
Найдем оптимальное решение задачи № 1.01 о красках, математическая модель которой имеет вид
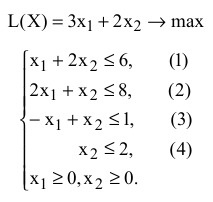
Построим прямые ограничений, для чего вычислим координаты точек пересечения этих прямых с осями координат (рис. 2.2).
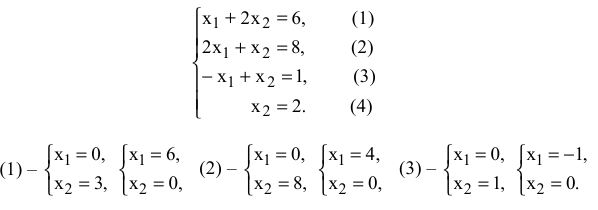
Прямая (4) проходит через точку 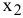 = 2 параллельно оси
= 2 параллельно оси  .
.
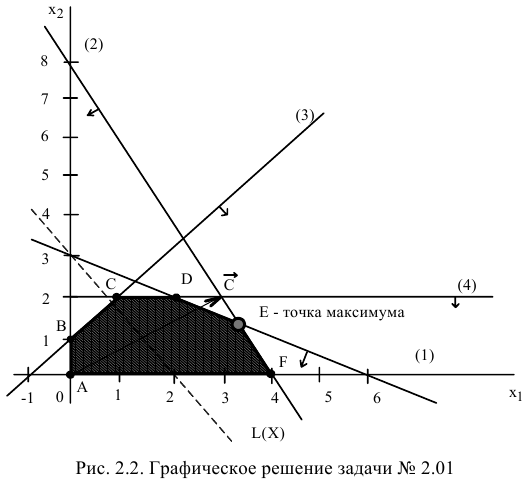
Определим ОДР. Например, подставим точку (0;0) в исходное ограничение (3), получим 0 < 1, что является истинным неравенством, поэтому стрелкой (или штрихованием) обозначим полуплоскость, содержащую точку (0;0), т.е. расположенную правее и ниже прямой (3). Аналогично определим допустимые полуплоскости для остальных ограничений и укажем их стрелками у соответствующих прямых ограничений (см. рис. 2.2). Общей областью, разрешенной всеми ограничениями, т.е. ОДР является многоугольник 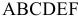 .
.
Целевую прямую можно построить по уравнению
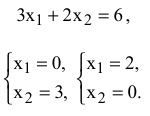
Строим вектор 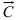 из точки (0;0) в точку (3;2). Точка
из точки (0;0) в точку (3;2). Точка 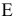 — это последняя вершина многоугольника допустимых решений
— это последняя вершина многоугольника допустимых решений 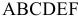 , через которую проходит целевая прямая, двигаясь по направлению вектора
, через которую проходит целевая прямая, двигаясь по направлению вектора 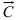 . Поэтому
. Поэтому 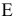 -это точка максимума ЦФ. Определим координаты точки
-это точка максимума ЦФ. Определим координаты точки 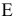 из системы уравнений прямых ограничений (1) и (2)
из системы уравнений прямых ограничений (1) и (2)
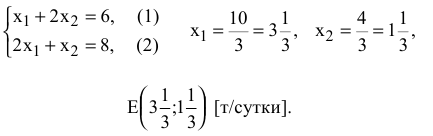
Максимальное значение ЦФ равно
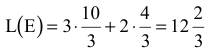
[тыс. руб./сутки]. Таким образом, наилучшим режимом работы фирмы является ежесуточное производство краски 1-го вида в объеме 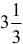 т и краски 2-го вида в объеме
т и краски 2-го вида в объеме 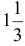 — т. Доход от продажи красок составит
— т. Доход от продажи красок составит 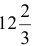 тыс. руб. в сутки.
тыс. руб. в сутки.
Задача № 2.02
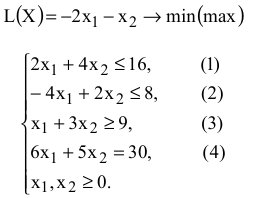
Построим ограничения (рис. 2.3).
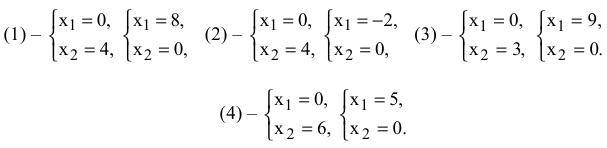
Целевую прямую построим по уравнению
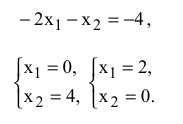
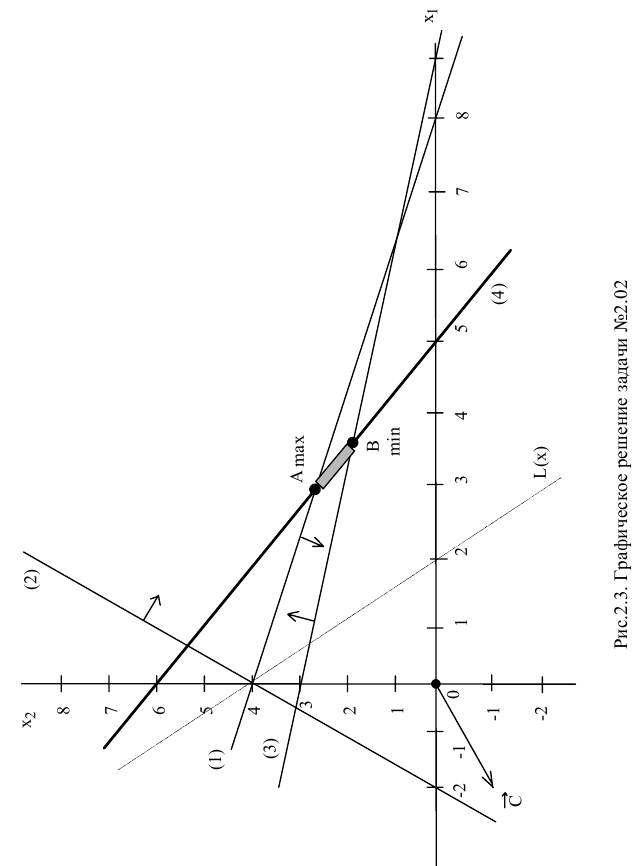
Определим ОДР. Ограничение-равенство (4) допускает только точки, лежащие на прямой (4). Подставим точку (0;0) в ограничение (3), получим 0 >9, что является ложным неравенством, поэтому стрелкой (или штрихованием) обозначим полуплоскость, не содержащую точку (0;0), т.е. расположенную выше прямой (3). Аналогично определим и укажем допустимые полуплоскости для остальных ограничений (см. рис. 2.3). Анализ полуплоскостей, допустимых остальными ограничениями-неравенствами, позволяет определить, что ОДР — это отрезок 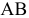 .
.
Строим вектор 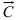 из точки (0;0) в точку (-2;-1). Для поиска минимума ЦФ двигаем целевую прямую против направления вектора
из точки (0;0) в точку (-2;-1). Для поиска минимума ЦФ двигаем целевую прямую против направления вектора 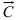 . Точка
. Точка 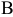 — это последняя точка отрезка
— это последняя точка отрезка 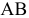 , через которую проходит целевая прямая, т.е.
, через которую проходит целевая прямая, т.е. 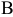 -точка минимума ЦФ.
-точка минимума ЦФ.
Определим координаты точки 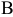 из системы уравнений прямых ограничений (3) и (4)
из системы уравнений прямых ограничений (3) и (4)

Минимальное значение ЦФ равно
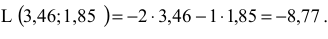
При поиске точки максимума ЦФ будем двигать целевую прямую по направлению вектора 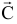 . Последней точкой отрезка
. Последней точкой отрезка 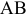 , а значит, и точкой максимума будет
, а значит, и точкой максимума будет 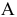 . Определим координаты точки
. Определим координаты точки 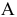 из системы уравнений прямых ограничений (1) и (4)
из системы уравнений прямых ограничений (1) и (4)

Максимальное значение ЦФ равно
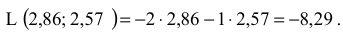
Таким образом, 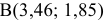 — точка минимума,
— точка минимума, 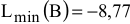 ;
; 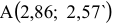 — точка максимума,
— точка максимума, 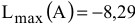 .
.
Задача № 2.03
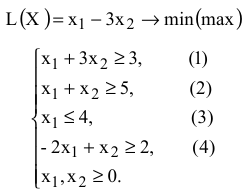
Построим ограничения (рис. 2.4)
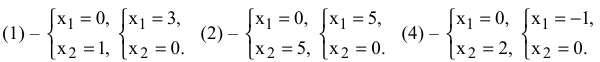
Прямая (3) — проходит через точку 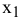 = 4 параллельно оси
= 4 параллельно оси 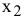 . Целевую прямую построим по уравнению
. Целевую прямую построим по уравнению
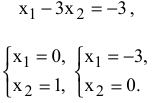
Определим ОДР. Подставим точку (0;0) в ограничение (2), получим 0 > 5, что является ложным неравенством, поэтому стрелкой (или штрихованием) обозначим полуплоскость, не содержащую точку (0;0), т.е. расположенную правее и выше прямой (2).
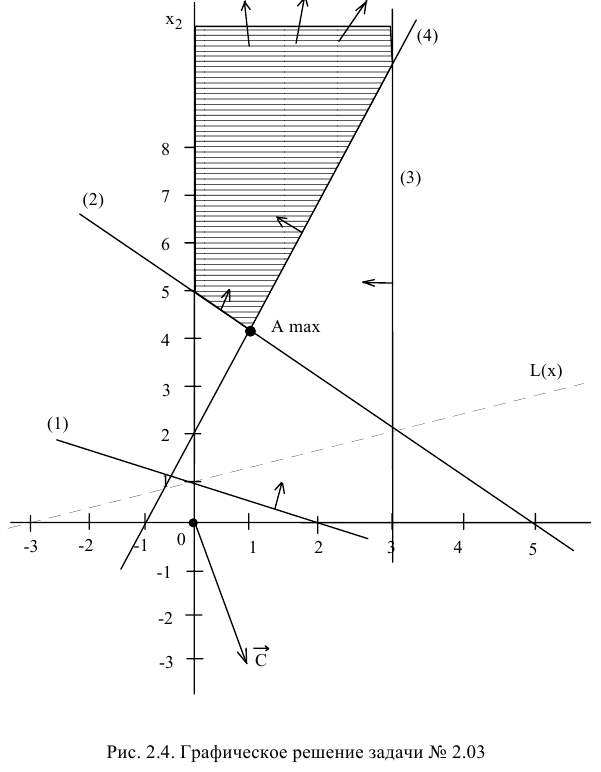
Аналогично определим и укажем допустимые полуплоскости для остальных ограничений (см. рис.2.4). Анализ допустимых полуплоскостей позволяет определить, что ОДР — это незамкнутая область, ограниченная прямыми (2), (3), (4) и осью 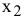 .
.
Строим вектор 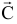 из точки (0;0) в точку (1;-3). Для поиска минимума ЦФ двигаем целевую прямую против направления вектора
из точки (0;0) в точку (1;-3). Для поиска минимума ЦФ двигаем целевую прямую против направления вектора 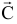 . Поскольку в этом направлении ОДР не ограничена, то невозможно в этом направлении найти последнюю точку ОДР. Отсюда следует, что ЦФ не ограничена на множестве планов снизу (поскольку идет поиск минимума).
. Поскольку в этом направлении ОДР не ограничена, то невозможно в этом направлении найти последнюю точку ОДР. Отсюда следует, что ЦФ не ограничена на множестве планов снизу (поскольку идет поиск минимума).
При поиске максимума ЦФ будем двигать целевую прямую по направлению вектора 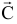 до пересечения с вершиной
до пересечения с вершиной 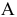 — последней точкой ОДР в этом направлении. Определим координаты точки
— последней точкой ОДР в этом направлении. Определим координаты точки 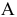 из системы уравнений прямых ограничений (2) и (4)
из системы уравнений прямых ограничений (2) и (4)

Максимальное значение ЦФ равно
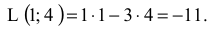
Таким образом, в данной задаче ЦФ не ограничена на множестве планов снизу а 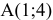 является точкой максимума ЦФ,
является точкой максимума ЦФ, 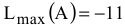 .
.
Возможно эта страница вам будет полезна:
| Курсовая работа по экономико математическим методам |
Анализ чувствительности оптимального решения одноиндексных задач
Неизбежное колебание значений таких экономических параметров, как цены на продукцию и сырье, запасы сырья, спрос на рынке и т.д. может привести к неоптимальности или непригодности прежнего режима работы. Для учета подобных ситуаций проводится анализ чувствительности, т.е. анализ того, как возможные изменения параметров исходной модели повлияют на полученное ранее оптимальное решение задачи ЛП.
Для решения задач анализа чувствительности ограничения линейной модели классифицируются следующим образом. Связывающие ограничения проходят через оптимальную точку. Несвязывающие ограничения не проходят через оптимальную точку. Аналогично ресурс, представляемый связывающим ограничением, называют дефицитным, а ресурс, представляемый несвязывающим ограничением — недефицитным. Ограничение называют избыточным в том случае, если его исключение не влияет на ОДР и, следовательно, на оптимальное решение. Выделяют следующие три задачи анализа на чувствительность.
Анализ сокращения или увеличения ресурсов:
• на сколько можно увеличить (ограничения типа 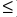 ) запас дефицитного ресурса для улучшения оптимального значения ЦФ?
) запас дефицитного ресурса для улучшения оптимального значения ЦФ?
• на сколько можно уменьшить (ограничения типа 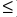 ) запас недефицитного ресурса при сохранении оптимального значения ЦФ?
) запас недефицитного ресурса при сохранении оптимального значения ЦФ?
- Увеличение (ограничения типа
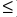 ) запаса какого из ресурсов наиболее выгодно?
) запаса какого из ресурсов наиболее выгодно? - Анализ изменения коэффициентов ЦФ: каков диапазон изменения коэффициентов ЦФ, при котором не меняется оптимальное решение?
Методика графического анализа чувствительности оптимального решения
Первая задача анализа на чувствительность (анализ на чувствительность к правой части ограничений)
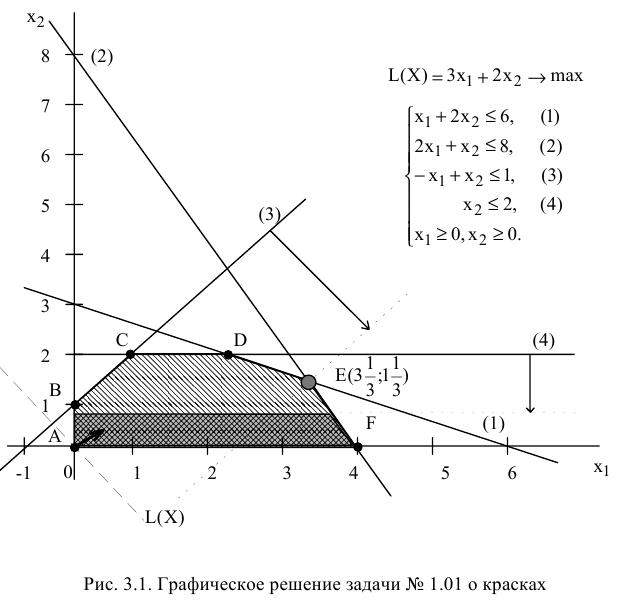
Проанализируем чувствительность оптимального решения задачи № 1.01 о производстве красок. ОДР задачи № 1.01 (рис. 3.1)- многоугольник 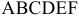 . В оптимальной точке
. В оптимальной точке 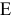 пересекаются прямые (1) и (2). Поэтому ограничения (1) и (2) являются связывающими, а соответствующие им ресурсы (ингредиенты
пересекаются прямые (1) и (2). Поэтому ограничения (1) и (2) являются связывающими, а соответствующие им ресурсы (ингредиенты 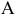 и
и 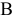 ) — дефицитными.
) — дефицитными.
Рассмотрим экономический смысл этих понятий. Точка максимума ЦФ 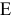 соответствует суточному производству
соответствует суточному производству 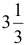 т краски 1-го вида и
т краски 1-го вида и 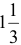 т краски 2-го вида. В производстве красок используются ингредиенты
т краски 2-го вида. В производстве красок используются ингредиенты 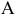 и
и 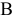 . Суточный запас на складе ингредиентов
. Суточный запас на складе ингредиентов 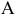 и
и 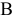 — это правые части связывающих ограничений (1) и (2) (6 и 8 т ингр./сутки). Согласно этим ограничениям, на производство в точке
— это правые части связывающих ограничений (1) и (2) (6 и 8 т ингр./сутки). Согласно этим ограничениям, на производство в точке 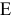 расходуется
расходуется
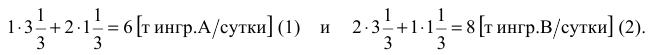
Таким образом, понятие «связывающие ограничения» (1) и (2) означает, что при производстве красок в точке 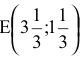 запасы ингредиентов
запасы ингредиентов 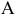 и
и 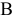 расходуются полностью и по этой причине невозможно дальнейшее наращивание производства.
расходуются полностью и по этой причине невозможно дальнейшее наращивание производства.
В этом заключается экономический смысл понятия дефицитности ресурсов, т.е. если фирма сможет увеличить суточные запасы ингредиентов, то это позволит увеличить выпуск красок.
В связи с этим возникает вопрос: до какого уровня целесообразно увеличить запасы ингредиентов и на сколько при этом увеличится оптимальное производство красок?
Правило № 3.1
Чтобы графически определить максимальное увеличение запаса дефицитного ресурса, вызывающее улучшение оптимального решения, необходимо передвигать соответствующую прямую в направлении улучшения ЦФ до тех пор, пока это ограничение не станет избыточным.
При прохождении прямой (1) через точку 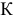 (рис. 3.2) многоугольник
(рис. 3.2) многоугольник 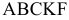 становится ОДР, а ограничение (1) — избыточным. Действительно, если удалить прямую (1), проходящую через точку
становится ОДР, а ограничение (1) — избыточным. Действительно, если удалить прямую (1), проходящую через точку 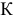 , то ОДР
, то ОДР 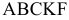 не изменится. Точка
не изменится. Точка 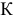 становится оптимальной, в этой точке ограничения (2) и (4) становятся связывающими.
становится оптимальной, в этой точке ограничения (2) и (4) становятся связывающими.
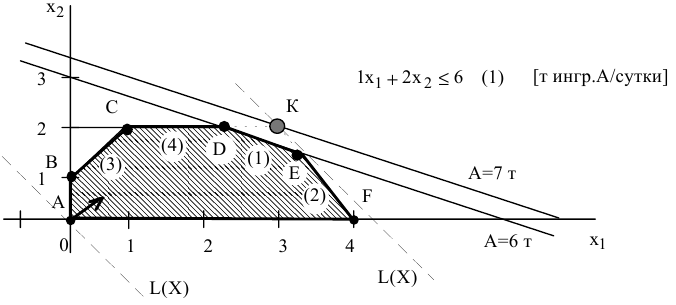
Правило № 3.2
Чтобы численно определить максимальную величину запаса дефицитного ресурса, вызывающую улучшение оптимального решения, необходимо: 1) определить координаты точки 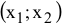 , в которой соответствующее ограничение становится избыточным;
, в которой соответствующее ограничение становится избыточным;
2) подставить координаты 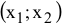 в левую часть соответствующего ограничения.
в левую часть соответствующего ограничения.
Координаты точки 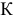 (3;2) находятся путем решения системы уравнений прямых (2) и (4). Т.е. в этой точке фирма будет производить Зт краски 1-го вида и 2т краски 2-го вида. Подставим
(3;2) находятся путем решения системы уравнений прямых (2) и (4). Т.е. в этой точке фирма будет производить Зт краски 1-го вида и 2т краски 2-го вида. Подставим 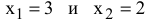 в левую часть ограничения (1) и получим максимально допустимый запас ингредиента
в левую часть ограничения (1) и получим максимально допустимый запас ингредиента 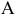
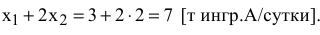
Дальнейшее увеличение запаса ингредиента 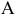 нецелесообразно, потому что это не изменит ОДР и не приведет к другому оптимальному решению (см. рис. 3.2). Доход от продажи красок в объеме, соответствующем точке
нецелесообразно, потому что это не изменит ОДР и не приведет к другому оптимальному решению (см. рис. 3.2). Доход от продажи красок в объеме, соответствующем точке 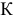 , можно рассчитать, подставив ее координаты (3;2) в выражение ЦФ
, можно рассчитать, подставив ее координаты (3;2) в выражение ЦФ
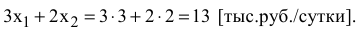
Рассмотрим вопрос о целесообразности увеличения запаса ингредиента 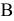 . Согласно правилу № 3.1, соответствующее ограничение (2) становится избыточным в точке
. Согласно правилу № 3.1, соответствующее ограничение (2) становится избыточным в точке 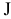 , в которой пересекаются прямая (1) и ось переменной
, в которой пересекаются прямая (1) и ось переменной 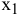 (рис. 3.3). Многоугольник
(рис. 3.3). Многоугольник 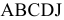 становится ОДР, а точка
становится ОДР, а точка 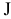 (6;0) -оптимальным решением.
(6;0) -оптимальным решением.
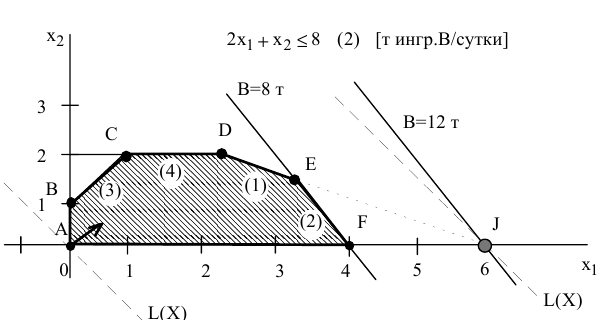
В точке 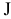 выгодно производить только краску 1-го вида (6 т в сутки). Доход от продажи при этом составит
выгодно производить только краску 1-го вида (6 т в сутки). Доход от продажи при этом составит
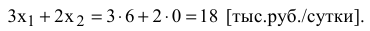
Чтобы обеспечить такой режим работы, согласно правилу № 3.2, запас ингредиента В надо увеличить до величины
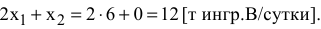
Ограничения (3) и (4) являются не связывающими, т.к. не проходят через оптимальную точку 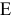 (см. рис. 3.1). Соответствующие им ресурсы (спрос на краски) являются недефицитными. С экономической точки зрения это означает, что в данный момент уровень спроса на краски непосредственно не определяет объемы производства. Поэтому некоторое его колебание может никак не повлиять на оптимальный режим производства в точке
(см. рис. 3.1). Соответствующие им ресурсы (спрос на краски) являются недефицитными. С экономической точки зрения это означает, что в данный момент уровень спроса на краски непосредственно не определяет объемы производства. Поэтому некоторое его колебание может никак не повлиять на оптимальный режим производства в точке 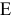 .
.
Например, увеличение (уменьшение) спроса на краску 2-го вида будет соответствовать перемещению прямой ограничения 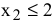 (4) вверх (вниз). Перемещение прямой (4) вверх никак не может изменить точку
(4) вверх (вниз). Перемещение прямой (4) вверх никак не может изменить точку 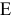 максимума ЦФ. Перемещение же прямой (4) вниз не влияет на существующее оптимальное решение только до пересечения с точкой
максимума ЦФ. Перемещение же прямой (4) вниз не влияет на существующее оптимальное решение только до пересечения с точкой 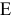 (см. правило № 3.3). Из рис. 3.1 видно, что дальнейшее перемещение (4) приведет к тому, что точка
(см. правило № 3.3). Из рис. 3.1 видно, что дальнейшее перемещение (4) приведет к тому, что точка 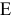 будет за пределами новой ОДР, выделенной более темным цветом. Кроме того, любое оптимальное решение для этой новой ОДР будет хуже точки
будет за пределами новой ОДР, выделенной более темным цветом. Кроме того, любое оптимальное решение для этой новой ОДР будет хуже точки 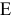 .
.
Правило № 3.3
Чтобы определить максимальное уменьшение запаса недефицитного ресурса, не меняющее оптимальное решение,
необходимо передвигать соответствующую прямую до пересечения с оптимальной точкой.
Правило № 3.4
Чтобы численно определить минимальную величину запаса недефицитного ресурса, не меняющую оптимальное решение,
необходимо подставить координаты оптимальной точки в левую часть соответствующего ограничения.
Чтобы выяснить, до каких пределов падение спроса на краску 2-го вида не повлияет на производство в точке 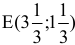 используем правило № 3.4.
используем правило № 3.4.
Подставляем в левую часть ограничения (4) координаты точки 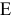 , получаем
, получаем
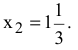
Делаем вывод: предельный уровень, до которого может упасть спрос на краску 2-го вида и при котором не изменится оптимальность полученного ране решения, равен 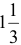 т краски в сутки.
т краски в сутки.
Экономический смысл ограничения (3)
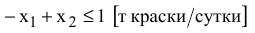
в том, что объем продаж краски 2-го вида может превысить объем продаж краски 1-го вида максимум на 1 т. Дальнейшее увеличение продаж краски 2-го вида по сравнению с краской 1-го вида графически отобразится перемещением прямой (3) влево и вверх, но никак не повлияет на оптимальность точки 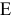 . Но если разность спросов на краску 2-го и 1-го видов будет уменьшаться, то прямая (3) будет перемещаться ниже и правее. Последним положением прямой (3), при котором точка
. Но если разность спросов на краску 2-го и 1-го видов будет уменьшаться, то прямая (3) будет перемещаться ниже и правее. Последним положением прямой (3), при котором точка 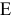 остается оптимальной, является пересечение с точкой
остается оптимальной, является пересечение с точкой 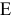 (см. рис. 3.1). Согласно правилу № 3.4, подставим координаты точки
(см. рис. 3.1). Согласно правилу № 3.4, подставим координаты точки
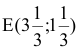
в левую часть ограничения (3)
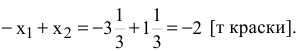
Получаем, что разность спросов на краску 2-го и 1 -го вида в точке стала отрицательной. То есть, прохождение прямой (3) через точку 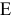 означает, что краску 2-го вида будут покупать в меньшем объеме, чем краску 1-го вида
означает, что краску 2-го вида будут покупать в меньшем объеме, чем краску 1-го вида
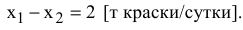
Делаем вывод: максимальное превышение спроса на краску 1-го вида над спросом на краску 2-го вида, при котором оптимальное решение в точке 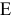 не изменится, составляет 2 т краски в сутки.
не изменится, составляет 2 т краски в сутки.
Результаты решения первой задачи анализа оптимального решения на чувствительность представлены в табл. 3.1.

Вторая задача анализа на чувствительность
Анализ табл. 3.1 показывает, что к улучшению оптимального решения, т.е. к увеличению суточного дохода приводит увеличение дефицитных ресурсов. Для определения выгодности увеличения этих ресурсов используют понятие ценности дополнительной единицы 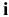 -го ресурса
-го ресурса 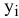
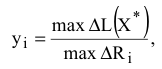
где 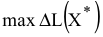 — максимальное приращение оптимального значения ЦФ;
— максимальное приращение оптимального значения ЦФ; 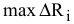 — максимально допустимый прирост объема
— максимально допустимый прирост объема 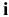 -го ресурса.
-го ресурса.
Например, из табл. 3.1 следует, что увеличение суточного запаса ингредиента 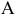 [ограничение (1)] на 1т позволит получить дополнительный доход, равный
[ограничение (1)] на 1т позволит получить дополнительный доход, равный 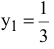 тыс. руб. / сутки, в то время как увеличение запаса
тыс. руб. / сутки, в то время как увеличение запаса 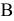 [ограничение (2)] на 1т принесет
[ограничение (2)] на 1т принесет 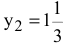 тыс. руб. / сутки. Недефицитные ресурсы имеют нулевые ценности, поскольку изменение этих ресурсов не приводит к увеличению дохода.
тыс. руб. / сутки. Недефицитные ресурсы имеют нулевые ценности, поскольку изменение этих ресурсов не приводит к увеличению дохода.
Вывод: дополнительные вложения в первую очередь необходимо направлять на увеличение ресурса 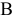 , а лишь потом на ресурс
, а лишь потом на ресурс 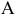 . Изменять недефицитные ресурсы нет необходимости.
. Изменять недефицитные ресурсы нет необходимости.
Третья задача анализа на чувствительность
Графический анализ допустимого диапазона изменения цен
Изменение цен на продукцию, т.е. изменение коэффициентов ЦФ, представляется на графике вращением целевой прямой вокруг оптимальной точки. Так, при увеличении коэффициента ЦФ 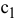 или уменьшении
или уменьшении 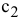 целевая прямая вращается по часовой стрелке. При уменьшении
целевая прямая вращается по часовой стрелке. При уменьшении 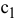 или же увеличении
или же увеличении 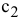 целевая прямая вращается против часовой стрелки (рис. 3.4).
целевая прямая вращается против часовой стрелки (рис. 3.4).
При таких поворотах точка 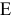 будет оставаться оптимальной до тех пор, пока наклон целевой прямой не выйдет за пределы, определяемые наклонами прямых ограничений (1) и (2). Так, например, если наклон целевой прямой совпадет с наклоном прямой (1), то оптимальным решением будут точки отрезка
будет оставаться оптимальной до тех пор, пока наклон целевой прямой не выйдет за пределы, определяемые наклонами прямых ограничений (1) и (2). Так, например, если наклон целевой прямой совпадет с наклоном прямой (1), то оптимальным решением будут точки отрезка 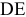 .
.
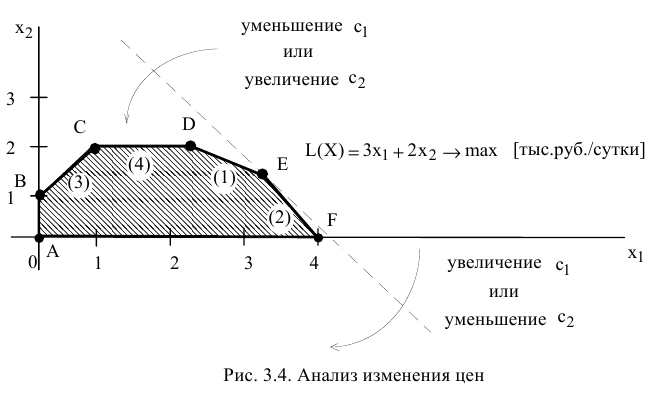
При совпадении с прямой (2) оптимальным решением будут точки отрезка 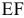 . Если целевая прямая выйдет за пределы наклона (1) или (2), то оптимальной точкой станет соответственно
. Если целевая прямая выйдет за пределы наклона (1) или (2), то оптимальной точкой станет соответственно 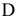 или
или 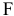 .
.
Допустим, что цена на краску 2-го вида не меняется, т.е. зафиксируем значение целевого коэффициента 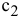 . Проанализируем графически результаты изменения значения целевого коэффициент
. Проанализируем графически результаты изменения значения целевого коэффициент 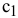 т.е. цены на краску 1-го вида. Оптимальное решение в точке
т.е. цены на краску 1-го вида. Оптимальное решение в точке 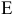 не будет меняться при увеличении
не будет меняться при увеличении 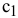 до тех пор, пока целевая прямая не совпадет с прямой (2). Аналогично, оптимальное решение в точке
до тех пор, пока целевая прямая не совпадет с прямой (2). Аналогично, оптимальное решение в точке 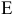 не будет меняться при уменьшении
не будет меняться при уменьшении 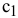 до тех пор, пока целевая прямая не совпадет с прямой (1).
до тех пор, пока целевая прямая не совпадет с прямой (1).
Аналитический поиск допустимого диапазона изменения цен
Совпадение в процессе вращения целевой прямой с прямой ограничения означает, что углы их наклона относительно горизонтальной оси сравнялись, а значит, стали равны тангенсы углов наклона этих прямых.
Чтобы определить границы допустимого диапазона изменения коэффициента ЦФ, например 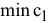 и
и 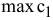 ,
,
необходимо приравнять тангенс угла наклона целевой прямой 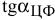 поочередно к тангенсам углов наклона прямых связывающих ограничений, например
поочередно к тангенсам углов наклона прямых связывающих ограничений, например 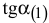 и
и 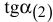 (рис. 3.5 и 3.6).
(рис. 3.5 и 3.6).
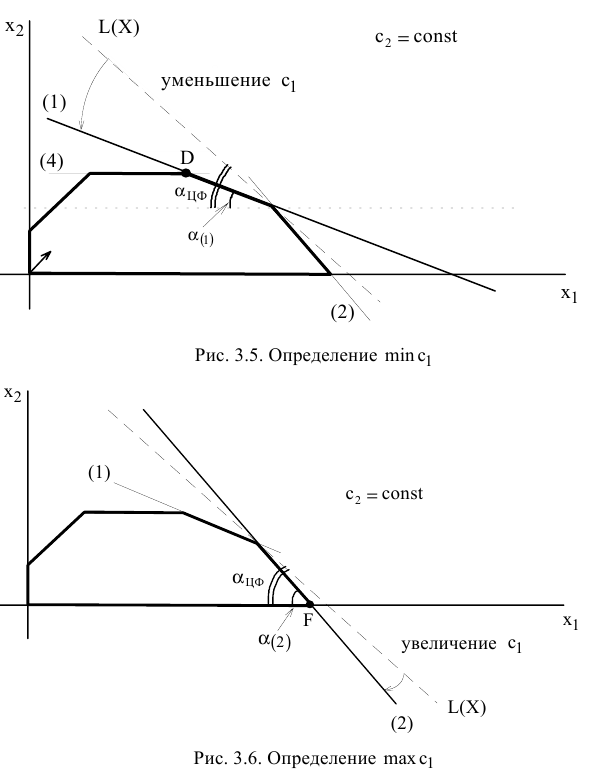
Определим насколько максимально может снизиться цена на краску 1-го вида, не изменяя оптимальную точку 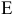 . Для этого применим правило № 3.5 и формулу расчета тангенса угла наклона прямой (рис. 3.7).
. Для этого применим правило № 3.5 и формулу расчета тангенса угла наклона прямой (рис. 3.7).
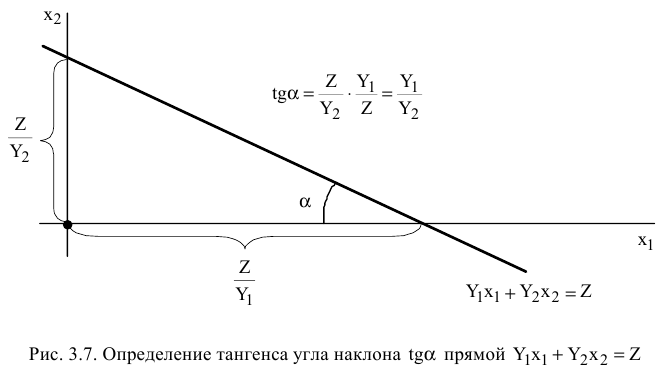
Определим тангенсы углов наклона:
1) целевой прямой 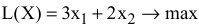 , учитывая, что
, учитывая, что 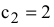 фиксировано
фиксировано
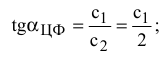
2) связывающего ограничения
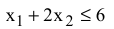
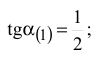
3) связывающего ограничения
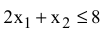
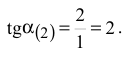
Для нахождения 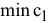 целевая прямая должна совпасть с прямой (1) (см. рис. 3.5):
целевая прямая должна совпасть с прямой (1) (см. рис. 3.5):
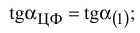
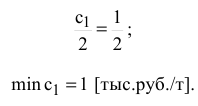
Для нахождения 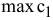 целевая прямая должна совпасть с прямой (2) (см. рис. 3.6):
целевая прямая должна совпасть с прямой (2) (см. рис. 3.6):
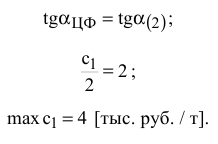
Таким образом, если цены на краску первого вида будут колебаться в пределах 1 < 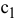 < 4 тыс. руб. / т, то оптимальное решение задачи не изменится.
< 4 тыс. руб. / т, то оптимальное решение задачи не изменится.
Из приведенных выше расчетов и графической их иллюстрации следует, что если цена на краску первого вида станет меньше 1 тыс. руб. / т (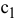 <1), то наиболее выгодным будет производство красок в точке
<1), то наиболее выгодным будет производство красок в точке 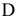 (см. рис. 3.5). При этом общее потребление ингредиента
(см. рис. 3.5). При этом общее потребление ингредиента 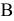 снизится, что приведет к его недефицитности [ресурс (2)], а дефицитными будут ресурсы (1) и (4).
снизится, что приведет к его недефицитности [ресурс (2)], а дефицитными будут ресурсы (1) и (4).
Возможно эта страница вам будет полезна:
| Контрольная по экономико математическим методам |
Двухиндексные задачи линейного программирования. Построение моделей транспортной задачи
Задача о размещении (транспортная задача) — это РЗ, в которой работы и ресурсы измеряются в одних и тех же единицах. В таких задачах ресурсы могут быть разделены между работами, и отдельные работы могут быть выполнены с помощью различных комбинаций ресурсов. Примером типичной транспортной задачи (ТЗ) является распределение (транспортировка) продукции, находящейся на складах, по предприятиям-потребителям.
Стандартная ТЗ определяется как задача разработки наиболее экономичного плана перевозки продукции одного вида из нескольких пунктов отправления в пункты назначения. При этом величина транспортных расходов прямо пропорциональна объему перевозимой продукции и задается с помощью тарифов на перевозку единицы продукции.
Исходные параметры модели ТЗ
1) 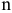 — количество пунктов отправления,
— количество пунктов отправления, 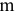 — количество пунктов назначения.
— количество пунктов назначения.
2) 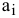 — запас продукции в пункте отправления
— запас продукции в пункте отправления 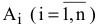 [ед. прод.].
[ед. прод.].
3) 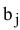 — спрос на продукцию в пункте назначения
— спрос на продукцию в пункте назначения 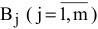 [ед. прод.].
[ед. прод.].
4) 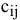 — тариф (стоимость) перевозки единицы продукции из пункта отправления
— тариф (стоимость) перевозки единицы продукции из пункта отправления 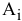 в пункт назначения
в пункт назначения 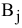 [руб. / ед. прод.].
[руб. / ед. прод.].
Искомые параметры модели ТЗ
1) 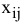 — количество продукции, перевозимой из пункта отправления
— количество продукции, перевозимой из пункта отправления 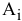 в пункт назначения
в пункт назначения 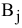 [ед. прод.].
[ед. прод.].
2) 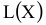 — транспортные расходы на перевозку всей продукции [руб.].
— транспортные расходы на перевозку всей продукции [руб.].
Этапы построения модели
I. Определение переменных.
И. Проверка сбалансированности задачи.
III. Построение сбалансированной транспортной матрицы.
IV. Задание ЦФ.
V. Задание ограничений.
Транспортная модель
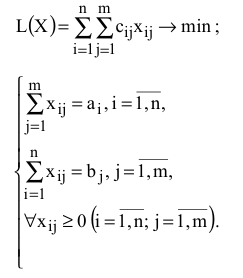
ЦФ представляет собой общие транспортные расходы на осуществление всех перевозок в целом. Первая группа ограничений указывает, что запас продукции в любом пункте отправления должен быть равен суммарному объему перевозок продукции из этого пункта. Вторая группа ограничений указывает, что суммарные перевозки продукции в некоторый пункт потребления должны полностью удовлетворить спрос на продукцию в этом пункте. Наглядной формой представления модели ТЗ является транспортная матрица (табл. 4.1).

Из модели (4.1) следует, что сумма запасов продукции во всех пунктах отправления должна равняться суммарной потребности во всех пунктах потребления, т.е.
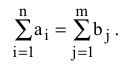
Если (4.2) выполняется, то ТЗ называется сбалансированной (закрытой), в противном случае — несбалансированной (открытой). В случае, когда суммарные запасы превышают суммарные потребности, необходим дополнительный фиктивный (реально не существующий) пункт потребления, который будет формально потреблять существующий излишек запасов, т.е.
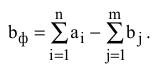
Если суммарные потребности превышают суммарные запасы, то необходим дополнительный фиктивный пункт отправления, формально восполняющий существующий недостаток продукции в пунктах отправления:
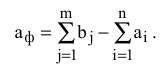
Для фиктивных перевозок вводятся фиктивные тарифы 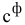 , величина которых обычно приравнивается к нулю
, величина которых обычно приравнивается к нулю 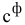 =0. Но в некоторых ситуациях величину фиктивного тарифа можно интерпретировать как штраф, которым облагается каждая единица недопоставленной продукции. В этом случае величина
=0. Но в некоторых ситуациях величину фиктивного тарифа можно интерпретировать как штраф, которым облагается каждая единица недопоставленной продукции. В этом случае величина 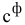 может быть любым положительным числом.
может быть любым положительным числом.
Задача о назначениях — частный случай ТЗ. В задаче о назначениях количество пунктов отправления равно количеству пунктов назначения. Объемы потребности и предложения в каждом из пунктов назначения и отправления равны 1. Примером типичной задачи о назначениях является распределение работников по различным видам работ, минимизирующее суммарное время выполнения работ.
Переменные задачи о назначениях определяются следующим образом

Возможно эта страница вам будет полезна:
| Заказать работу по экономико математическим методам |
Стандартная транспортная задача
Задача № 4.01
Заводы некоторой автомобильной фирмы расположены в городах 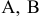 и
и 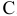 . Основные центры распределения продукции сосредоточены в городах
. Основные центры распределения продукции сосредоточены в городах 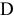 и
и  . Объемы производства указанных трех заводов равняются 1000, 1300 и 1200 автомобилей ежеквартально. Величины квартального спроса в центрах распределения составляют 2300 и 1400 автомобилей соответственно. Стоимости перевозки автомобилей по железной дороге по каждому из возможных маршрутов приведены в табл. 4.2.
. Объемы производства указанных трех заводов равняются 1000, 1300 и 1200 автомобилей ежеквартально. Величины квартального спроса в центрах распределения составляют 2300 и 1400 автомобилей соответственно. Стоимости перевозки автомобилей по железной дороге по каждому из возможных маршрутов приведены в табл. 4.2.
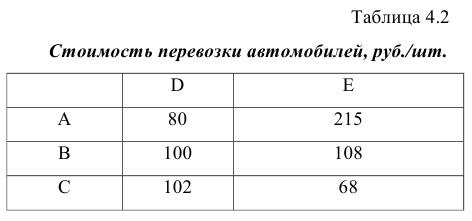
Постройте математическую модель, позволяющую определить количество автомобилей, перевозимых из каждого завода в каждый центр распределения, таким образом, чтобы общие транспортные расходы были минимальны.
Решение:
Определение переменных
Обозначим количество автомобилей, перевозимых из  -го завода в
-го завода в  -й пункт потребления через
-й пункт потребления через 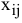 .
.
Проверка сбалансированност и зада чи
Проверим равенство суммарного производства автомобилей и суммарного спроса
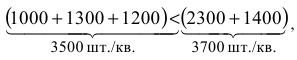
откуда следует вывод — задача несбалансирована, поскольку спрос на автомобили превышает объем их производства. Для установления баланса введем дополнительный фиктивный завод с ежеквартальным объемом производства 200 шт. (3700-3500 = 200). Фиктивные тарифы 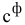 приравняем к нулю (т.к. перевозки в действительности производиться не будут).
приравняем к нулю (т.к. перевозки в действительности производиться не будут).
Построение транспортной матрицы
Согласно результатам проверки сбалансированности задачи № 4.01 в транспортной матрице должно быть четыре строки, соответствующих заводам и два столбца, соответствующих центрам распределения (см. табл. 4.3). Тариф перевозки обычно вписывают в правом нижнем углу клетки матрицы для удобства дальнейшего нахождения опорных планов задачи.
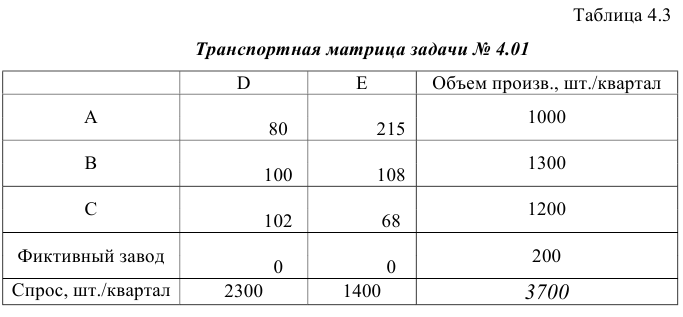
Задание ЦФ
Суммарные затраты в рублях на ежеквартальную перевозку автомобилей определяются по формуле

Модификации стандартной транспортной задачи
Недопустимые перевозки
Иногда в определенных направлениях перевозки продукции невозможны, например, по причине ремонта транспортных магистралей. Такие ситуации моделируются с помощью введения так называемых запрещающих тарифов 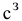 . Запрещающие тарифы должны сделать невыгодными перевозки в соответствующих направлениях. Для этого величина запрещающих тарифов должна быть больше реальных тарифов в транспортной матрице
. Запрещающие тарифы должны сделать невыгодными перевозки в соответствующих направлениях. Для этого величина запрещающих тарифов должна быть больше реальных тарифов в транспортной матрице
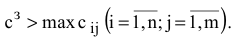
Максимизация ЦФ
Существующий алгоритм решения транспортных задач (метод потенциалов) предполагает, что ЦФ стремится к минимуму. Однако существуют ситуации, когда в рамках транспортной модели требуется максимизировать ЦФ, например, общий доход, объем продаж, прибыль, качество выполняемых работ и т.д. В этом случае в модель вместо искомой ЦФ 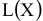 вводится ЦФ
вводится ЦФ 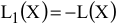 , в которой тарифы умножаются на (-1). Таким образом, максимизация
, в которой тарифы умножаются на (-1). Таким образом, максимизация 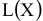 будет соответствовать минимизации
будет соответствовать минимизации 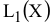 .
.
Много продуктовые модели
Если в задаче идет речь о том, что из каждого пункта отправления можно перевозить продукцию нескольких видов, то при построении модели можно использовать один из следующих вариантов:
• каждому виду продукции должна соответствовать одна транспортная матрица;
• все виды продукции представлены в одной общей матрице с использованием запрещающих тарифов в клетках, связывающих разные виды продукции.
Методы нахождения опорных планов
Опорный план является допустимым решением ТЗ и используется в качестве начального базисного решения при нахождении оптимального решения методом потенциалов. Существует три метода нахождения опорных планов: метод северо-западного угла, метод минимального элемента и метод Фогеля. «Качество» опорных планов, полученных этими методами, различается: в общем случае метод Фогеля дает наилучшее решение (зачастую оптимальное), а метод северо-западного угла — наихудшее.
Все существующие методы нахождения опорных планов отличаются только способом выбора клетки для заполнения. Само заполнение происходит одинаково независимо от используемого метода. Следует помнить, что перед нахождением опорного плана транспортная задача должна быть сбалансирована.
Метод северо-западного угла
На каждом шаге метода северо-западного угла из всех не вычеркнутых клеток выбирается самая левая и верхняя (северо-западная) клетка. Другими словами, на каждом шаге выбирается первая из оставшихся не вычеркнутых строк и первый из оставшихся не вычеркнутых столбцов.
Для того, чтобы заполнить клетку 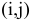 , необходимо сравнить текущий запас товара в рассматриваемой
, необходимо сравнить текущий запас товара в рассматриваемой 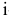 -й строке
-й строке 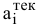 с текущей потребностью в рассматриваемом
с текущей потребностью в рассматриваемом 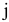 -м столбце
-м столбце 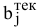 .
.
Если существующий запас позволяет перевезти всю потребность, то
• в клетку 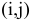 в качестве перевозки вписывается значение потребности
в качестве перевозки вписывается значение потребности 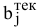 ;
;
• 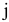 -й столбец вычеркивается, поскольку его потребность уже исчерпана;
-й столбец вычеркивается, поскольку его потребность уже исчерпана;
• от существующего запаса в 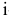 -й строке отнимается величина сделанной перевозки, прежний запас зачеркивается, а вместо него записывается остаток, т.е.
-й строке отнимается величина сделанной перевозки, прежний запас зачеркивается, а вместо него записывается остаток, т.е. 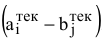 .
.
Если существующий запас не позволяет перевезти всю потребность, то
• в клетку 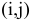 в качестве перевозки вписывается значение запаса
в качестве перевозки вписывается значение запаса 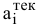 ;
;
• 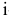 -я строка вычеркивается, поскольку ее запас уже исчерпан;
-я строка вычеркивается, поскольку ее запас уже исчерпан;
• от существующей потребности в 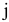 -й строке отнимается величина сделанной перевозки, прежняя потребность зачеркивается, а вместо нее записывается остаток, т.е.
-й строке отнимается величина сделанной перевозки, прежняя потребность зачеркивается, а вместо нее записывается остаток, т.е. 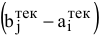
Нахождение опорного плана продолжается до тех пор, пока не будут вычеркнуты все строки и столбцы.
Метод минимального элемента
На каждом шаге метода минимального элемента из всех не вычеркнутых клеток транспортной матрицы выбирается клетка с минимальной стоимостью перевозки 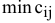 . Заполнение выбранной клетки производится по правилам, описанным выше.
. Заполнение выбранной клетки производится по правилам, описанным выше.
Метод Фогеля
На каждом шаге метода Фогеля для каждой 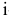 -й строки вычисляются штрафы
-й строки вычисляются штрафы 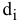 как разность между двумя наименьшими тарифами строки. Таким же образом вычисляются штрафы
как разность между двумя наименьшими тарифами строки. Таким же образом вычисляются штрафы 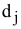 для каждого
для каждого 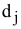 -го столбца. После чего
-го столбца. После чего
выбирается максимальный штраф из всех штрафов строк и столбцов. В строке или столбце, соответствующем выбранному штрафу, для заполнения выбирается не вычеркнутая клетка с минимальным тарифом 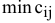 .
.
Если существует несколько одинаковых по величине максимальных штрафов в матрице, то в соответствующих строках или столбцах выбирается одна не вычеркнутая клетка с минимальным тарифом 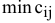 .
.
Если клеток с минимальным тарифом также несколько, то из них выбирается клетка 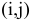 с максимальным суммарным штрафом, т.е. суммой штрафов по
с максимальным суммарным штрафом, т.е. суммой штрафов по 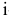 -й строке и
-й строке и 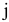 -му столбцу.
-му столбцу.
Формально и реальные и фиктивные столбцы и строки в транспортной матрице абсолютно равноправны. Поэтому при нахождении опорных планов фиктивные строки, столбцы и тарифы необходимо анализировать и использовать точно так же как и реальные. Но при вычислении значения ЦФ фиктивные перевозки не учитываются, поскольку они реально не были выполнены и оплачены.
Если величина фиктивных тарифов превышает максимальный из реальных тарифов задачи 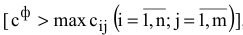 , то методы минимального элемента и Фогеля позволяют получить более дешевые планы перевозок, чем в случае с нулевыми фиктивными тарифами.
, то методы минимального элемента и Фогеля позволяют получить более дешевые планы перевозок, чем в случае с нулевыми фиктивными тарифами.
Задача № 5.01
Найти тремя методами опорный план ТЗ, в которой запасы на трех складах равны 210, 170, 65 ед. продукции, потребности четырех магазинов равны 125, 90, 130, 100 ед. продукции, тарифы перевозки в рублях за единицу продукции следующие:

Решение:
Проверка сбалансированности задачи показывает, что суммарный объем запасов равен суммарному объему потребностей, т.е. введение фиктивных столбцов или строк не потребуется
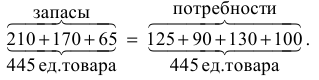
Результаты нахождения опорного плана различными методами представлены в табл. 5.1, 5.2 и 5.3.
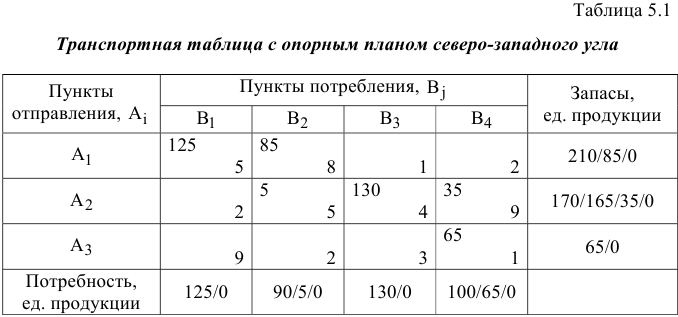
Опорный план 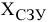 , найденный методом северо-западного угла
, найденный методом северо-западного угла

Соответствующая ЦФ (общие затраты на перевозку)
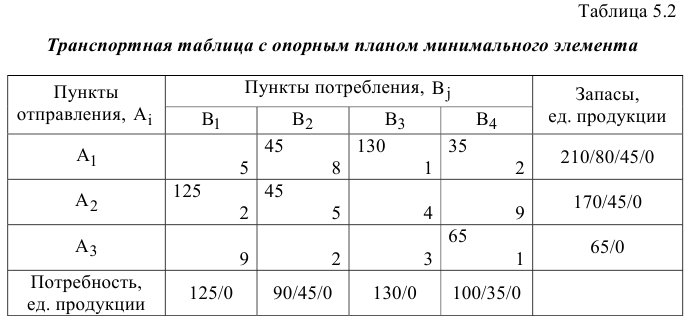
Опорный план 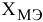 , найденный методом минимального элемента
, найденный методом минимального элемента
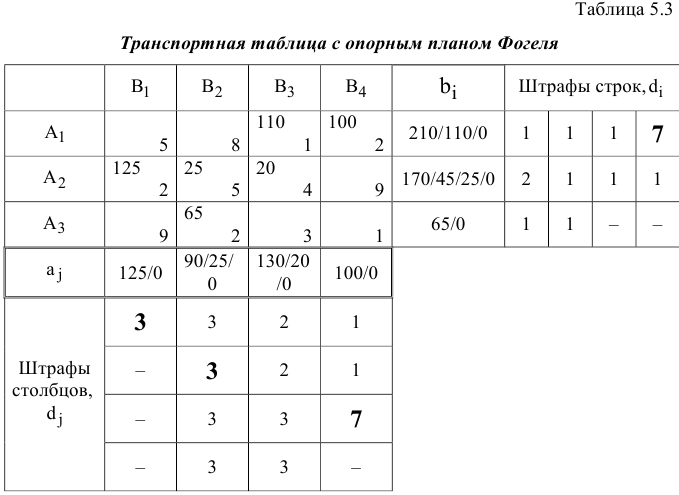
На первом шаге нахождения опорного плана методом Фогеля возникает ситуация равенства значений максимальных штрафов транспортной матрицы (см. табл. 5.3)
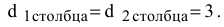
Минимальные тарифы в этих столбцах также совпадают
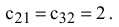
Поэтому необходимо сравнить суммарные штрафы 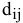 клеток (2,1) и (3,2)
клеток (2,1) и (3,2)
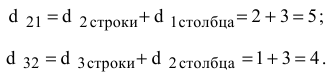
Т.к. 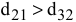 , то выбираем на первом шаге для заполнения клетку (2,1). Опорный план
, то выбираем на первом шаге для заполнения клетку (2,1). Опорный план 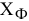 , найденный методом Фогеля
, найденный методом Фогеля
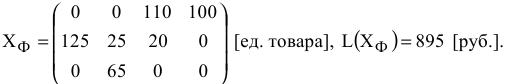
Общая распределительная задача линейного программирования
Общая распределительная задача ЛП — это РЗ, в которой работы и ресурсы (исполнители) выражаются в различных единицах измерения. Типичным примером такой задачи является организация выпуска разнородной продукции на оборудовании различных типов.
Исходные параметры модели РЗ
1) 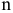 — количество исполнителей;
— количество исполнителей;
2) 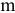 — количество видов выполняемых работ;
— количество видов выполняемых работ;
3) 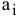 — запас рабочего ресурса исполнителя
— запас рабочего ресурса исполнителя 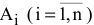 [ед. ресурса];
[ед. ресурса];
4) 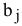 — план по выполнению работы
— план по выполнению работы 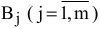 [ед. работ];
[ед. работ];
5) 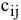 — стоимость выполнения работы
— стоимость выполнения работы 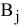 исполнителем
исполнителем 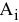 [руб./ед. работ];
[руб./ед. работ];
6) 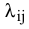 — интенсивность выполнения работы
— интенсивность выполнения работы 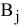 исполнителем
исполнителем 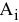 [ед. работ / ед. ресурса].
[ед. работ / ед. ресурса].
Искомые параметры модели РЗ
1) 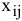 — планируемая загрузка исполнителя
— планируемая загрузка исполнителя 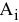 при выполнении работ
при выполнении работ 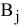 [ед. ресурса];
[ед. ресурса];
2) 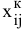 — количество работ
— количество работ 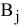 , которые должен будет произвести исполнитель
, которые должен будет произвести исполнитель 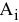 [ед. работ];
[ед. работ];
3) 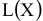 — общие расходы на выполнение всего запланированного объема работ [руб.].
— общие расходы на выполнение всего запланированного объема работ [руб.].
Этапы построения модели
I. Определение переменных.
II. Построение распределительной матрицы (см. табл. 6.1).
III. Задание ЦФ.
IV. Задание ограничений.

где 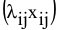 — это количество работ
— это количество работ 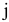 -го вида, выполненных
-го вида, выполненных 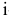 -м исполнителем.
-м исполнителем.
Этапы решения РЗ
I. Преобразование РЗ в ТЗ:
1) выбор базового ресурса и расчет нормированных производительностей ресурсов 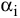 :
:
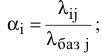
2) пересчет запаса рабочего ресурса исполнителей 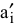 :
:
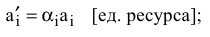
3) пересчет планового задания 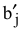 :
:
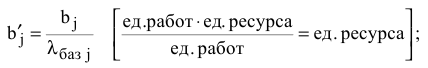
4) пересчет себестоимостей работ:
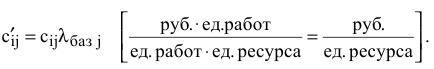
II. Проверка баланса пересчитанных параметров 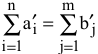 и построение транспортной матрицы.
и построение транспортной матрицы.
III. Поиск оптимального решения ТЗ 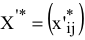 .
.
IV. Преобразование оптимального решения ТЗ 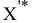 в оптимальное решение РЗ
в оптимальное решение РЗ 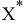 , причем переход
, причем переход 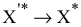 выполняется по формуле (6.6)
выполняется по формуле (6.6)
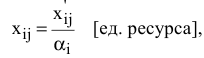
где 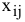 и
и 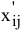 — соответственно элементы решения РЗ и ТЗ.
— соответственно элементы решения РЗ и ТЗ.
V. Определение количества работ 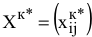 , соответствующее
, соответствующее
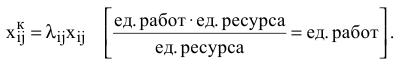
VI. Определение ЦФ распределительной задачи 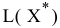 согласно (6.1).
согласно (6.1).
Задача № 6.01
На фабрике эксплуатируются три типа ткацких станков, которые могут выпускать четыре вида тканей. Известны следующие данные о производственном процессе:
• производительности станков по каждому виду ткани, м/ч

себестоимость тканей, руб./м
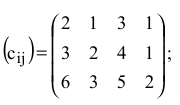
• фонды рабочего времени станков (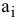 ): 90, 220, 180 ч;
): 90, 220, 180 ч;
• планируемый объем выпуска тканей (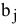 ): 1200, 900, 1800, 840 м.
): 1200, 900, 1800, 840 м.
Требуется распределить выпуск ткани по станкам с целью минимизации общей себестоимости производства ткани.
Решение:
Пусть переменные 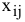 — это время, в течение которого
— это время, в течение которого 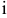 -й станок будет выпускать
-й станок будет выпускать  -ю ткань. Сведем исходные данные задачи в распределительную таблицу (табл. 6.2).
-ю ткань. Сведем исходные данные задачи в распределительную таблицу (табл. 6.2).
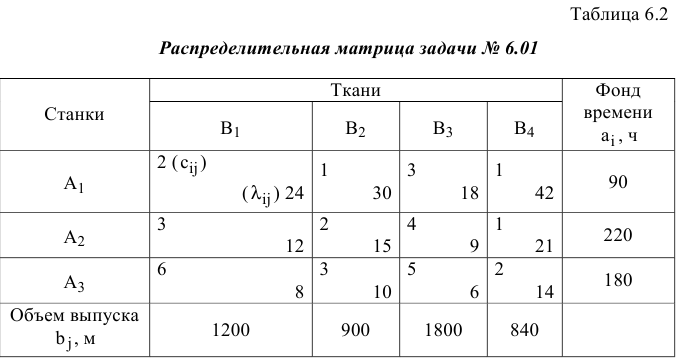
ЦФ имеет смысл себестоимости выпуска запланированного количества ткани всех видов
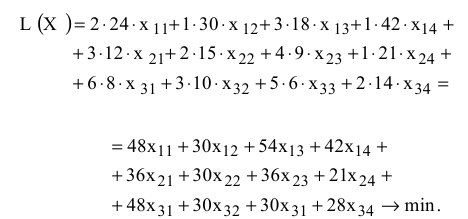
Ограничения имеют вид

Преобразуем РЗ в ТЗ, т.е. представим исходную задачу в виде, когда ткани производит только один станок — базовый и все параметры задачи согласуем с его характеристиками. В качестве базового можно выбирать любой из станков. Мы выберем станок с максимальной производительностью, т.е. 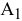 . По формуле (6.2) определим производительности станков
. По формуле (6.2) определим производительности станков 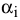 , нормированные относительно производительности базового станка:
, нормированные относительно производительности базового станка:
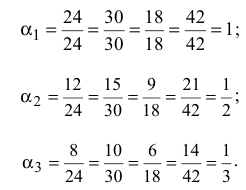
Таким образом, базовый станок работает в два раза быстрей второго станка и в три раза быстрей третьего.
Пересчитаем фонды времени станков по формуле (6.3):
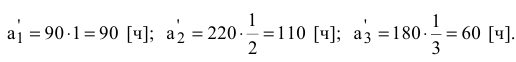
Из этих величин следует, что тот объем работ, который второй станок выполняет за свой фонд времени 220 ч базовый станок сможет выполнить за 110 ч. Аналогично объем работ, который третий станок выполняет за 180 ч базовый выполнит за 60 ч.
Пересчитаем плановое задание по формуле (6.4):
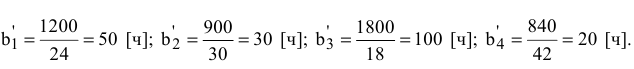
Отсюда следует, что план выпуска первого вида ткани базовый станок выполнит за 50 ч, второго вида — за 30 ч и т.д.
Пересчет себестоимостей производим по формуле (6.5), например:
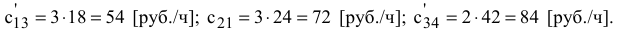
В полученной ТЗ условие баланса (4.2) не выполняется, т.к. суммарный фонд времени станков больше, чем это необходимо для выполнения плана по выпуску всех тканей (260 ч > 200 ч). Введем фиктивный столбец 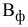 и запишем все пересчитанные параметры РЗ в транспортную матрицу (см. табл. 6.3). Фиктивные тарифы для упрощения приравняем к нулю.
и запишем все пересчитанные параметры РЗ в транспортную матрицу (см. табл. 6.3). Фиктивные тарифы для упрощения приравняем к нулю.
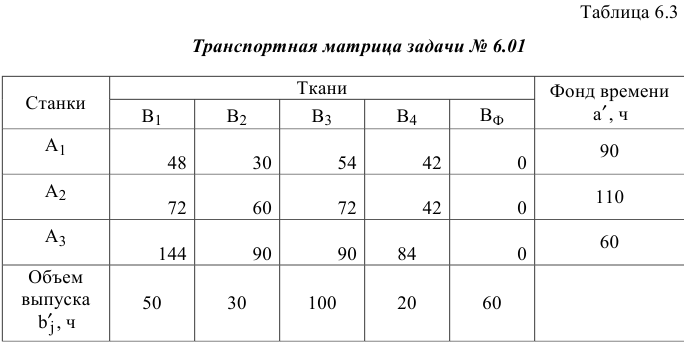
Для упрощения вместо оптимального решения рассмотрим опорный план  , найденный методом северо-западного угла.
, найденный методом северо-западного угла.

Преобразуем опорный план ТЗ  в опорный план РЗ
в опорный план РЗ  согласно (6.6)
согласно (6.6)

Таким образом, первый станок должен 50 ч производить ткань первого вида, 30 ч — ткань второго вида и 10 ч- ткань третьего вида. Второй станок должен 180 ч производить ткань третьего вида и 40 ч — ткань четвертого вида.  третий станок будет простаивать, не выпуская ткань вообще, т.к. согласно решению, его загрузка находится в фиктивном столбце
третий станок будет простаивать, не выпуская ткань вообще, т.к. согласно решению, его загрузка находится в фиктивном столбце 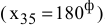
Определим, сколько метров ткани каждого вида должны произвести станки по формуле (6.7)

Определим общую себестоимость производства по формуле (6.1), используя вычисленные значения элементов матрицы 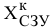
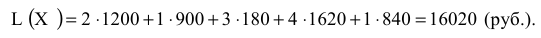
Сетевое планирование. Построение сетевых моделей
Построение сетевой модели (структурное планирование) начинается с разбиения проекта на четко определенные работы, для которых определяется продолжительность. Работа — это некоторый процесс, приводящий к достижению определенного результата, требующий затрат каких-либо ресурсов и имеющий протяженность во времени. По количеству затрачиваемого времени работа может быть:
• действительной, т.е. требующей затрат времени;
• фиктивной, т.е. формально не требующей затрат времени. Фиктивная работа может реально существовать, например, «передача документов от одного отдела к другому». Если продолжительность такой работы несоизмеримо мала по сравнению с продолжительностью других работ проекта, то формально ее принимают равной 0. Существуют фиктивные работы, которым в реальности не соответствуют никакие действия. Такие фиктивные работы только представляют связь между другими работами сетевой модели.
Работы связаны друг с другом таким образом, что выполнение одних работ может быть начато только после завершения некоторых других. Событие — это момент времени, когда завершаются одни работы и начинаются другие. Событие представляет собой результат проведенных работ и, в отличие от работ, не имеет протяженности во времени.
Взаимосвязь работ и событий, необходимых для достижения конечной цели проекта, изображается с помощью сетевого графика (сетевой модели). Работы изображаются стрелками, которые соединяют вершины, изображающие события. Начало и окончание любой работы описываются парой событий, которые называются начальным и конечным событиями.
Поэтому для указания конкретной работы используют код работы 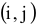 , состоящий из номеров начального (
, состоящий из номеров начального (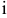 -го) и конечного (
-го) и конечного ( -го) событий (рис. 7.1).
-го) событий (рис. 7.1).
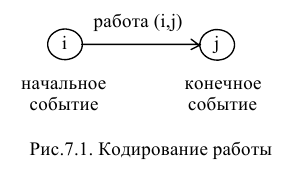
Любое событие может считаться наступившим только тогда, когда закончатся все входящие в него работы. Поэтому работы, выходящие из некоторого события, не могут начаться, пока не будут завершены все работы, входящие в это событие. Событие, не имеющее предшествующих ему событий, т.е. с которого начинается проект, называют исходным. Событие, которое не имеет последующих событий и отражает конечную цель проекта, называется завершающим.
Методические рекомендации по построению сетевых моделей
При построении сетевого графика необходимо следовать следующим правилам:
- длина стрелки не зависит от времени выполнения работы;
- стрелка может не быть прямолинейным отрезком;
- для действительных работ используются сплошные, а для фиктивных -пунктирные стрелки;
- каждая операция должна быть представлена только одной стрелкой;
- между одними и теми же событиями не должно быть параллельных работ, т.е. работ с одинаковыми кодами;
- следует избегать пересечения стрелок;
- не должно быть стрелок, направленных справа налево;
- номер начального события должен быть меньше номера конечного события;
- не должно быть висячих событий (т.е. не имеющих предшествующих событий), кроме исходного;
- не должно быть тупиковых событий (т.е. не имеющих последующих событий), кроме завершающего;
- не должно быть циклов (рис. 7.2).
Исходные данные для построения сетевой модели могут задаваться различными способами, например,
• описанием предполагаемого проекта. В этом случае необходимо самостоятельно разбить его на отдельные работы и установить их взаимные связи;
• списком работ проекта. В этом случае необходимо проанализировать содержание работ и установить существующие между ними связи;
• списком работ проекта с указанием их упорядочения. В этом случае необходимо только отобразить работы на сетевом графике.
Построение сетевого графика необходимо начинать с выявления исходных работ модели. Если согласно условию некоторая работа может выполняться, не ожидая окончания каких-либо других работ, то такая работа является исходной в сетевой модели и ее начальным событием является исходное событие. Если исходных работ несколько, то их стрелки выходят все из одного исходного события.
Если, согласно условию, после окончания некоторой работы не должны выполняться никакие другие работы, то такая работа является завершающей работой сетевой модели и ее конечным событием является завершающее событие. Если завершающих исходных работ несколько, то их стрелки заходят все в одно завершающее событие.
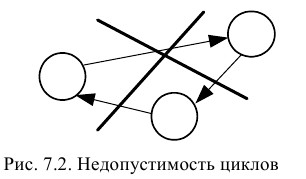
Если, согласно условию, несколько работ имеют общее начальное и общее конечное события, то они являются параллельными, имеют одинаковый код, что недопустимо. Для устранения параллельности работ вводят дополнительное событие и фиктивную работу (которой в реальности не соответствует никакое действие) таким образом, чтобы конечные события работ различались (рис. 7.3.).
Задача № 7.01
Постройте сетевую модель программы опроса общественного мнения, которая включает разработку (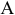 ; 1 день) и распечатку анкет (
; 1 день) и распечатку анкет (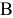 ; 0,5 дня), прием на работу (
; 0,5 дня), прием на работу (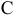 ; 2 дня) и обучение (
; 2 дня) и обучение (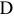 ; 2 дня) персонала, выбор опрашиваемых лиц (
; 2 дня) персонала, выбор опрашиваемых лиц (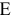 ; 2 дня), рассылку им анкет (
; 2 дня), рассылку им анкет (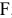 ; 1 день) и анализ полученных данных (
; 1 день) и анализ полученных данных (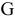 ; 5 дней).
; 5 дней).
Решение:
Из условия задачи нам известно содержание работ, но явно не указаны взаимосвязи между работами. Поэтому для их установления необходимо проанализировать смысл каждой конкретной работы и выяснить, какие из остальных работ должны ей непосредственно предшествовать. Исходной работой, начинающей сетевой график, в данном случае является «прием на работу» (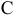 ), поскольку все остальные работы должны выполняться уже принятыми на работу сотрудниками (рис. 7.4). Перед выполнением всех работ по опросу общественного мнения сотрудников необходимо обучить персонал (
), поскольку все остальные работы должны выполняться уже принятыми на работу сотрудниками (рис. 7.4). Перед выполнением всех работ по опросу общественного мнения сотрудников необходимо обучить персонал (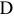 ). Перед тем как разослать анкеты (
). Перед тем как разослать анкеты (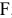 ), их надо разработать (
), их надо разработать (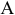 ), распечатать (
), распечатать (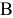 ) и выбрать опрашиваемых лип (
) и выбрать опрашиваемых лип (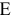 ), причем работу с анкетами и выбор лиц можно выполнять одновременно. Завершающей работой проекта является анализ полученных данных (
), причем работу с анкетами и выбор лиц можно выполнять одновременно. Завершающей работой проекта является анализ полученных данных (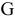 ), который нельзя выполнить без предварительной рассылки анкет (
), который нельзя выполнить без предварительной рассылки анкет (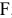 ). В результате этих рассуждений построим сетевую модель и пронумеруем события модели (см. рис. 7.4).
). В результате этих рассуждений построим сетевую модель и пронумеруем события модели (см. рис. 7.4).
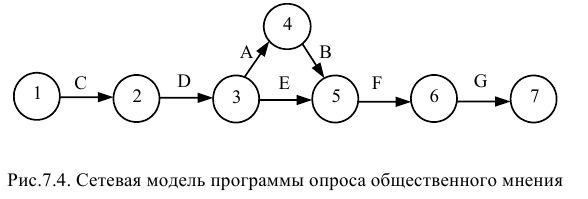
Задача № 7.02
Постройте сетевую модель, включающую работы  , которая отображает следующее упорядочение работ:
, которая отображает следующее упорядочение работ:
1)  и
и 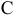 — исходные операции проекта;
— исходные операции проекта;
2) 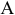 и
и 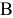 предшествуют
предшествуют 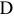 ;
;
3) 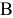 предшествует
предшествует 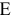 ,
, 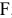 и
и 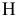 ;
;
4) 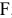 и
и 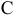 предшествует
предшествует  ;
;
5)  и
и  предшествуют
предшествуют  и
и 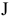 ;
;
6) 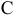 ,
, 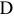 ,
, 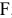 и
и 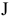 предшествуют
предшествуют 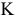 ;
;
7) 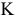 предшествует
предшествует 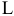 .
.
Решение:
В пункте 1) условия явно указано, что 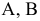 и
и 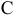 являются исходными работами, поэтому изобразим их тремя стрелками, выходящими из исходного события 1. Пункт 2) условия означает, что стрелки работ
являются исходными работами, поэтому изобразим их тремя стрелками, выходящими из исходного события 1. Пункт 2) условия означает, что стрелки работ 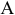 и
и 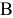 должны окончиться в одном событии, из которого выйдет стрелка работы
должны окончиться в одном событии, из которого выйдет стрелка работы 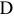 . Но поскольку стрелки работ
. Но поскольку стрелки работ 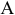 и
и 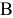 также и начинаются в одном событии, то имеет место параллельность работ, которая недопустима правилами построения сетевых моделей (см. рис. 7.5).
также и начинаются в одном событии, то имеет место параллельность работ, которая недопустима правилами построения сетевых моделей (см. рис. 7.5).
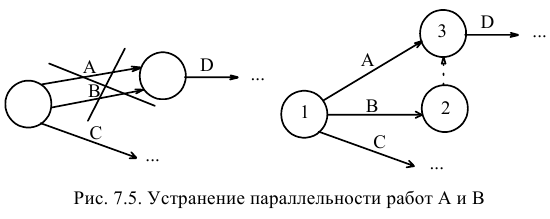
Для ее устранения введем дополнительное событие 2, в которое войдет работа 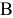 , после чего соединим события 2 и 3, в которые входят работы
, после чего соединим события 2 и 3, в которые входят работы 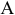 и
и 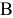 пунктирной стрелкой фиктивной работы. В данном случае фиктивная работа (2,3) не соответствует никакой реальной работе, а лишь отображает логическую связь между работами
пунктирной стрелкой фиктивной работы. В данном случае фиктивная работа (2,3) не соответствует никакой реальной работе, а лишь отображает логическую связь между работами 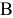 и
и  . Дальнейшее построение рассмотрим с помощью рис. 7.6.
. Дальнейшее построение рассмотрим с помощью рис. 7.6.
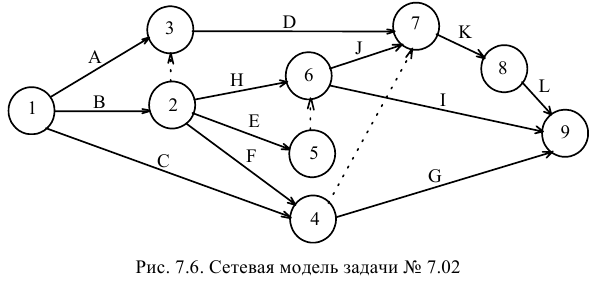
Согласно пункту 3) условия задачи из события 2, выходят три стрелки работ  ,
,  и
и 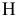 . Согласно пункту 4) условия задачи стрелки работ
. Согласно пункту 4) условия задачи стрелки работ 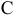 и
и 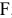 должны войти в общее событие, из которого выйдет стрелка работы
должны войти в общее событие, из которого выйдет стрелка работы 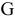 . Проблема с параллельностью работ
. Проблема с параллельностью работ 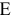 и
и 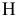 [пункт 5) условия задачи] решается путем введения дополнительного события 5 и фиктивной работы (5,6). Для отображения в сетевой модели пункта 6) условия задачи введем стрелки работ
[пункт 5) условия задачи] решается путем введения дополнительного события 5 и фиктивной работы (5,6). Для отображения в сетевой модели пункта 6) условия задачи введем стрелки работ 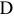 и
и 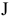 в событие 7, а связь работ
в событие 7, а связь работ 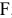 и
и 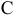 с работой
с работой 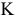 отобразим с помощью фиктивной работы (4,7). Стрелки работ
отобразим с помощью фиктивной работы (4,7). Стрелки работ 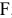 и
и 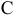 нельзя было напрямую вводить в событие 7, потому что после них должна следовать работа
нельзя было напрямую вводить в событие 7, потому что после них должна следовать работа 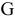 , которая с работами
, которая с работами 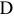 и
и 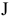 никак не связана. Стрелка работы
никак не связана. Стрелка работы 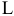 выходит из события 8, т.е. после окончания работы
выходит из события 8, т.е. после окончания работы 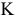 в соответствии с пунктом 7) условия задачи.
в соответствии с пунктом 7) условия задачи.
Поскольку в условии не указано, что работы 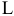 ,
, 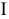 и
и  предшествуют каким-либо другим работам, то эти работы являются завершающими и их стрелки войдут в завершающее событие 9. Нумерацию событий проводят после построения сетевого графика, следя за тем, чтобы номер начального события каждой работы был меньше номера ее конечного события.
предшествуют каким-либо другим работам, то эти работы являются завершающими и их стрелки войдут в завершающее событие 9. Нумерацию событий проводят после построения сетевого графика, следя за тем, чтобы номер начального события каждой работы был меньше номера ее конечного события.
Расчет и анализ сетевых моделей
Календарное планирование предусматривает определение моментов начала и окончания каждой работы и других временных характеристик сетевого графика. Это позволяет проанализировать сетевую модель, выявить критические работы, непосредственно определяющие срок выполнения проекта, провести оптимизацию использования ресурсов (временных, финансовых, исполнителей).
Расчет сетевой модели начинают с временных параметров событии, которые вписывают непосредственно в вершины сетевого графика (рис. 8.1):
• 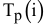 — ранний срок наступления события
— ранний срок наступления события  , минимально необходимый для выполнения всех работ, которые предшествуют событию
, минимально необходимый для выполнения всех работ, которые предшествуют событию  ;
;
• 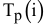 — поздний срок наступления события
— поздний срок наступления события 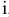 , превышение которого вызовет аналогичную задержку наступления завершающего события сети;
, превышение которого вызовет аналогичную задержку наступления завершающего события сети;
• 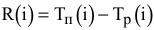 — резерв события
— резерв события 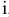 , т.е. время, на которое может быть отсрочено наступление события
, т.е. время, на которое может быть отсрочено наступление события  без нарушения сроков завершения проекта в целом.
без нарушения сроков завершения проекта в целом.
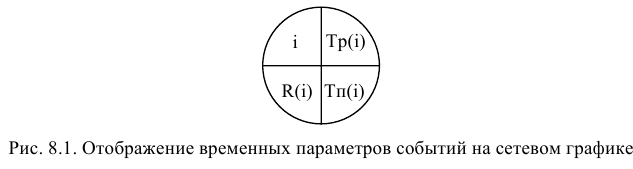
Ранние сроки свершения событий 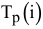 рассчитываются от исходного (И)
рассчитываются от исходного (И)
к завершающему (3) событию следующим образом:
1) для исходного события И 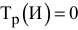 ;
;
2) для всех остальных событий I
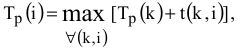
где максимум берется по всем работам 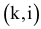 , входящим в событие
, входящим в событие 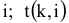 — длительность» работы
— длительность» работы 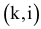 (рис. 8.2).
(рис. 8.2).
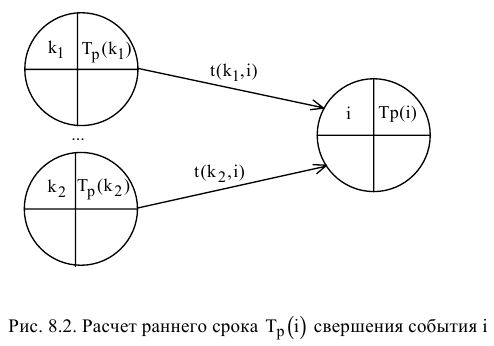
Поздние сроки свершения событий 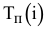 рассчитываются от завершающего к исходному событию:
рассчитываются от завершающего к исходному событию:
1) для завершающего события 3 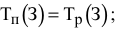
2) для всех остальных событий
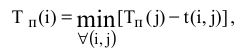
где минимум берется по всем работам 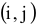 , выходящим из события
, выходящим из события 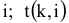 — длительность работы
— длительность работы 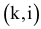
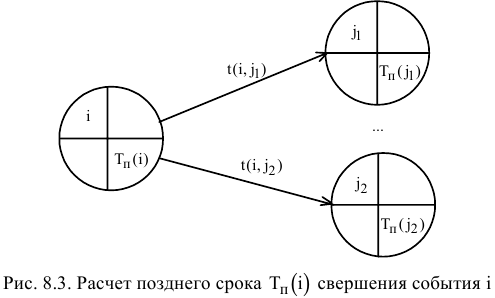
Временные параметры работ определяются на основе ранних и поздних сроков событий:

максимальное время, на которое можно увеличить длительность работы 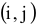 или отсрочить ее начало, чтобы не нарушился срок завершения проекта в целом;
или отсрочить ее начало, чтобы не нарушился срок завершения проекта в целом;
• 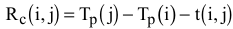 — свободный резерв работы показывает
— свободный резерв работы показывает
максимальное время, на которое можно увеличить продолжительность работы 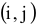 или отсрочить ее начало, не меняя ранних сроков начала последующих работ.
или отсрочить ее начало, не меняя ранних сроков начала последующих работ.
Путь — это последовательность работ в сетевом графике (в частном случае это одна работа), в которой конечное событие одной работы совпадает с начальным событием следующей за ней работы. Полный путь — это путь от исходного до завершающего события. Критический путь — максимальный по продолжительности полный путь. Работы, лежащие на критическом пути, называют критическими. Критические работы имеют нулевые свободные и полные резервы. Подкритический путь — полный путь, ближайший по длительности к критическому пути.
Для проведения анализа временных параметров сетевой модели используют график привязки, который отображает взаимосвязь выполняемых работ во времени. По вертикальной оси графика привязки откладываются коды работ, по горизонтальной оси — отрезки, соответствующие длительностям работ (раннее начало и раннее окончание работ). График привязки можно построить на основе данных о продолжительности работ. При этом необходимо помнить, что работа 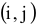 может выполняться только после того как будут выполнены все предшествующие ей работы
может выполняться только после того как будут выполнены все предшествующие ей работы 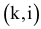 .
.
Задача № 8.01
Компания разрабатывает строительный проект. Исходные данные по основным операциям проекта представлены в табл. 8.1. Постройте сетевую модель проекта, определите критические пути модели и проанализируйте, как влияет на ход выполнения проекта задержка работы 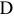 на 4 недели.
на 4 недели.
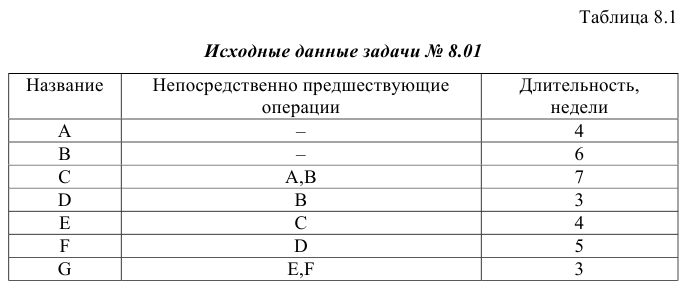
Решение:
Построим сетевую модель и рассчитаем временные параметры событий (рис. 8.3). При поиске критических путей на сетевом графике будем использовать следующие условия его критичности:
• необходимое условие- нулевые резервы событий, лежащих на крит ическом нут и;
• достаточное условие — нулевые полные резервы работ, лежащих на крит ическом нут и.
Согласно необходимому условию два полных пути сетевой модели (см. рис. 8.3)
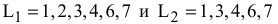
могут быть критическими. Проверим достаточное условие критичности для работ (1,2) и (1,3)
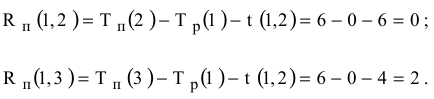
Путь 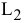 , начинающийся с работы (1,3) не является критическим, т.к. как минимум одна из его работ (1,3) не является критической. Работа (1,3) имеет ненулевой полный резерв, а значит может быть задержана с выполнением, что недопустимо для критических работ.
, начинающийся с работы (1,3) не является критическим, т.к. как минимум одна из его работ (1,3) не является критической. Работа (1,3) имеет ненулевой полный резерв, а значит может быть задержана с выполнением, что недопустимо для критических работ.
Таким образом, сетевая модель имеет единственный критический путь 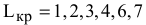 длительностью
длительностью 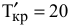 недель. За выполнением работ этого пути необходим особый контроль, т.к. любое увеличение их длительности нарушит срок выполнения проекта в целом.
недель. За выполнением работ этого пути необходим особый контроль, т.к. любое увеличение их длительности нарушит срок выполнения проекта в целом.
Работа  или (2,5) не является критической, ее полный резерв равен 3-м неделям. Это означает, что при задержке работы в пределах 3-х недель срок выполнения проекта не будет нарушен. Поэтому если согласно условию работа
или (2,5) не является критической, ее полный резерв равен 3-м неделям. Это означает, что при задержке работы в пределах 3-х недель срок выполнения проекта не будет нарушен. Поэтому если согласно условию работа  задержится на 4 недели, то весь проект закончится на 1 неделю позже.
задержится на 4 недели, то весь проект закончится на 1 неделю позже.
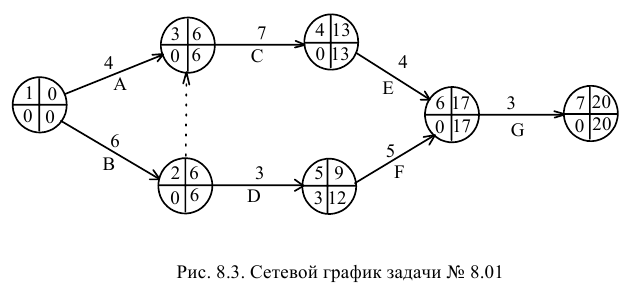
Задача № 8.02
По данным о кодах и длительностях работ в днях (табл. 8.2) постройте график привязки сетевой модели, определите критические пути и их длительность. Определите свободные и полные резервы каждой работы, отметьте на графике привязки свободные резервы работ.

Общие рекомендации
При поиске критических путей следует помнить, что признаком критической работы являются нулевые значения резервов времени. Это означает, что каждая последующая критическая работа будет начинаться строго в момент окончания предыдущей критической работы. Вследствие этого сдвиг любой из работ критического пути обязательно приведет к увеличению первоначальной длительности проекта (Ткр). Кроме того, следует
учесть, что критический путь является полным, т.е. соединяет исходное и завершающее события сети. Поэтому на графике привязки первая из работ критического пути всегда начинается в исходном событии сети с нулевого (начального) момента времени, а последняя из работ критического пути всегда завершается позже всех остальных работ сети в завершающем событии.
Из вышеприведенных соображений следует способ определения критического пути на графике привязки (все найденные работы выписываются последовательно справа налево)’.
1) найти на графике привязки и выписать работу 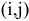 , которая заканчивается позже всех остальных. Это будет последняя работа критического пути (ее конечное событие иметь номер завершающего события сети);
, которая заканчивается позже всех остальных. Это будет последняя работа критического пути (ее конечное событие иметь номер завершающего события сети);
2) из всех работ сети 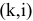 , конечное событие которых
, конечное событие которых 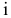 совпадает с начальным событием
совпадает с начальным событием 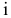 работы
работы 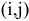 , найденной в п. 1), выбрать и выписать ту, которая на графике вплотную примыкает к работе
, найденной в п. 1), выбрать и выписать ту, которая на графике вплотную примыкает к работе 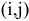 ;
;
3) из всех работ сети 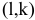 , конечное событие которых к совпадает с начальным событием
, конечное событие которых к совпадает с начальным событием 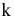 работы
работы 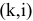 , найденной в п. 2), выбрать и выписать ту, которая на графике вплотную примыкает к работе
, найденной в п. 2), выбрать и выписать ту, которая на графике вплотную примыкает к работе  ;
;
4) продолжать п. 3) до тех пор, пока не будет найдена исходная работа сети, т.е. начинающаяся в нулевой момент времени (ее начальное событие будет иметь номер исходного события сети, например, 1).
Следует заметить, что если в сетевой модели несколько критических путей, то, выполняя вышеописанные действия, можно обнаружить несколько работ, удовлетворяющих сформулированным требованиям. В таком случае необходимо продолжать поиск по каждой из таких работ в отдельности. В сложных сетевых моделях подобные разветвления могут привести к большим затратам времени на поиск критически путей. Тем не менее, такой способ хорош для учебных целей, поскольку дает понимание значения критических работ в сетевой модели и учит «читать» и понимать график привязки.
Решение:
I. Поиск критических путей
1) Построим график привязки (рис. 8.4).
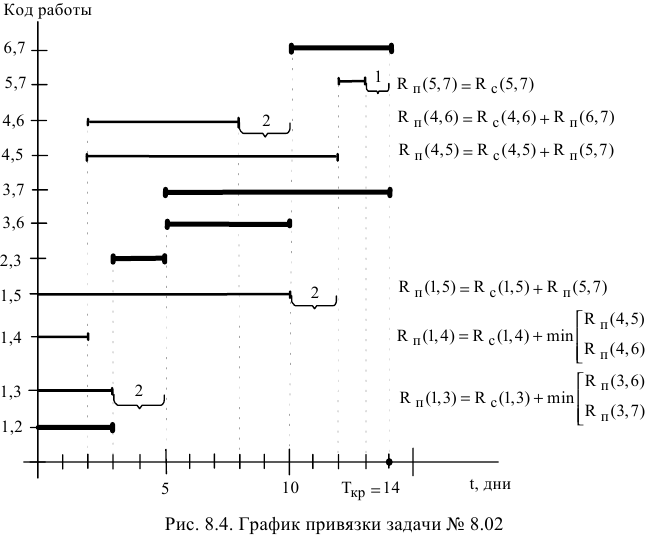
2) Начнем поиск критических путей (справа налево) с работ, завершающих проект. На графике привязки (см. рис. 8.4) две работы (6,7) и (3,7), которые заканчиваются позже остальных в завершающем событии № 7. Записываем работы, определенные как критические справа налево
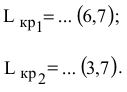
3) Найдем критическую работу из 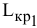 , предшествующую (6,7). Код этой работы должен оканчиваться на 6. Таких работ две — (4,6) и (3,6). Но только одна из них, работа (3,6) по времени своего окончания вплотную «примыкает» на графике к началу работы (6,7). Допишем слева найденную критическую работу (3,6) к выражению (8.1)
, предшествующую (6,7). Код этой работы должен оканчиваться на 6. Таких работ две — (4,6) и (3,6). Но только одна из них, работа (3,6) по времени своего окончания вплотную «примыкает» на графике к началу работы (6,7). Допишем слева найденную критическую работу (3,6) к выражению (8.1)
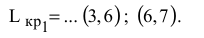
4) Найдем критическую работу из 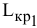 , предшествующую (3,6). Код этой работы должен оканчиваться на 3. Таких работ две — (2,3) и (1,3). Но только одна из них, работа (2,3) по времени своего окончания вплотную «примыкает» на графике к началу работы (3,6). Допишем слева найденную критическую работу (2,3) к выражению (8.2)
, предшествующую (3,6). Код этой работы должен оканчиваться на 3. Таких работ две — (2,3) и (1,3). Но только одна из них, работа (2,3) по времени своего окончания вплотную «примыкает» на графике к началу работы (3,6). Допишем слева найденную критическую работу (2,3) к выражению (8.2)
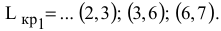
5) Найдем критическую работу из 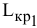 , предшествующую (2,3). Код этой работы должен оканчиваться на 2. Работа (1,2) по времени своего окончания вплотную «примыкает» на графике к началу работы (2,3). С этой работы начинается критический путь
, предшествующую (2,3). Код этой работы должен оканчиваться на 2. Работа (1,2) по времени своего окончания вплотную «примыкает» на графике к началу работы (2,3). С этой работы начинается критический путь 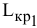
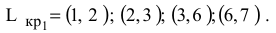
6) Аналогичный поиск работ критического пути 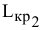 приводит к результату
приводит к результату
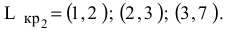
В другой форме записи
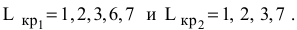
7) Для наглядности выделим на графике привязки критические работы жирной линией.
II. Поиск резервов работ
1) Для всех найденных критических работ впишем в табл.3 нулевые значения свободного и полного резервов. Рассмотрим некритические работы, начиная с конца табл. 8.3.
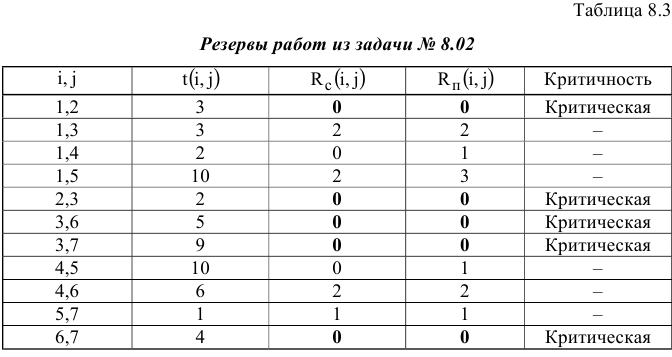
2) Работа (5,7), согласно графику привязки (см. рис. 8.4) заканчивается в 13-й день, а завершающее событие 7 сети, в которое она входит, наступает лишь в 14-й день. Т.е. если работа (5,7) задержится на 1 день, то это не повлияет на срок выполнения проекта 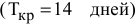 . Поскольку (5,7) завершающая работа сети, то ее полный и свободный резервы равны
. Поскольку (5,7) завершающая работа сети, то ее полный и свободный резервы равны
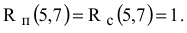
3) Работа (4,6) заканчивается в 8-й день, в то время как последующая работа (6,7) начинается в 10-й день. То есть, работа (4,6) может задержаться на 2 дня и это никак не повлияет на время начала последующей работы (6,7), т.е.
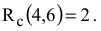
Правило А№ 8.1
Полный резерв любой работы складывается из собственного свободного резерва и минимального из полных резервов непосредственно следующих работ.
За работой (4,6) следует только критическая работа (6,7) с нулевым полным резервом. Поэтому
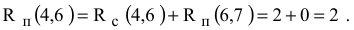
4) Работа (4,5) заканчивается в 12-й день, в этот же день начинается следующая работа (5,7), т.е. любая задержка выполнения работы (4,5) приведет к задержке начала работы (5,7). Это означает, что работа (4,5) не имеет свободного резерва 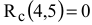 . Но если сдвинуть во времени работу (4,5) на 1 день, то работа (5,7) также сдвинется на 1 день и это не нарушит срок выполнения проекта, т.к. у работы (5,7) есть временной резерв. Таким образом согласно правилу № 8.1
. Но если сдвинуть во времени работу (4,5) на 1 день, то работа (5,7) также сдвинется на 1 день и это не нарушит срок выполнения проекта, т.к. у работы (5,7) есть временной резерв. Таким образом согласно правилу № 8.1
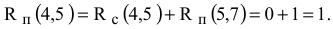
5) Работа (1,5) заканчивается в 10-й день, в то время как последующая работа (5,7) начинается в 12-й день. Т.е. работа (1,5) может задержаться на 2 дня и это никак не повлияет на время начала последующей работы (5,7), т.е. 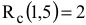 . Кроме того, поскольку последующая работа (5,7) имеет резерв в 1 день, то, в общем, работу (1,5) можно сдвинуть на 3 дня и это не нарушит сроков проекта (см. рис. 8.4), т.е.
. Кроме того, поскольку последующая работа (5,7) имеет резерв в 1 день, то, в общем, работу (1,5) можно сдвинуть на 3 дня и это не нарушит сроков проекта (см. рис. 8.4), т.е.
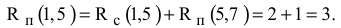
6) Работа (1,4) заканчивается во 2-й день, и в этот же день начинаются следующие работы (4,5) и (4,6). Т.е. работа (1,4) не имеет свободного резерва времени 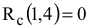 . Поскольку после работы (1,4) следуют две работы с различными полными резервами, то согласно правилу № 8.1
. Поскольку после работы (1,4) следуют две работы с различными полными резервами, то согласно правилу № 8.1
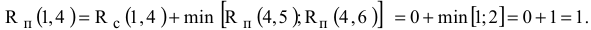
7) Работа (1,3) заканчивается в 3-й день, а следующие за ней работы (3,6) и (3,7) начинаются в 5-й день, т.е. 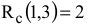 . Поскольку обе последующие работы критические, то полный и свободный резерв работы (1,3) совпадают
. Поскольку обе последующие работы критические, то полный и свободный резерв работы (1,3) совпадают
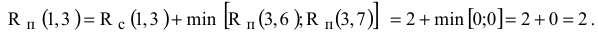
8) Ненулевые свободные резервы работ обозначены на графике привязки фигурными скобками (см. рис. 8.4).
Регрессионный и корреляционный анализ
Регрессионный и корреляционный анализ позволяет установить и оценить зависимость изучаемой случайной величины  от одной или нескольких других величин
от одной или нескольких других величин  , и делать прогнозы значений
, и делать прогнозы значений 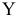 . Параметр
. Параметр 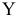 , значение которого нужно предсказывать, является зависимой переменной. Параметр
, значение которого нужно предсказывать, является зависимой переменной. Параметр 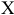 , значения которого нам известны заранее и который влияет на значения
, значения которого нам известны заранее и который влияет на значения 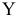 , называется независимой переменной. Например,
, называется независимой переменной. Например, 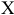 — количество внесенных удобрений,
— количество внесенных удобрений, 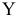 — снимаемый урожай;
— снимаемый урожай; 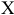 — величина затрат компании на рекламу своего товара,
— величина затрат компании на рекламу своего товара, 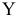 — объем продаж этого товара и т.д.
— объем продаж этого товара и т.д.
Корреляционная зависимость 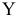 от
от 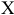 — это функциональная зависимость
— это функциональная зависимость
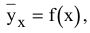
где 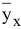 — среднее арифметическое (условное среднее) всех возможных значений параметра
— среднее арифметическое (условное среднее) всех возможных значений параметра 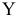 , которые соответствуют значению
, которые соответствуют значению 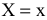 . Уравнение (9.1) называется уравнением регрессии
. Уравнение (9.1) называется уравнением регрессии 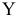 на
на 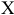 , функция
, функция 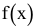 — регрессией
— регрессией 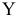 на
на 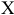 , а ее график — линией регрессии
, а ее график — линией регрессии 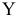 на
на  .
.
Основная задача регрессионного анализа — установление формы корреляционной связи, т.е. вида функции регрессии (линейная, квадратичная, показательная и т.д.).
Метод наименьших квадратов позволяет определить коэффициенты уравнения регрессии таким образом, чтобы точки, построенные по исходным данным 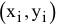 , лежали как можно ближе к точкам линии регрессии (9.1).
, лежали как можно ближе к точкам линии регрессии (9.1).
Формально это записывается как минимизация суммы квадратов отклонений (ошибок) функции регрессии и исходных точек
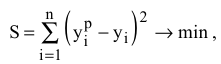
где 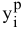 — значение, вычисленное по уравнению регрессии;
— значение, вычисленное по уравнению регрессии; 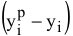 —отклонение
—отклонение 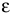 (ошибка, остаток) (рис. 9.1);
(ошибка, остаток) (рис. 9.1); 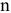 — количество пар исходных данных.
— количество пар исходных данных.
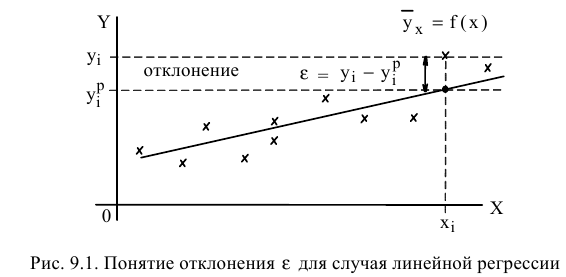
В регрессионном анализе предполагается, что математическое ожидание случайной величины 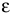 равно нулю и ее дисперсия одинакова для всех наблюдаемых значений
равно нулю и ее дисперсия одинакова для всех наблюдаемых значений 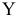 . Отсюда следует, что рассеяние данных возле линии регрессии должно быть одинаково при всех значениях параметра
. Отсюда следует, что рассеяние данных возле линии регрессии должно быть одинаково при всех значениях параметра 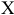 . В случае, показанном на рис. 9.2 данные распределяются вдоль линии регрессии неравномерно, поэтому метод наименьших квадратов в этом случае неприменим.
. В случае, показанном на рис. 9.2 данные распределяются вдоль линии регрессии неравномерно, поэтому метод наименьших квадратов в этом случае неприменим.
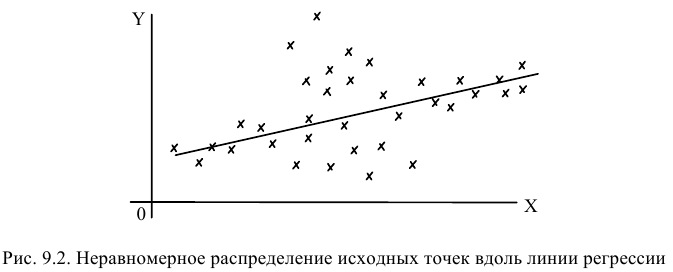
Основная задача корреляционного анализа — оценка тесноты (силы) корреляционной связи. Теснота корреляционной зависимости 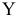 от
от 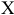 оценивается по величине рассеяния значений параметра
оценивается по величине рассеяния значений параметра 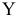 вокруг условного среднего
вокруг условного среднего 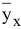 . Большое рассеяние говорит о слабой зависимости
. Большое рассеяние говорит о слабой зависимости 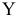 от
от 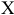 , либо об ее отсутствии и, наоборот, малое рассеяние указывает на наличие достаточно сильной зависимости.
, либо об ее отсутствии и, наоборот, малое рассеяние указывает на наличие достаточно сильной зависимости.
Коэффициент детерминации 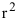 показывает, на сколько процентов (
показывает, на сколько процентов (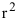 100%) найденная функция регрессии описывает связь между исходными значениями параметров
100%) найденная функция регрессии описывает связь между исходными значениями параметров 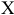 и
и 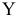
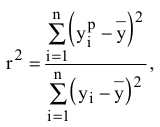
где 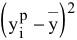 — объясненная вариация;
— объясненная вариация; 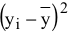 — общая вариация (рис. 9.3).
— общая вариация (рис. 9.3).
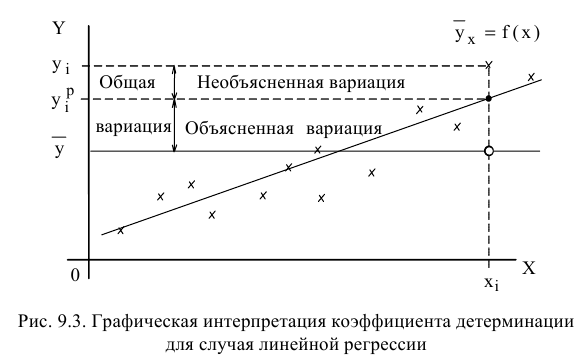
Соответственно, величина (1-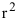 )100% показывает, сколько процентов вариации параметра
)100% показывает, сколько процентов вариации параметра 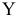 обусловлены факторами, не включенными в регрессионную модель. При высоком (
обусловлены факторами, не включенными в регрессионную модель. При высоком (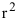 >75%) значении коэффициента детерминации можно делать прогноз
>75%) значении коэффициента детерминации можно делать прогноз 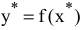 для конкретного значения
для конкретного значения 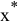 .
.
Для проведения регрессионного анализа и прогнозирования необходимо:
1) построить график исходных данных и попытаться зрительно, приближенно определить характер зависимости;
2) выбрать вид функции регрессии, которая может описывать связь исходных данных;
3) определить численные коэффициенты функции регрессии;
4) оценить силу найденной регрессионной зависимости на основе коэффициента детерминации 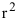 ;
;
5) сделать прогноз (при 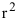 >75%) или сделать вывод о невозможности прогнозирования с помощью найденной регрессионной зависимости. При этом не рекомендуется использовать модель регрессии для тех значений независимого параметра
>75%) или сделать вывод о невозможности прогнозирования с помощью найденной регрессионной зависимости. При этом не рекомендуется использовать модель регрессии для тех значений независимого параметра 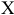 , которые не принадлежат интервалу, заданному в исходных данных.
, которые не принадлежат интервалу, заданному в исходных данных.
Линейная регрессии
Коэффициенты линейной регрессии 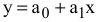 вычисляются по следующим формулам (все суммы берутся по
вычисляются по следующим формулам (все суммы берутся по 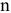 парам исходных данных)
парам исходных данных)
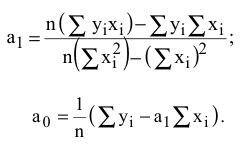
Для удобства вычислений используют вспомогательную таблицу (табл. 9.1), в которой рассчитываются необходимые суммы.

Задача№ 9.01
Некоторая фирма занимается поставками различных грузов на короткие расстояния внутри города. Перед менеджером стоит задача оценить стоимость таких услуг, зависящую от затрачиваемого на поставку времени. В качестве наиболее важного фактора, влияющего на время поставки, менеджер выбрал пройденное расстояние. Были собраны исходные данные о десяти поставках (табл. 9.2).

Постройте график исходных данных, определите по нему характер зависимости между расстоянием и затраченным временем, проанализируйте применимость метода наименьших квадратов, постройте уравнение регрессии, проанализируйте силу регрессионной связи и сделайте прогноз времени поездки на 2 мили.
Решение:
На рис. 9.4 построены исходные данные по десяти поездкам.
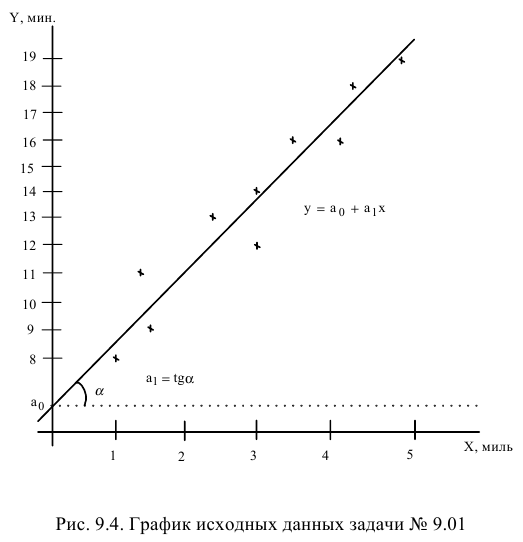
Помимо расстояния на время поставки влияют пробки на дорогах, время суток, дорожные работы, погода, квалификация водителя, вид транспорта. Построенные точки не находятся точно на линии, что обусловлено описанными выше факторами. Но эти точки собраны вокруг прямой линии, поэтому можно предположить линейную связь между параметрами. Все исходные точки равномерно распределены вдоль предполагаемой прямой линии, что позволяет применить метод наименьших квадратов.
Вычислим суммы, необходимые для расчета коэффициентов линейной регрессии, коэффициента детерминации с помощью табл. 9.3.
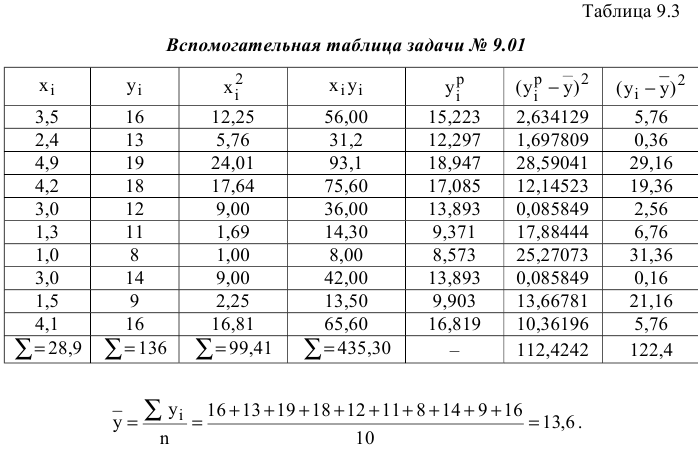
По формулам (9.3) вычислим коэффициенты линейной регрессии

Таким образом, искомая регрессионная зависимость имеет вид
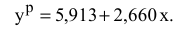
Наклон линии регрессии 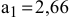 минут на милю — это количество минут, приходящееся на одну милю расстояния. Координата точки пересечения прямой с осью
минут на милю — это количество минут, приходящееся на одну милю расстояния. Координата точки пересечения прямой с осью 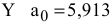 минут — это время, которое не зависит от пройденного расстояния, а обуславливается всеми остальными возможными факторами, явно не учтенными при анализе.
минут — это время, которое не зависит от пройденного расстояния, а обуславливается всеми остальными возможными факторами, явно не учтенными при анализе.
По формуле (9.2) вычислим коэффициент детерминации
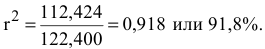
Таким образом, линейная модель объясняет 91,8% вариации времени доставки. Не объясняется 100% — 91,8% = 8,2% вариации времени поездки, которые обусловлены остальными факторами, влияющими на время поставки, но не включенными в линейную модель регрессии.
Поскольку коэффициент детерминации имеет достаточно высокое значение и расстояние 2 мили, для которого надо сделать прогноз, находится в пределах диапазона исходных данных (см. табл. 9.2), то мы можем использовать полученное уравнение линейной регрессии (9.4) для прогнозирования
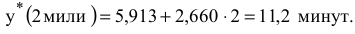
При прогнозах на расстояния, не входящие в диапазон исходных данных, нельзя гарантировать справедливость модели (9.4). Это объясняется тем, что связь между временем и расстоянием может изменяться по мере увеличения расстояния. На время дальних перевозок могут влиять новые факторы такие, как использование скоростных шоссе, остановки на отдых, обед и т.п.
Приблизительным, но самым простым и наглядным способом проверки удовлетворительности регрессионной модели является графическое представление отклонений (рис. 9.5).
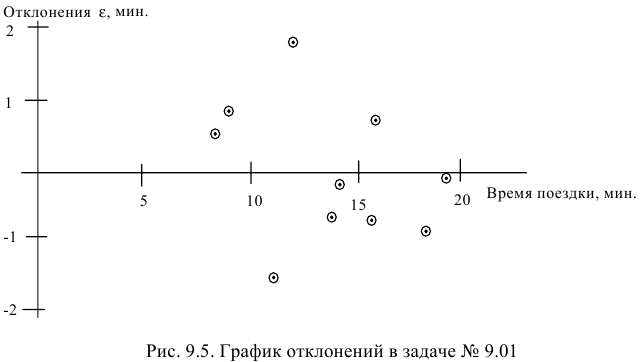
Отложим отклонения 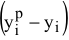 по оси
по оси 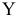 , для каждого значения
, для каждого значения 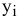 . Если регрессионная модель близка к реальной зависимости, то отклонения будут носить случайный характер и их сумма будет близка к нулю. В рассмотренном примере
. Если регрессионная модель близка к реальной зависимости, то отклонения будут носить случайный характер и их сумма будет близка к нулю. В рассмотренном примере
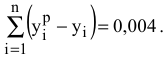
Нелинейная регрессия
Рассмотрим наиболее простые случаи нелинейной регрессии: гиперболу, экспоненту и параболу. При нахождении коэффициентов гиперболы и экспоненты используют прием приведения нелинейной регрессионной зависимости к линейному виду. Это позволяет использовать для вычисления коэффициентов функций регрессии формулы (9.3).
Гипербола
При нахождении гиперболы 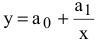 вводят новую переменную
вводят новую переменную 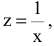 тогда уравнение гиперболы принимает линейный вид
тогда уравнение гиперболы принимает линейный вид 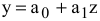 .
.
После этого используют формулы (9.3) для нахождений линейной функции, но вместо значении 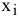 используются значения
используются значения 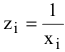
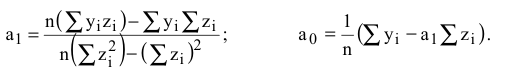
При проведении вычислений во вспомогательную таблицу вносятся соответствующие колонки.
Экспонента
Для приведения к линейному виду экспоненты 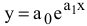 проведем логарифмирование
проведем логарифмирование
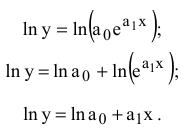
Введем переменные
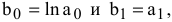
тогда
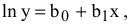
откуда следует, что можно применять формулы (9.3), в которых вместо значений 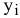 надо использовать
надо использовать 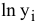
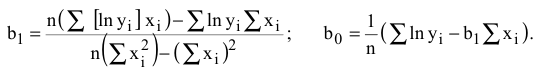
При этом мы получим численные значения коэффициентов 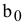 и
и 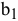 , от которых надо перейти к
, от которых надо перейти к 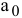 и
и 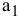 , используемых в модели экспоненты. Исходя из введенных обозначений и определения логарифма, получаем
, используемых в модели экспоненты. Исходя из введенных обозначений и определения логарифма, получаем
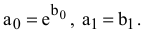
Парабола
Для нахождения коэффициентов параболы
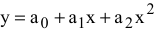
необходимо решить линейную систему из трех уравнений
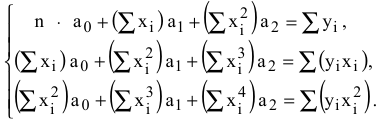
Сила регрессионной связи для гиперболы и параболы определяется непосредственно по формуле (9.2). При вычислении коэффициента детерминации экспоненты все значения параметра 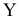 (исходные, регрессионные, среднее) необходимо заменить на их логарифмы, например,
(исходные, регрессионные, среднее) необходимо заменить на их логарифмы, например, 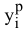 — на
— на 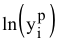 и т.д.
и т.д.
Методы скользящего среднего и экспоненциального сглаживания
Методы скользящего среднего и экспоненциального сглаживания используются для прогнозирования временных рядов. Формально временной ряд — это множество пар данных 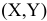 , в которых
, в которых 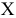 — это моменты или периоды времени (независимая переменная), a
— это моменты или периоды времени (независимая переменная), a 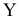 — параметр (зависимая переменная), характеризующий величину исследуемого явления. Цель исследования временных рядов состоит в выявлении тенденции изменения фактических значений параметра
— параметр (зависимая переменная), характеризующий величину исследуемого явления. Цель исследования временных рядов состоит в выявлении тенденции изменения фактических значений параметра 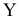 во времени и прогнозировании будущих значений
во времени и прогнозировании будущих значений 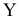 . Модель, построенную по ретроспективным данным можно использовать при наличии устоявшейся тенденции в динамике значений прогнозируемого параметра. К возможным ситуациям нарушения такой тенденции относятся: коренное изменение плана деятельности фирмы, которая стала терпеть убытки; резкое изменение параметров внутренней или внешней ситуации (цен на сырье; уровня инфляции); стихийные бедствия, военные действия, общественные беспорядки.
. Модель, построенную по ретроспективным данным можно использовать при наличии устоявшейся тенденции в динамике значений прогнозируемого параметра. К возможным ситуациям нарушения такой тенденции относятся: коренное изменение плана деятельности фирмы, которая стала терпеть убытки; резкое изменение параметров внутренней или внешней ситуации (цен на сырье; уровня инфляции); стихийные бедствия, военные действия, общественные беспорядки.
Суть методов скользящего среднего и экспоненциального сглаживания состоит в том, фактические уровни исследуемого временного ряда заменяются их средними значениями, погашающими случайные колебания. Это позволяет более четко выделить основную тенденцию изменения исследуемого параметра. Эти относительно простые методы прогнозирования временных рядов, основанные на представлении прогноза 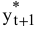 в виде суммы
в виде суммы 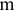 предыдущих наблюдаемых значений
предыдущих наблюдаемых значений 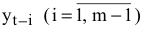 , причем каждое из них учитывается с определенным весовым коэффициентом
, причем каждое из них учитывается с определенным весовым коэффициентом 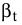
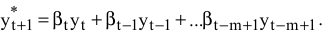
Использование методов скользящего среднего и экспоненциального сглаживания основано на следующих допущениях:
• временной ряд является устойчивым в том смысле, что его элементы являются реализациями следующего случайного процесса:
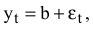
где 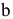 — неизвестный постоянный параметр,
— неизвестный постоянный параметр, 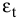 — случайная ошибка.
— случайная ошибка.
• случайная ошибка 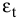 имеет нулевое математическое ожидание и постоянную дисперсию;
имеет нулевое математическое ожидание и постоянную дисперсию;
• данные для различных периодов времени не коррелированны.
Метод скользящего среднего
Расчет прогноза и сглаживание временного ряда методом скользящего среднего производится по формуле
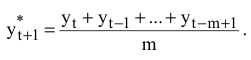
При этом предполагается, что все 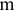 значений
значений 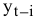 за
за 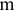 моментов времени вносят равный вклад в прогнозируемое значение
моментов времени вносят равный вклад в прогнозируемое значение 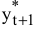 и учитываются с одинаковым весовым коэффициентом
и учитываются с одинаковым весовым коэффициентом 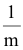 .
.
Метод экспоненциального сглаживания
В методе экспоненциального сглаживания весовые коэффициенты предыдущих наблюдаемых значений увеличиваются по мере приближения к последним (по времени) данным. Кроме того, в формировании прогнозируемого значения участвуют все 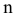 известных значений
известных значений 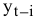
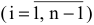 временного ряда
временного ряда
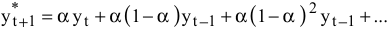
Для расчета прогноза и для сглаживания временного ряда методом экспоненциального сглаживания используют формулу (10.2) в виде
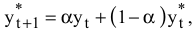
где 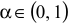 — константа сглаживания. Таким образом, значение
— константа сглаживания. Таким образом, значение 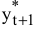 можно вычислить рекуррентно на основании значения
можно вычислить рекуррентно на основании значения 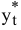 .
.
Задачам 10.01
Постройте и проанализируйте график временного ряда, представленного в табл. 10.1 с точки зрения применимости методов скользящего среднего и экспоненциального сглаживания.
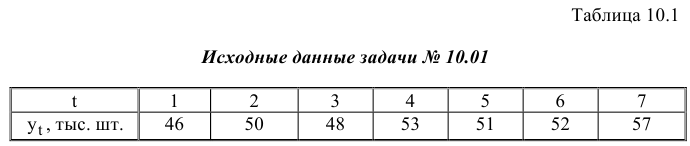
Сделайте прогноз для 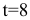 методом скользящей средней для
методом скользящей средней для 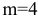 ; методом экспоненциального сглаживания для
; методом экспоненциального сглаживания для 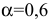 .
.
Решение:
График исходного временного ряда представлен на рис. 10.1.
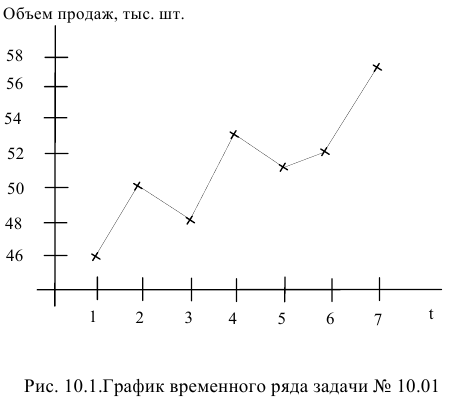
Из графика видно, что наблюдается явная тенденция к возрастанию значений временного ряда 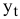 , что приведет к неточности в прогнозах, выполненных методами скользящего среднего и экспоненциального сглаживания (это следует из допущений методов), к подавлению этой тенденции.
, что приведет к неточности в прогнозах, выполненных методами скользящего среднего и экспоненциального сглаживания (это следует из допущений методов), к подавлению этой тенденции.
Для прогнозирования методом скользящего среднего достаточно выполнить единственный расчет
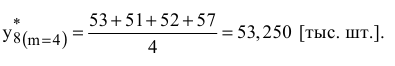
Для прогнозирования методом экспоненциального сглаживания необходимо провести расчеты для всех моментов времени, за исключением  :
:

Не существует четкого правила для выбора числа членов скользящей средней 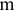 или параметра экспоненциального сглаживания
или параметра экспоненциального сглаживания 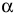 . Они определяются статистикой исследуемого процесса. Чем меньше
. Они определяются статистикой исследуемого процесса. Чем меньше 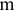 и чем больше
и чем больше 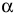 , тем сильнее реагирует прогноз на колебания временного ряда, и наоборот, чем больше
, тем сильнее реагирует прогноз на колебания временного ряда, и наоборот, чем больше 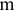 и чем меньше ос, тем более инерционным является процесс прогнозирования. На практике величина
и чем меньше ос, тем более инерционным является процесс прогнозирования. На практике величина 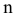 обычно принимается в пределах от 2 до 10, а
обычно принимается в пределах от 2 до 10, а 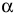 — в пределах от 0,01 до 0,30. При наличии достаточного числа элементов временного ряда значение
— в пределах от 0,01 до 0,30. При наличии достаточного числа элементов временного ряда значение 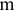 и
и 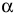 , приемлемое для прогноза, можно определить следующим образом:
, приемлемое для прогноза, можно определить следующим образом:
• задать несколько предварительных значений 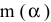 ;
;
• сгладить временной ряд, используя каждое заданное значение 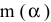 ;
;
• вычислить среднюю ошибку прогнозирования как среднее абсолютное отклонение (mean absolut deviation — MAD)
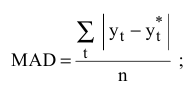
• выбрать значение 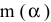 , соответствующее минимальной ошибке.
, соответствующее минимальной ошибке.
Кстати готовые на продажу задачи тут, и там же теория из учебников может быть вам поможет она.
Управление запасами. Основные модели управления запасами
Модель Уилсона
Математические модели управления запасами (УЗ) позволяют найти оптимальный уровень запасов некоторого товара, минимизирующий суммарные затраты на покупку, оформление и доставку заказа, хранение товара, а также убытки от его дефицита. Модель Уилсона является простейшей моделью УЗ и описывает ситуацию закупки продукции у внешнего поставщика, которая характеризуется следующими допущениями:
• интенсивность потребления является априорно известной и постоянной величиной;
• заказ доставляется со склада, на котором хранится ранее произведенный товар;
• время поставки заказа является известной и постоянной величиной;
• каждый заказ поставляется в виде одной партии;
• затраты на осуществление заказа не зависят от размера заказа;
• затраты на хранение запаса пропорциональны его размеру;
• отсутствие запаса (дефицит) является недопустимым.
Входные параметры модели Уилсона
1) 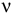 — интенсивность (скорость) потребления запаса, [ед. тов. / ед. t];
— интенсивность (скорость) потребления запаса, [ед. тов. / ед. t];
2) 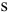 — затраты на хранение запаса, [руб./ед.тов. • ед. t ];
— затраты на хранение запаса, [руб./ед.тов. • ед. t ];
3) 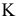 — затраты на осуществление заказа, включающие оформление и доставку заказа, [руб.];
— затраты на осуществление заказа, включающие оформление и доставку заказа, [руб.];
4) 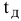 — время доставки заказа, [ед. t ].
— время доставки заказа, [ед. t ].
Выходные параметры модели Уилсона
1) 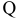 — размер заказа, [ед. тов.];
— размер заказа, [ед. тов.];
2) 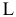 — общие затраты на управление запасами в единицу времени, [руб./ед-t];
— общие затраты на управление запасами в единицу времени, [руб./ед-t];
3) 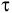 — период поставки, т.е. время между подачами заказа или между поставками, [ед.t];
— период поставки, т.е. время между подачами заказа или между поставками, [ед.t];
4) 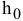 — точка заказа, т.е. размер запаса на складе, при котором надо подавать заказ на доставку очередной партии, [ед. тов.].
— точка заказа, т.е. размер запаса на складе, при котором надо подавать заказ на доставку очередной партии, [ед. тов.].
Циклы изменения уровня запаса в модели Уилсона графически представлены на рис. 11.1. Максимальное количество продукции, которая находится в запасе, совпадает с размером заказа 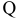 .
.
Уровень запасов
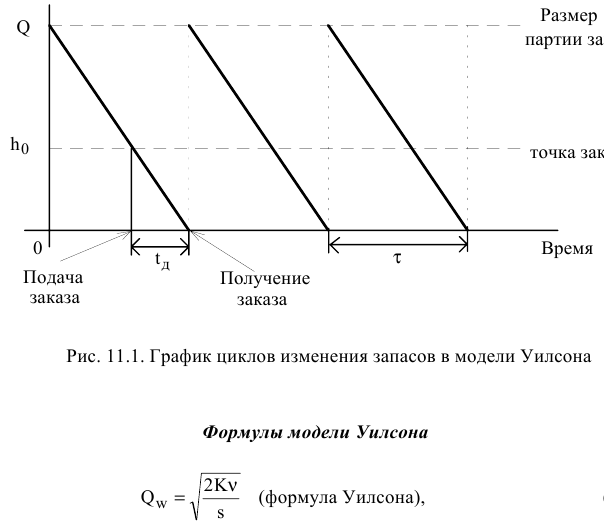
где 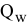 — оптимальный размер заказа в модели Уилсона;
— оптимальный размер заказа в модели Уилсона;
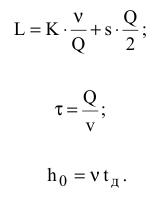
График затрат на УЗ в модели Уилсона представлен на рис. 11.2
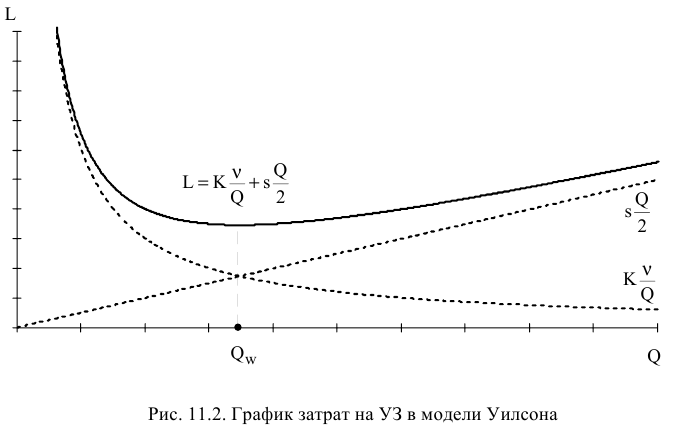
11.1.2. Модель планирования экономичного размера партии
Модель Уилсона, используемую для моделирования процессов закупки продукции у внешнего поставщика, можно модифицировать и применять в случае собственного производства продукции. На рис. 11.3 схематично представлен некоторый производственный процесс. На первом станке производится партия деталей с интенсивностью 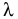 . деталей в единицу времени, которые используются на втором станке с интенсивностью
. деталей в единицу времени, которые используются на втором станке с интенсивностью 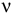 [дет./ед.t].
[дет./ед.t].
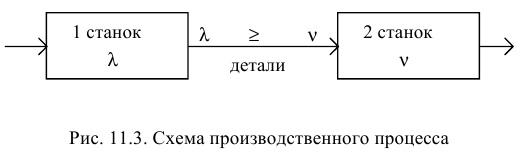
1) 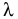 — интенсивность производства продукции первым станком, [ед. тов./ед. t];
— интенсивность производства продукции первым станком, [ед. тов./ед. t];
2) 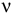 — интенсивность потребления запаса, [ед. тов./ед. t];
— интенсивность потребления запаса, [ед. тов./ед. t];
3) 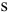 — затраты на хранение запаса, [руб./ед.тов. • ед t ];
— затраты на хранение запаса, [руб./ед.тов. • ед t ];
4) 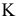 — затраты на осуществление заказа, включающие подготовку (переналадку) первого станка для производства продукции, потребляемой на втором станке, [руб.];
— затраты на осуществление заказа, включающие подготовку (переналадку) первого станка для производства продукции, потребляемой на втором станке, [руб.];
5) 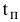 — время подготовки производства (переналадки), [ед t ].
— время подготовки производства (переналадки), [ед t ].
Выходные параметры модели планирования экономичного размера партии
1)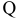 — размер заказа, [ед. тов.];
— размер заказа, [ед. тов.];
2) 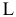 — общие затраты на управление запасами в единицу времени, [руб./ед t ];
— общие затраты на управление запасами в единицу времени, [руб./ед t ];
3) 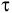 — период запуска в производство партии заказа, т.е. время между включениями в работу первого станка, [ед. t];
— период запуска в производство партии заказа, т.е. время между включениями в работу первого станка, [ед. t];
4) 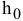 — точка заказа, т.е. размер запаса, при котором надо подавать заказ на производство очередной партии, [ед. тов.].
— точка заказа, т.е. размер запаса, при котором надо подавать заказ на производство очередной партии, [ед. тов.].
Изменение уровня запасов происходит следующим образом (рис. 11.4):
• в течение времени 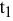 работают оба станка, т.е. продукция производится и потребляется одновременно, вследствие чего запаса накапливается с интенсивностью
работают оба станка, т.е. продукция производится и потребляется одновременно, вследствие чего запаса накапливается с интенсивностью 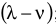 ;
;
• в течение времени 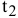 работает только второй станок, потребляя накопившийся запас с интенсивностью
работает только второй станок, потребляя накопившийся запас с интенсивностью 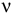 .
.
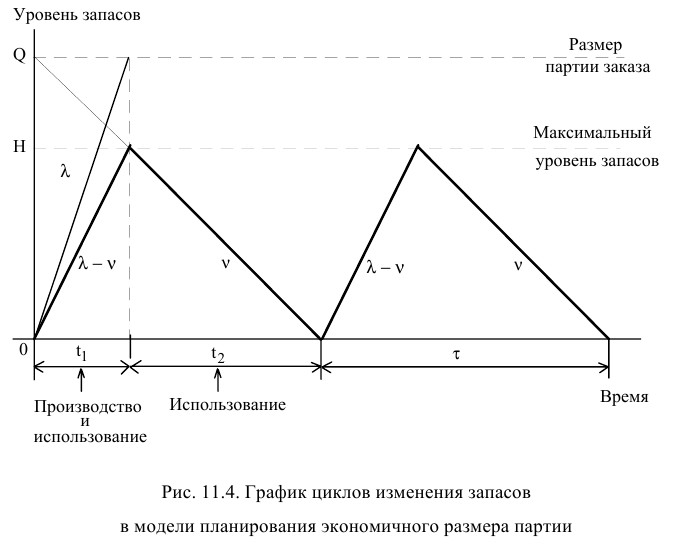
Формулы модели экономичного размера партии
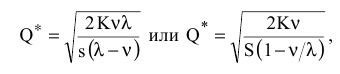
где * — означает оптимальность размера заказа;
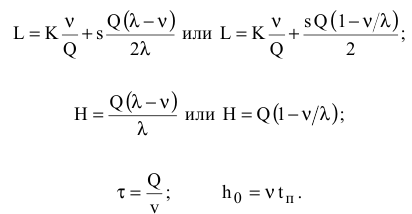
Основная сложность при решении задач по УЗ состоит в правильном определении входных параметров задачи, поскольку не всегда в условии их числовые величины задаются в явном виде. При использовании формул модели УЗ необходимо внимательно следить за тем, чтобы все используемые в формуле числовые величины были согласованы по единицам измерения. Так, например, оба параметра 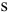 и
и 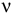 должны быть приведены к одним и тем же временных единицам (к дням, к сменам или к годам), параметры
должны быть приведены к одним и тем же временных единицам (к дням, к сменам или к годам), параметры 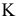 и
и 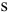 должны измеряться в одних и тех же денежных единицах и т.д.
должны измеряться в одних и тех же денежных единицах и т.д.
Задача № 11.01
Объем продажи некоторого магазина составляет в год 500 упаковок супа в пакетах. Величина спроса равномерно распределяется в течение года. Цена покупки одного пакета равна 2 руб. За доставку заказа владелец магазина должен заплатить 10 руб. Время доставки заказа от поставщика составляет 12 рабочих дней (при 6-дневной рабочей неделе). По оценкам специалистов, издержки хранения в год составляют 40 коп. за один пакет. Необходимо определить: сколько пакетов должен заказывать владелец магазина для одной поставки; частоту заказов; точку заказа. Известно, что магазин работает 300 дней в году.
Решение:
Примем за единицу времени год, тогда 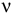 = 500 шт. пакетов в год,
= 500 шт. пакетов в год, 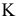 =10 руб.,
=10 руб., 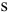 = 0,4 руб./шт.-год. Поскольку пакеты супа заказываются со склада поставщика, а не производятся самостоятельно, то будем использовать модель Уилсона.
= 0,4 руб./шт.-год. Поскольку пакеты супа заказываются со склада поставщика, а не производятся самостоятельно, то будем использовать модель Уилсона.
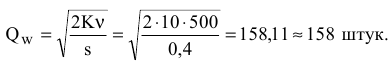
Поскольку число пакетов должно быть целым, то будем заказывать по 158 штук. При расчете других параметров задачи будем использовать не
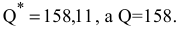
Годовые затраты на УЗ равны
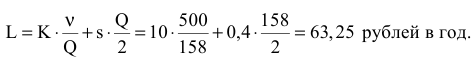
Подачу каждого нового заказа должна производиться через
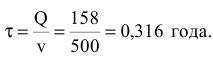
Поскольку известно, что в данном случае год равен 300 рабочим дням, то
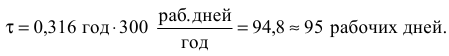
Заказ следует подавать при уровне запаса, равном
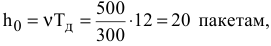
т.е. эти 20 пакетов будут проданы в течение 12 дней, пока будет доставляться заказ.
Задача №11.02
На некотором станке производятся детали в количестве 2000 штук в месяц. Эти детали используются для производства продукции на другом станке с интенсивностью 500 шт. в месяц. По оценкам специалистов компании, издержки хранения составляют 50 коп. в год за одну деталь. Стоимость производства одной детали равна 2,50 руб., а стоимость на подготовку производства составляет 1000 руб. Каким должен быть размер партии деталей, производимой на первом станке, с какой частотой следует запускать производство этих партий?
Решение:
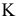 =1000 руб.,
=1000 руб., 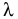 = 2000 шт. в месяц или 24000 шт. в год,
= 2000 шт. в месяц или 24000 шт. в год, 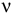 = 500 шт. в месяц или 6000 шт. в год,
= 500 шт. в месяц или 6000 шт. в год, 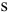 = 0,50 руб. в год за деталь. В данной ситуации необходимо использовать модель планирования экономичного размера партии.
= 0,50 руб. в год за деталь. В данной ситуации необходимо использовать модель планирования экономичного размера партии.

Частота запуска деталей в производство равна
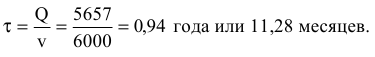
Общие затраты на УЗ составляют
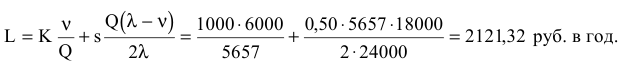
доставки гравия, которые были проанализированы при решении задачи. Покажите на этих графиках оптимальные объемы заказа для каждого из вариантов и окончательно выбранный размер заказа.
Задача № 11.7
В течение смены длительностью 24 дня в санатории отдыхают 83 человека. Ежедневно каждый из отдыхающих должен получить 200 г кефира. Кефир на молокозаводе пакуется в пакеты по 0,5 л (6 руб./шт) и 1 л (10 руб./шт) и доставляется транспортом санатория в течение 2 часов. Срок годности кефира ограничен 5 днями. Его хранение в холодильниках санатория обходится в среднем в 12 коп. за 1 л в сутки. Стоимость оформления и доставки заказа составляет 54 руб.
Организуйте поставку кефира в санаторий в течение одной санаторной смены, учитывая в затратах на УЗ (12.1) цену покупки кефира. Постройте график циклов изменения запаса кефира.
Задачам 11.8*
Придумайте условие задачи УЗ, максимально приближенное к реальности, для которого могут быть использованы описанные модели УЗ (одна из моделей). Решите эту задачу.
Пример ситуации для задачи: семья из трех человек решает, что выгодней — делать запас картофеля на всю зиму или покупать картофель в течение зимы мелкими партиями. При этом надо учесть такие факторы, как потери картофеля при хранении в домашних условиях, возможное повышение цен на картофель в течение рассматриваемого периода и т.д.
Модель управления запасами, учитывающая скидки
Уравнение общих затрат для ситуации, когда учитываются затраты на покупку товара, имеет вид
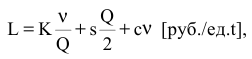
где 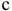 — цена товара [руб./ед. тов.];
— цена товара [руб./ед. тов.]; 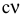 — затраты на покупку товара в единицу времени [руб./ед.t]. Если цена закупки складируемого товара постоянна и не зависит от
— затраты на покупку товара в единицу времени [руб./ед.t]. Если цена закупки складируемого товара постоянна и не зависит от 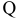 , то ее включение в уравнение общих затрат приводит к перемещению графика этого уравнения параллельно оси
, то ее включение в уравнение общих затрат приводит к перемещению графика этого уравнения параллельно оси  и не изменяет его формы (см. рис. 12.1). Т.е. в случае постоянной цены товара ее учет не меняет оптимального решения
и не изменяет его формы (см. рис. 12.1). Т.е. в случае постоянной цены товара ее учет не меняет оптимального решения 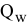 .
.
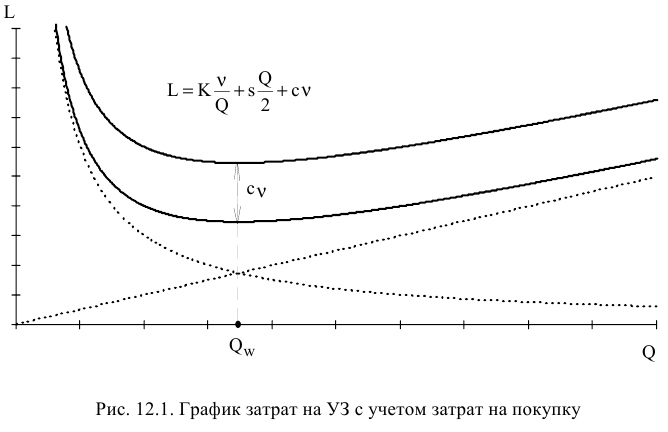
Если на заказы большого объема предоставляются скидки, то заказы на более крупные партии повлекут за собой увеличение затрат на хранение, но это увеличение может быть компенсировано снижением закупочной цены. Таким образом, оптимальный размер заказа может изменяться по сравнению с ситуацией отсутствия скидок.
Поэтому затраты на приобретение товара необходимо учитывать в модели покупок со скидками.
Новые входные параметры модели, учитывающей скидки
1) 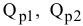 — точки разрыва цен, т.е. размеры покупок, при которых начинают действовать соответственно первая и вторая скидки, [ед. тов.];
— точки разрыва цен, т.е. размеры покупок, при которых начинают действовать соответственно первая и вторая скидки, [ед. тов.];
2) 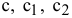 — соответственно исходная цена, цена с первой скидкой, цена со второй скидкой, [руб./ед. тов.].
— соответственно исходная цена, цена с первой скидкой, цена со второй скидкой, [руб./ед. тов.].
Влияние единственной скидки на общие затраты на УЗ показано на рис. 12.2.
Чтобы определить оптимальный размер заказа 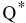 , необходимо проанализировать, в какую из трех областей попадает точка разрыва цены
, необходимо проанализировать, в какую из трех областей попадает точка разрыва цены 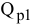 (см. рис. 12.2). Правило выбора
(см. рис. 12.2). Правило выбора 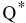 для случая с одной скидкой имеет вид:
для случая с одной скидкой имеет вид:

Правильность решения задач с УЗ со скидками в большой степени определяется качественно построенным графиком общих затрат с указанием на графике всех параметров, используемых при решении. Поэтому в первую очередь необходимо анализировать ситуацию графически и только после этого проводить численные вычисления. Например, если внимательно проанализировать ситуации на рис. 12.2, то можно принимать решение без непосредственного использования правила (12.2). Зрительно легко определить более «выгодный» объем заказа, найдя точку, координата которой по оси 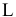 лежит ниже других вариантов заказов.
лежит ниже других вариантов заказов.
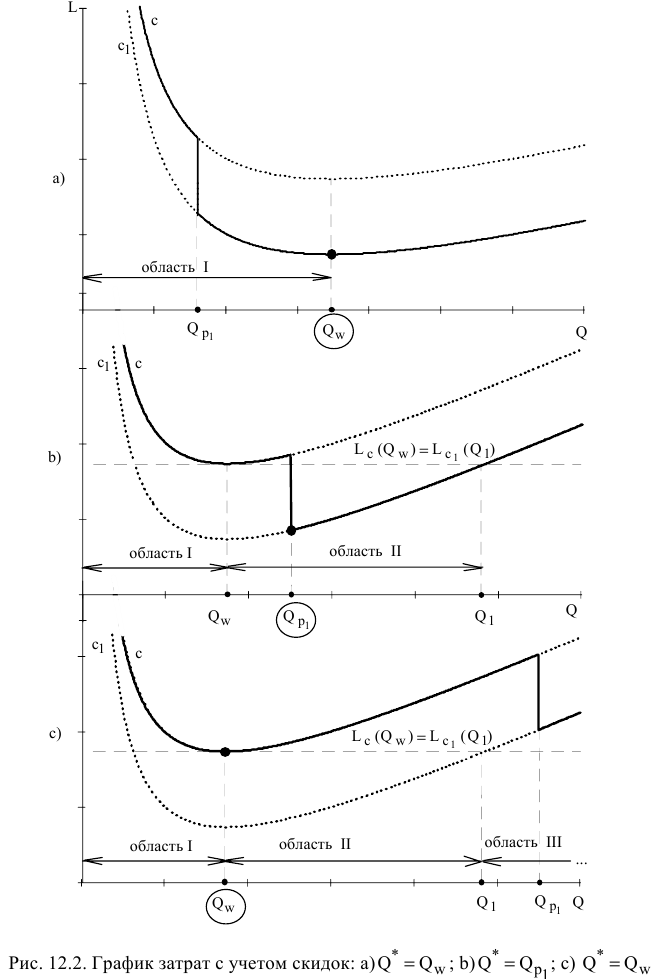
При решении задач с двумя скидками сначала находится оптимальный объем заказа с учетом первой скидки, а затем рассматривается вторая скидка, т.е. обе подзадачи решаются по правилу (12.2).
Задача №12.01
Пусть затраты на заказ равны 10 руб., затраты на хранение продукции
1 руб. в сутки, интенсивность потребления товара 5 шт. в день, цена товара —
2 руб. за штуку, а при объеме закупки 15 шт. и более — 1 руб. Определите оптимальный размер заказа, цену покупки и затраты на УЗ.
Решение:
Начинаем решение с приблизительного построения пунктирными линиями графиков двух функций общих затрат, соответствующих двум ценам, которые указываем над соответствующими линиями затрат: 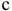 = 2 руб./шт. и
= 2 руб./шт. и 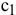 =1 руб./шт. (рис. 12.3).
=1 руб./шт. (рис. 12.3).
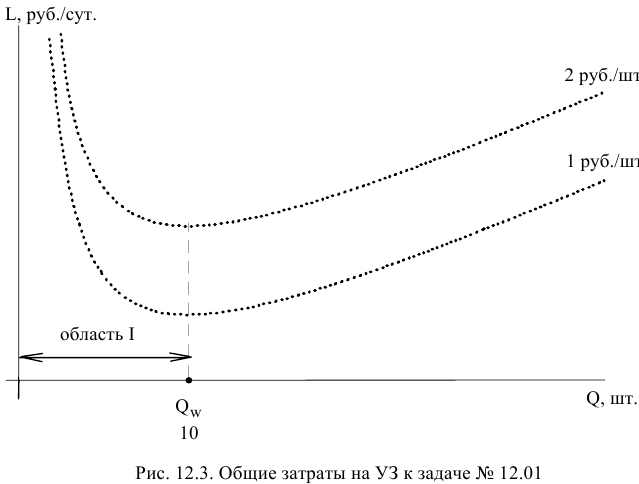
Поскольку объем заказа, задаваемый формулой Уилеона (11.1), легко определяется зрительно как точка минимума обеих функций, то без предварительных вычислений графически находим объем Уилеона 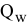 и отмечаем его на графике.
и отмечаем его на графике.
Только после этого, используя параметры 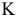 =10 руб.,
=10 руб., 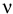 = 5 шт. в день,
= 5 шт. в день,  = 1 руб. за 1 шт. в сутки, вычисляем значение
= 1 руб. за 1 шт. в сутки, вычисляем значение 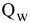 и подписываем его на графике под обозначением
и подписываем его на графике под обозначением 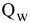 .
.
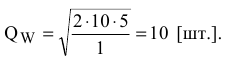
Очевидно, что в область I 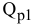 = 15 шт. не попадает, т.к.
= 15 шт. не попадает, т.к. 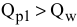 . Таким образом,
. Таким образом, 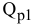 может попасть в области II или III. Границей между этими областями служит размер заказа
может попасть в области II или III. Границей между этими областями служит размер заказа 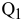 , уравнивающий общие затраты при цене со скидкой 1 руб./шт. и затраты при заказе
, уравнивающий общие затраты при цене со скидкой 1 руб./шт. и затраты при заказе 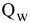 по исходной цене 2 руб./шт. Сначала строим
по исходной цене 2 руб./шт. Сначала строим 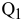 графически (рис. 12.4).
графически (рис. 12.4).
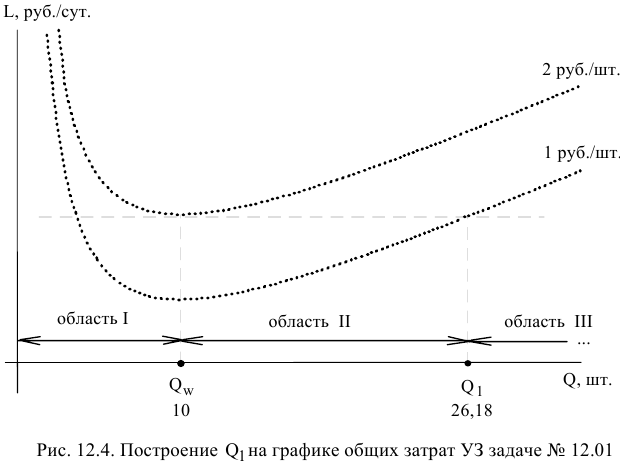
Только после этого найдем 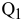 численно. Используя рис. 12.4, запишем выражение, показывающее равенство затрат,
численно. Используя рис. 12.4, запишем выражение, показывающее равенство затрат,
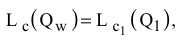
с численными значениями параметров:
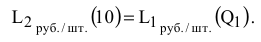
После использования (12.1) для раскрытия левой и правой частей (12.3) получаем
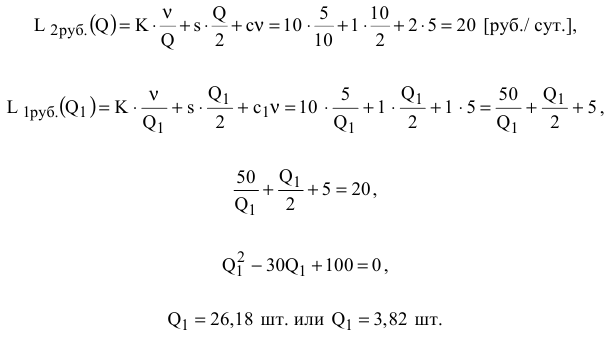
Всегда выбираем больший из корней 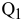 =26,18, т.к. меньший по
=26,18, т.к. меньший по
значению корень не дает нам информации о границе областей II и III (см. рис. 12.4), и отмечаем численное значение 26,18 на графике.
Таким образом, точка разрыва цен 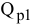 = 15 попадает в область II, т.к.
= 15 попадает в область II, т.к.
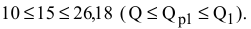
Отметим эту точку на графике в любом месте области II (рис. 12.5).
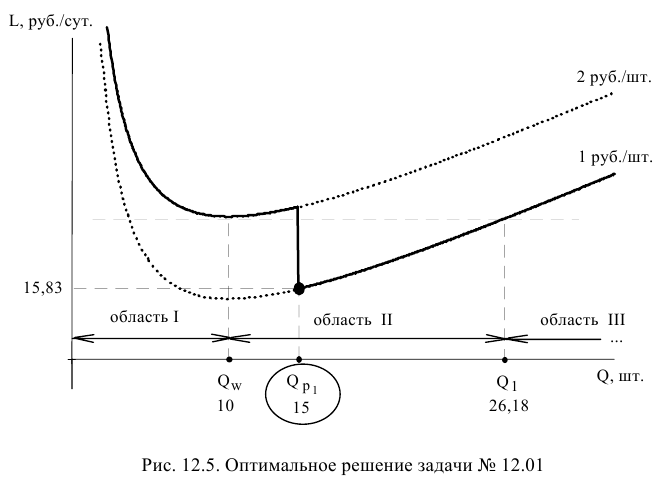
После этого сплошной линией обведем те участки обеих функций затрат, которые соответствуют действующим ценам, т.е. до объема 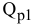 =15 обведем верхнюю линию затрат, а после — нижнюю.
=15 обведем верхнюю линию затрат, а после — нижнюю.
Согласно правилу (12.2) и графику (см. рис. 12.5) оптимальным является объем заказа 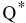 =15 шт. по цене 1 руб./шт. Таким образом, в данной ситуации скидкой пользоваться выгодно. Общие затраты при этом составляют
=15 шт. по цене 1 руб./шт. Таким образом, в данной ситуации скидкой пользоваться выгодно. Общие затраты при этом составляют
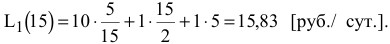
Если бы заказывали по 10 шт. товара, то общие затраты составили бы 20 рублей, т.е. при заказе в 15 шт. экономия средств составляет 4,17 рублей в сутки.
Задача №12.02
Рассмотрим задачу № 11.01. Пусть поставщик супа в пакетах предоставляет следующие скидки
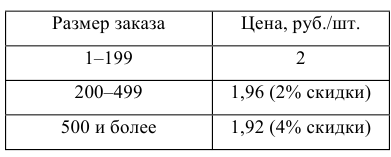
Следует ли владельцу магазина воспользоваться одной из скидок, предоставляемых поставщиком? Каковы при этом будут размер заказа и общие затраты на УЗ?
Решение:
- Строим пунктирными линиями графики трех функций затрат и обозначаем на них соответствующие цены
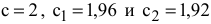 (рис. 12.6). Строим на графике точку, соответствующую
(рис. 12.6). Строим на графике точку, соответствующую  .
.
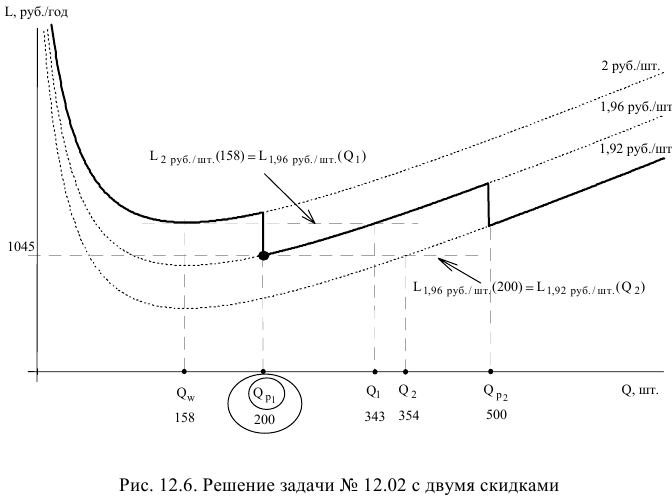
- Вычисляем значение
 = 158 (см. решение задачи № 11.01), отмечаем это значение на графике.
= 158 (см. решение задачи № 11.01), отмечаем это значение на графике.
- Поскольку
 = 200 не попадает в область I, то необходимо найти границу областей II и III. Для этого строим на графике уровень затрат, соответствующий заказу
= 200 не попадает в область I, то необходимо найти границу областей II и III. Для этого строим на графике уровень затрат, соответствующий заказу 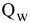 и цене с=2 руб. до пересечения со второй линией затрат, и графически находим и строим
и цене с=2 руб. до пересечения со второй линией затрат, и графически находим и строим 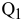 .
.
- Находим
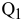 численно, используя выражение
численно, используя выражение
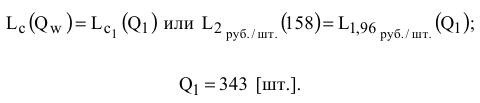
- Используя правило (12.2) и график на рис. 12.6, находим более дешевый объем заказа (с учетом только первой скидки)
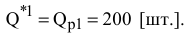
- Чтобы рассмотреть вторую скидку, построим на графике уровень затрат, соответствующий заказу, оптимальному при действии только первой #1 скидки, т.е.
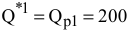 и цене
и цене 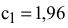 руб./шт. При пересечении этого уровня и третьей линии общих затрат графически определяем
руб./шт. При пересечении этого уровня и третьей линии общих затрат графически определяем 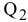 .
.
- Находим численно
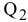 =354, исходя из выражения
=354, исходя из выражения
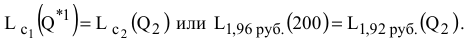
- Используя правило (12.2) и график затрат, находим наиболее дешевый объем заказа с учетом первой и второй скидок
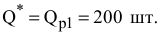
- Таким образом, пользоваться второй скидкой владельцу магазина невыгодно. Оптимальный для него вариант — заказывать 200 пакетов по цене 1,96 руб./шт. обойдется в