Определение метрического пространства. Примеры

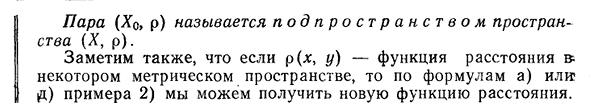
Определение метрического пространства. Примеры

• Определение метрического пространства. Образцы. Мы уже подчеркивали, что понятие пределов играет фундаментальную роль в анализе. В основе этого понятия лежит определение расстояния между числами, то есть абсолютного значения разницы между этими числами. Поэтому представляется естественным ввести понятие расстояния между любыми двумя элементами некоторого

абстрактного множества X, а не между двумя числами. В связи с вышеизложенным приведем следующее определение. О П Р Е Д Е Л Е Н и Е1. 1) p (x, Y)=0, только если x=y;2) p (x, y)=p (y, x) (симметричная аксиома) -, 3) p(x, y)—z’) 2+2£(t-z t11zi-Us l+£Ui-yi)2<1=1l-l1-1<£(x c~z cY+2 (£lx. — Zi|2j1 / 2 (£[z-y(|2),/2(z {- y i)2= 1=1 1=1 ‘ 1=1 1=1 =p2 (x, z)4-2p(x, z) p(z, y)+p2(z, y)=[p(x, z)+p (z, y)] 2.

Таким образом, p (x, y) cp (x, z)+p (z, y), и в этом случае устанавливается неравенство треугольника. В Людмила Фирмаль

приведенном выше, мы суммируем Коши-bunyakovsky неравенство N П£/Х (—З£ £ / /з£ — ух=£afii, где я=я = я<=/ХІ-з,|, Би=\КЦ-МК\, элементом которого является X = (ХІ,… x»), можно ввести и другие признаки расстояния, например, считать, что: Ro (x, y)=-Y; — — -.- «x, Y e X, a)1+p (X. Y)здесь функция p (x, y) введена выше (пример 2);или положим Pi (x, Y)=t Ah|x\ — us\ -, b) 1<537 н Pa (JC «f/)=2lx’ ~y l’b) i = l RZ (x>Y) равно 1, Ноль., для x-y\g, для x-y\y) p (x, y) p (x,»/)<1,1 p (x, y)>1, d) Где функция.P (X, Y) определяется, как описано выше. Естественно, что в этом случае одно и то же множество X превращается в другое метрическое

пространство(X, RG).£-0, 1, 2, 3, 4. 3) Пусть Y-множество непрерывных функций, заданных отрезку [a,&]. Введем метрику, которая предполагает P (x, y)==max/x ( / ) — y (t). Результирующее пространство является метрическим пространством. Он представлен C[a,&]=(Y, p). Аналогично, если задать непрерывную дифференцируемую функцию отрезка[a,&], n>1 в Z n раз, то правило P (x>Y)=t a x I * (,) (0-Y{1) (0 1″где x ( £ ) = = x (/), y (^) =y (/). Это пространство обычно обозначается как SP[a, b]=(Z, p), n>1. Пробел C[a, 6] может быть обозначен символом C0[a, B]. 4) V-множество всех ограниченных последовательностей x=(xi,…И

• HP…) Действительное число. Предположим, что эффективность P (x>Y} — sup|x<: — Us I * axiom 1) -3 в метрическом пространстве очевидна. Это пространство обозначается через t=(V, p). Примечание-обратите внимание, что все подмножества метрического пространства (X, p),

XO, являются метрическими пространствами с той же функцией расстояния R. Итак, все подмножества EP являются функциями p (x, g/)=|xt—Y;12) ‘/2•аналогично, I=i любое подмножество C»[a, 6]является метрическим пространством, где n= = 0,1,2,….538 Канал 12. Функции некоторых переменных Пара(x, p)

называется парой пространств (X, p). Также обратите внимание, что если p (x, y) является функцией Людмила Фирмаль

расстояния в некотором метрическом пространстве, вы можете получить новую функцию расстояния по уравнению a) или d (в Примере 2).

Смотрите также:

Математический анализ 1 курс

Предел функции m переменных	Определение метрического пространства.
Бесконечно малые функции m переменных	Понятие непрерывности функции m переменных