Частные производные функции нескольких переменных

Частные производные функции нескольких переменных

• Частные производные функций некоторых переменных. Пусть M (xi, x2,…, XT) — внутренняя точка области назначения функции » =f (xi, x2…..HT дана фиксированная точка M (xi, x2…..XT) отношение частичных приращений(см. пункты 1, 3 и выражения(12.8)и (12.9)) к

соответствующему приращению Axk аргумента x&: x k». . . H~^Xfc,^4-1>>f(X i, Xg,. . . . ХТ)/. I g\DX^ \x k Отношение (12.12) является функцией Axh, определенной для всех ненулевых значений DX&, и точек

L1(x1, x2,…, Xfe-i, Xk+Axk, XL+1,…. X) принадлежит области назначения Людмила Фирмаль

функций u=f (Xi,x2,■■■, XT). Частичное приращение функции в точке M (Xi, x2,) при наличии ограничения на отношение AX ku(12.12)…Для соответствующего приращения Axh аргумента XH в DX^O этот предел устанавливается аргументом xk на часть функции o d nth в точке M

и=~f (x i,x2, XT). И так оно и есть., ——- lim — (12.13)dxk————- DHA-функция в частных производных M=f(xb x2,…(X, xm)по аргументу XY. Одна переменная является нормальной производной функции XY. Фиксированные значения для других переменных. Таким образом, вычисление частной производной осуществляется по обычным правилам вычисления производной функции от некоторой

• переменной. 2: 14-xV PI (1) I = arctg (xy2), U2di DX1 — \ — xgu* ‘ du Hg+ug2) I-e*, — = D — — — — e g, Z Ди Доу. 2У di dz e g x2+U2e XG+g YG z # =0. З а м е ч а н и Е1. Из наличия функции в заданной точке всех подфункций не следует, в общих чертах, НЭП-470Ч. 12. Функции некоторых переменных Неловкость функции в этот момент. Мы уже подтвердили, что функция? (12.10)) «a» P ri % 2+U2 * °> U=x2+Y2

0×2+Y2=O не является смежным при 0(0, 0) (см. Пример D, пункт 2§3).. Это потому, что f (x, 0)=0, f (0, y)=0: =0, L_ / = o. d x (0,0) du|(o, o) З а м е ч а н и Е2. Можно сказать, что определение понятия частных производных всегда подходит для внутренней точки области функции, но для граничной точки этой области вообще не подходит. Это особенно причина. С тем, что»Y»

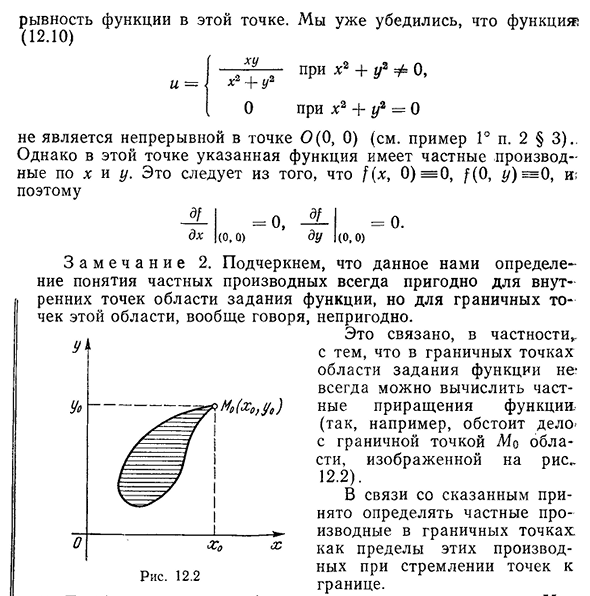
не является граничной точкой области назначения функции- Рис. pri-Pro- Всегда можно вычислить Людмила Фирмаль

частичные приращения функции (например, в случае «граничной точки» области, показанной на рис. 12.2). В связи с вышеизложенным необходимо определить частные производные в граничных точках как пределы этих производных, когда точка направлена на границу

Смотрите также:

Математический анализ 1 курс

Объем тела.	Метод «вилки»
Некоторые классы кубируемых тел.	Метод итераций