Площадь криволинейной трапеции и криволинейного сектора

Площадь криволинейной трапеции и криволинейного сектора

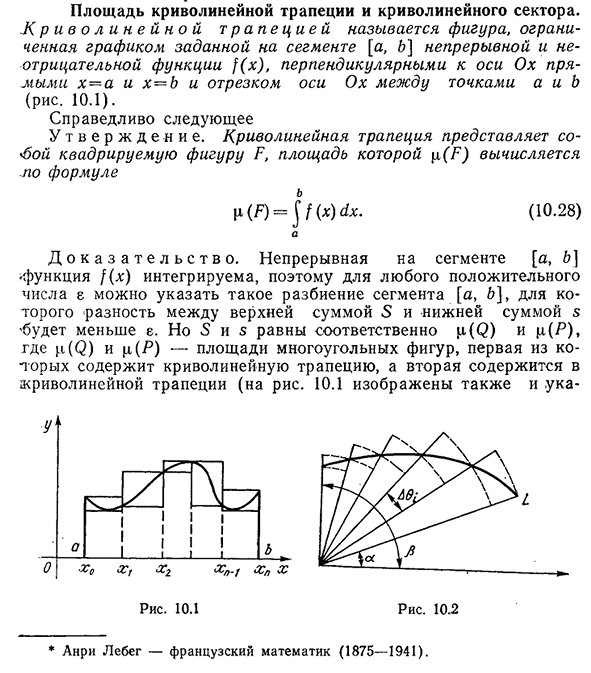
• Площадь криволинейной трапеции и криволинейного сектора. .К р и в О Л и н е й Н О Й Т Р Е С и называется графом, ограниченным графом, заданным в отрезке [a,B]непрерывным и неотрицательным 10.1). Ниже приведен истинный U t V e R W d E n I e. криволинейная

трапеция является Ковариантной фигурой F, в которой площадь p (F) вычисляется по формуле b p (F)=J f (x) dx. (10.28)) Но D o K a z a t e l s T V o. непрерывная функция f (x) [a,^на отрезке интегрируема,

поэтому для любого положительного числа e разность между суммой S выше и суммой s ниже меньше, чем E [A, B]отрезка 10.1 uka также Людмила Фирмаль

обращается- Анри Лебег-французский математик (1875-1941).§2. Плоская фигура площадь 415- Над формой многоугольника). Итак, p (Q) равно C(P)<8,и благодаря теореме 10.2 трапеция кривой квадратична. Для любой интегральной функции пределом, когда

диаметр распределения становится равным нулю, является верхний S и Нижний S S. Если сумма s равна^f (x) dx и s<[x (F) Но Д О К а з а т е л ь с т в о. рассмотрим разбиение отрезков[a,. P] точка a=0o<0i<…Для <0n=p и каждого частичного сегмента{0(-1,0,], построить круговой сектор, радиус которого равен минимальному R и максимальному Rt значению функции R (0) для сегмента[0 (_, 0,). В результате

• получаются две квадриплегические фигуры, первая фигура а входит в изогнутый сектор, а вторая в содержит этот сектор (см. Рисунок). 10.2). Уголок|Т(L)и П(С) при этом парализованный цифр а н н б равна РФ (6?- fy-i) и i=.- i i i=i416 Глава 10. Геометрические приложения

определенных интегралов Первая из этих сумм является малой суммой s, вторая-функцией отрезка[CC, p]указанного разбиения этого отрезка-I-r2(6) на[a, p]функция-^-G2(6)интегрируема в этом отрезке, поэтому разность S-s=(B)-C (A)меньше для любого e>0.

есть небольшое отделение. Так как A и B — два квадратичных числа, то первое из них Людмила Фирмаль

содержится в криволинейном секторе F,а второе, благодаря теореме, содержит F, то число кривой ‘10.2’. Справедливость области (10.29) этого уравнения состоит в том, что эта область p (F) заключена между s=p (A) и S=n (B), и как сумма s, так и S имеют тенденцию быть интегралами справа от (10.29).

Смотрите также:

Математический анализ 1 курс

Площадь плоской фигуры	Примеры вычисления площадей.
Повторные пределы	Случай функции двух переменных