Оглавление:







Классы интегрируемых функций
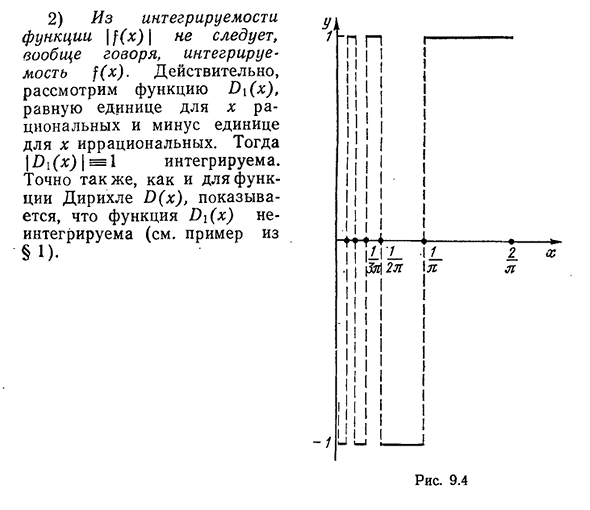
- Класс интегрируемых функций. В Главе 1 этой главы функция f (x) константа сегмента[a,B]интегрируется Риманом в этом сегменте, и этот сегмент интегрируется в этом сегменте, естественно, вызывает вопросы о классе функций, интегрируемых Леманом в сегменте[a, b].
Среди этих классов важную роль играет класс непрерывных функций отрезка[a, b]. Были доказаны следующие основные теоремы. 9.1. Непрерывная функция отрезка[a, b]интегрируется в этом отрезке Риманом. Д О К а з а т е л ь с Т В О. пусть F (x)
непрерывна на отрезке fa, b). Выберем любое число e>0. Поскольку функция f(x)непрерывна Людмила Фирмаль
на отрезке, она равномерно непрерывна, поэтому для заданного e>0 разность между точным дном и вершиной J(x) на любом заданном отрезке, имеющем длину меньше любой B из G’и g’is|g’—g»|0 покрывает все точки останова в этой функции, и если вы можете указать конечное число интервалов с суммой длин меньше e, то функция будет вызвана. Д О К а з а т е л ь с т в о. сделайте M и PG
точными вершиной и дном отрезка [a,&]функции f (x). Заметим, что для M=PG, то есть если функция f (x) является константой, она интегрируема, как уже доказано 1. Поэтому мы предполагаем, что M>PG. Пусть e>0-любое число. Рассмотрим точку останова функции f(x) с конечным числом интервалов, сумма длин которых не превышает числа ei=e/2-(M—PG). Точки отрезков[a, B], не
- принадлежащих заданному интервалу, явно образуют множество, состоящее из конечного числа разделенных отрезков. Добавьте эти сегменты под названием. В каждом из этих сегментов функции непрерывны и поэтому равномерно непрерывны. Итак, если существует такое число b / >0, а 1g-I<0-любое число. Выберите раздел{XA}в сегменте [a,B]диаметра df(a). Оценить разницу ы-ы=£(МК-МК) колледжа,. . k=1 Mk и mk-это верхняя и нижняя
поверхности f (x) на xk-i, xD. Н С-З<е^(ф&—(б)—ф (А)), но не убывающей функцией Фе=п£(МК-МК) = Ф(б) — ф(а). Итак, S-s(xi) — 0,например t^{m, Al]. Кроме того, давайте выберем 6, например 6, в зависимости от интегрируемости функции f(x)функции [a,&].существует раздел{HK}, подобный сегменту [a, B]s-s<82. МК-с SUP Ф(Х), МК = документ INF Ф(Х), Х^ХК-VX и М * K=вечерять ч(х,ТНК=документ INF н(х). X и лексмарк-л-ХК^Х<^Х К-Р xlJ Разделим целое число 1,…N, в двух множествах
A и B: если число k<=a Mk-mft<6, если число p^B Mr-Tr^&. Таким образом, для Людмила Фирмаль
равномерной непрерывности функции<p (f) на отрезке[t, M], если индекс k^A, Mk-mk<8, Mk—m/i^ei получается. Фактически, если принять во внимание индекс/g<=A, то получим Mk-mk= = sup f (x) — inf/(x)<6. [Xk-lXk l XJ-r Xkl т. е. x, y^[xk-i, Xk]разность f (x)-f(y)=(i~h по абсолютной величине не превышает 6:/L-1%\<6, где fi=f(x), t2=f(y). Следовательно, из-за равномерной непрерывности функции<p для всего отрезка[t, M]、 |f (I)— — f (I g/) I= / f (M~f (^)] <6 1. Поскольку последнее неравенство справедливо для любых x и y, принадлежащих отрезку[x — i, x], sup f (/(x)— — inf f (/(^)) —TK^2C ясно, что axk+. k=l k&A +£(M * k-tnk)Axk<e2 (b-a)4-2C£Axft. k £ B eb346 Глава 9. Очистить Интеграл Римана Остается оценить стоимость£DHI. Там есть лев.
Смотрите также:
| Инвариантность формы первого дифференциала | Краевой экстремум |
| Применение дифференциала для установления приближенных формул. | Производные тригонометрических функций |

