Оглавление:


Третье достаточное условие перегиба
- В-третьих, достаточно условий для песни. Мы устанавливаем достаточные условия перегиба, подходящие для случая, когда и вторая, и третья производные функций задачи исчезают в данной
точке C. Аналогом теоремы 7.3 является следующее предложение: Это 7.10. Пусть N^H-четное число, а функция y-f(x) имеет производную
от n в окрестности точки C и производную от n-|-1 в самой точке c. Людмила Фирмаль
Затем, если отношения выполнены =p) (C)=: () <(uz) То есть граф функции y=f (x) имеет изгибы в m (C, f (c)). Д О К а з а т е л ь с Т В О. если I=2, то теорема 7.10 совпадает с уже доказанной теоремой 7.9, поэтому доказательство должно быть сделано только в случае n^4.
Пусть четное число n удовлетворяет условию n>4. F (n+1) (c)=/=O тогда, согласно теореме 6.1, функция fвозрастает в точке B1 (f (n+1) (c)<0) или в этой точке (f0). Кроме того, f(x) в окрестности точки C. В соответствии с формулой Тейлора запишите остаточный член в виде Лагранжа (см. Главы 7 и 8, 6). Мы получаем его для всех x из
- достаточно малой окрестности точек C между x и C. /(2) (х)=/(2)(С)(Х-с)+. . . +— Я — — — — — — — (х-с)н_3 4- (с-3) 1В’ ф{Н)(Г) (с-2)! (х-С^-2.§4. Асимптота графа функций 279 Благодаря соотношению (7.3), записанное разложение принимает вид H2) (x)=(1SH_(X-C) p-2. (7.4)) (ГА-2)!
Поскольку он находится между X и C, то для всех x в окрестности значения f (n) (g) достаточно мал, и поэтому для всей правой части четности p и (7.4*), для теоремы 7.8 C, граф функции y-f (x) » имеет нечетную кривизну в точке m(c, f(C)). Теорема доказана.
З а м е ч а н и Е. Большое значение имеет требование четности теоремы 7.10 n Людмила Фирмаль
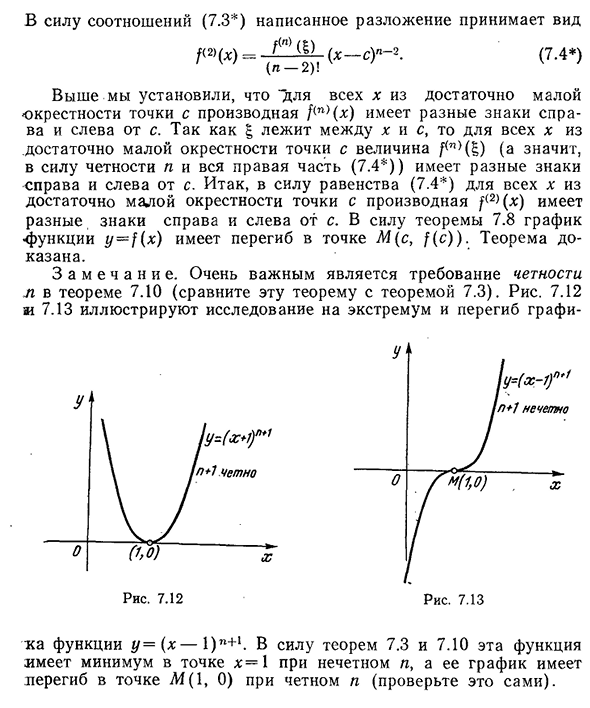
(сравните эту теорему 7.3). Объясните исследование экстремумов и перегибов на рис. 7. 12м7. 13graphi Функция y=(x—l) N+1 ka. Благодаря теоремам 7.3 и 7.10 эта функция имеет минимальное значение при x=1 в нечетном n, а ее график имеет перегиб при m (1,0) в четном n (проверьте сами).
Смотрите также:

