Оглавление:


Отыскание стационарных точек
- Найдите неподвижную точку. Напомним определение локального максимума и локального минимума функции. Для каждой точки в этой окрестности функция оценивает, что значение f (c) является
самым большим (или, соответственно, самым маленьким) из всех значений в f (x) этой функции. Найти стационарную точку 263 Локальные максимальные и
локальные минимальные значения Людмила Фирмаль
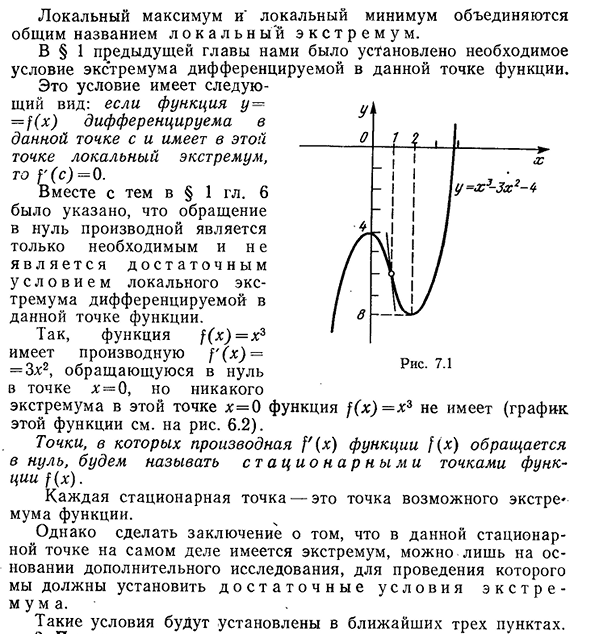
объединены общим названием l o K a l n y E K s t R e M u m. В§1 предыдущей главы мы установили необходимые условия для экстремумов дифференцируемых функций в данной точке. Если
функция y — =f(x)дифференцируема в данной точке C и имеет локальные минимумы в этой точке, то f'(c)=0. Однако в Главе 1, главе 6, необходимо только инвертировать производную и локальные
- экстремумы дифференцируемой функции в данной точке L Oh n s m u s l O V I E m. Итак, функция f(x)=x3 имеет производную f'(x)=3×2, которая исчезает в точке x=0, но функция f(x) = x3 не имеет
экстремального значения в этой точке x=0 (gagrain 6.2) этой функции на рисунке. Точка, в которой фиксируется дифференциал функции fixed), будет называться точкой C t A C и o n A R n s m и функцией f (x). Каждая неподвижная точка является точкой возможной дополнительной функции «Мума».
Однако сделать вывод о том,что в Людмила Фирмаль
данной стационарной точке действительно существует экстремальное значение,можно только на основе дополнительных исследований, для которых мы имеем д О С т о н н т. Такие условия устанавливаются в следующих трех пунктах:
Смотрите также:

