Оглавление:



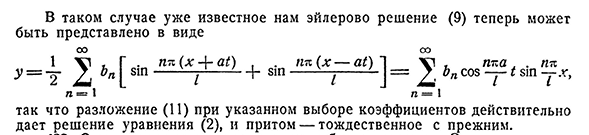

Решение Тейлора и Д. Бернулли
- Тейлор и Д. Бернулли) решение. Еще в 1713 году Тейлор изучил проблему движения натянутых струн и определил период их колебаний. Его отправной точкой было предложение, эквивалентное уравнению(2). В результате он пришел к выводу, что если струна колеблется как единое целое, то она имеет форму синусоидальной
дуги. * ) Даниэль б е р н У Л и (1700-1782), сын Иоганна Бернулли и друг масленка. С 1725 по 1733 год он активно работал в Санкт-Петербургской Академии наук. Конечно, это только одна из возможных строк для типа вариации. Из рассуждений Тейлора следует существование бесчисленного множества таких видов:
нужно только разделить струну на N (2E2) равных участков, каждый из Людмила Фирмаль
которых отдельно применяет предыдущий вывод, в этом случае форма струны представляет собой ряд смежных синусоидальных дуг. Все эти h a S t n s e R e s E n I S уравнения (2) получены чисто аналитическим способом и выведены непосредственно из уравнений. Будем искать это решение (о т л и ч н о е из очевидного^, но для нас оно не интересно-н ы л и), но мы можем видеть отличие от х.
Уравнение(2)в этом случае имеет вид HT » =a2x’t(где штрих означает производную, зависящую от этой переменной) или, наконец,, Один из них、- Оттуда функции (10) Левая часть этого уравнения не зависит от x, а правая I, их суммарное значение на самом деле не зависит от x или I, поэтому принимают вид-a2x2 (X>0) константы и затем формулу (10 «распад на два: T» +D2X2T=O, X » + H2X=0;428 глава XXIV. ряд
- Фурье[421 Эти общие решения уже являются обыкновенными дифференциальными уравнениями, каждое из которых имеет вид: G=Asoz Ah I — \ — IN81P a \ I, X=C C o Z1x — \ — O81p\X. Для функции y=.X T также удовлетворяет ограничивающему условию(3), они должны удовлетворять функции X. предполагая x=0, мы сразу видим, что C=0; предположим x=/: л__л__2К. __72ts Л1-у, Л2—Т’-> Предполагая ноль, это B=0, потому что T'(0)=0, n A h A l L n y e s K o R o s все точки строки t
равны. Обозначим константу AO через NP с X=CP, придем к приведенному выше уравнению последовательности h C t n s x R e W E n и y (2): — pKa. ПК=ИС поп-Я * У Х 81P. Если строка верна, то все строки одинаковы. Вибрируйте с такой же вибрацией такими точками Это соответствует тону определенной высоты. Амплитуда колебаний каждой точки зависит от ее положения и、 … ПК я EP81P-Х. Рисунок 83: вся C-T-руна разделена на n равных участков,все точки в одном участке находятся в одной фазе, а последовательные положения струн в точечном случае l=1, 2, 3, 4 соседних участков показаны на рисунке. 83 точка, в которой одна секция отделяется от
другой, неподвижна.Средняя секция-«пучность» — колеблется с наибольшей Людмила Фирмаль
амплитудой. После появления общих исследований колебаний струн Дальберта и Эйлера Д. Бернулли (1753) провел исследование на ту же тему. Напомнив, что Тейлор еще не распознал многие типы струнных колебаний, Бернулли-основываясь на физических наблюдениях-сказал, что все эти колебания являются»смешанными»(мы бы сказали наложение отдельных вибраций) в его выражении, выполненном в то время, и полные колебания струн могут характеризоваться равенством. Ноль ноль Р=1 Я буду хлопать 81±p-ka. ПП-ч — (я) Если
принять постоянное значение (10) отношения в виде a2x2, то только функция X, равная нулю, может удовлетворять ограничению.421]§5. Очерк по истории тригонометрических функций серии 429 О N о N определяется первым компонентом^, он ответит 2/ Длительность G1= — оставшийся тон, испускаемый струной, или o b E R t o n s, характеризуется другими компонентами; длительность G2=~7}, G3=~ — по G1.. Если вы дотронетесь пальцем до середины струны, то и основной тон, и странные обертоны, с которыми произошла
пучность, сразу исчезнут. Для них вторые обертоны играют роль главных, а струны испускают о в т-а в исходном тоне. Обилие физического содержания, которое идеально соответствовало эксперименту, заключалось в том, что Бернулли предпочитал решение Эйлера (11) решению (9). Надо сказать, что сам Эйлер упоминает решение (11), но только как возможное конкретное решение. Для Бернулли в то время, по его собственному признанию, проблема общности его решения была еще недостаточно ясна, но он понимал, что существуют и другие решения. Теперь мы докажем, опираясь на теорию, разработанную выше, что-п р и Н А Д Л Е Ф А С Е М в Б О Р Е К О Ф И К и Е Н Т О В в формуле (11)*) — следовательно,
предполагается, что мы выполнили те условия относительно ранее наложенного на него курса/(x) [n°419, * ) Проблема коэффициента Бернулли не затрагивается. Начнем с подбора коэффициентов NP. Если вы хотите дать решение, в котором выражение (11) удовлетворяет начальному условию (4): y (x, 0)=/(x) (0x</), предполагая (11) 2=0、 ООО ^&»8Вт Г Х=/(Х) (Ogsl-е^/). (12) Один. Поскольку функция/(x) дифференцируема и исчезает в конце интервала[0,/], возьмем[n°405, (см. 22)] Я /(х)и Н А х(п=1,2,3,…), И это мы предполагаем. Однако ряд (12) сходится к C e x значению x, и функция может быть определена во всем интервале от—OO до 4~OO ОО/х1v * П К Х ч (х)=-
%2* » 8 1П — • Р=1 Таким образом, на интервале[0,/] эта функция будет-^-/(x);а также условие (7) и (8) будет держать его, так как его легче проверить напрямую. Из этого следует, что она точно соответствует функции<p, которая обсуждалась в предыдущем выпуске.430ЧАП. XXIV. ряд Фурье[422 Я В этом случае уже известное решение Эйлера(9) можно представить в виде ОО И 1х1, г*пп(х+А1),. п п (х-А1) 1В пка. PP u=u2 6 4 81P-G+81P — — — — 2EP S05-1 8|P t x’P-1 N=1 расширение (ы) при выборе указанного коэффициента фактически дает решение уравнения (2) и даже совпадает с первым.
Смотрите также:
Решение задач по математическому анализу
| Задача о колебании струны | Спор по поводу задачи о колебании струны |
| Решение Даламбера и Эйлера. | Разложение функций в тригонометрические ряды, определение коэффициентов |

