Оглавление:




Определение разрушающих нагрузок при изгибе балок за пределом упругости
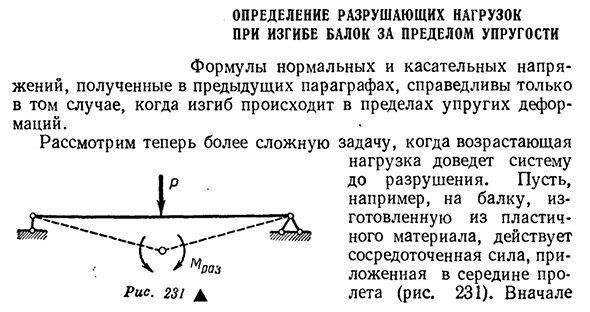
- Определение разрушающей нагрузки При изгибе балок за пределом упругости Уравнения касательных и тангенциальных напряжений, полученные в предыдущем разделе, эффективны только при изгибе в упругой деформации. Давайте теперь рассмотрим более сложные вопросы, когда увеличение Рис, 231D. Нагрузка разрушает систему. Например, на балку, изготовленную из пластического материала,
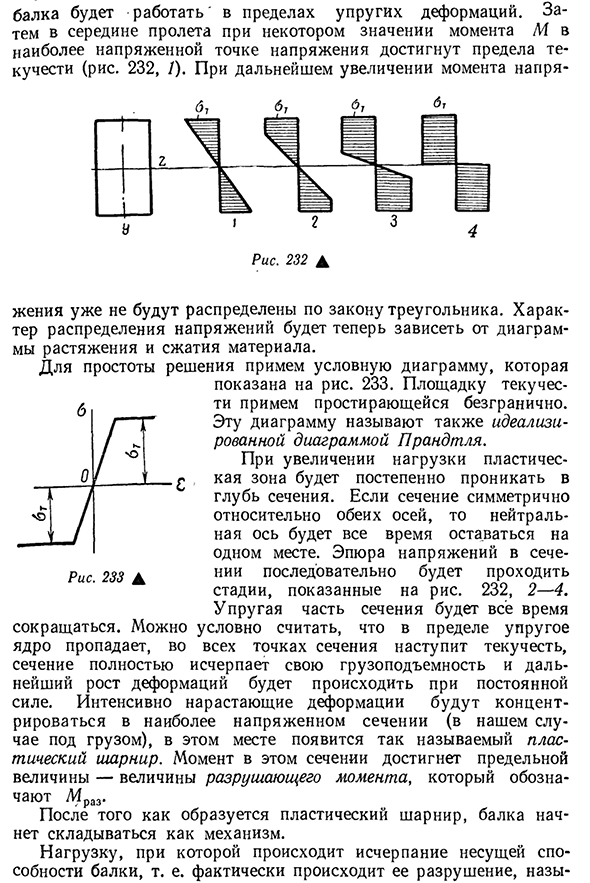
влияет концентрация, соединяющая центр пролета (рис. 231). Первый 258º » работает в пределах упругой деформации. А в середине пролета определенное значение момента M, в наиболее напряженной точке напряжения, достигает предела текучести (рис. 232,/). С дальнейшим увеличением крутящего момента напряжения-
Распределение перестает быть распределенным по законам треугольника. Характер Людмила Фирмаль
распределения напряжений зависит от схемы растяжения и упрощения Рис 233D Сжатие материалов. Давайте посмотрим на условный рисунок, который показан на рисунке. 233 давайте посмотрим на область ликвидности, которая простирается бесконечно. Эта фигура также называется идеализированной диаграммой Прандтля. При увеличении нагрузки пластическая зона будет постепенно проникать в глубину сечения. Если поперечное
сечение симметрично относительно обеих осей, нейтральная ось всегда остается в одном месте. График напряжений в разрезе непрерывно проходит через этапы, показанные на рисунке. 232,2-4. Упругая часть сечения является все время условной и текучей в пределе упругости всех точек сечения, а постоянная расстояния становится концентрической.- Когда уменьшающийся сердечник исчезает, поперечное сечение полностью истощает свою несущую способность, и под действием силы происходит наибольший рост деформации. Интенсивно нарастающая деформация может
- регистрироваться в сильнейшем сечении (под нагрузкой), и в этом месте возникает так называемый пластический шарнир. Момент в этом разделе достигает предельного значения, которое является значением Мраз и заданным разрушающим моментом. Как только пластиковый шарнир сформирован, луч начинает складываться как механизм. Несущая способность балки исчерпывается, то есть нагрузка, при которой ее разрушение фактически происходит、- Девять.* 259вают разрушительную нагрузку. Рассчитать такую
нагрузку несложно. Поэтому будет описан случай, показанный на рисунке. 231 Мраз должен быть приравнен к изгибающему моменту, который вызван силой Р, в то время как предельный момент, возникающий в пластмассовом шарнире, а именно: Для риса. 231 показан момент L4raz, действующий от шарнира на соседнее звено балки. Ниже будет показано, как рассчитать L4raz. Рис 234А Смогите быть установлено от Поперечных размеров и предела текучести материала. Если сечение имеет только одну ось симметрии, соответствующую плоскости нагрузки(рис. 234), сначала возникает проблема определения положения нейтральной оси.
В этом случае нейтральная ось не совпадает с центроидом разделе. В процессе Людмила Фирмаль
деформации нейтральная ось постепенно удаляется от центра тяжести, а в предельном состоянии она принимает условие, что нормальная изгибающая сила равна нулю.Н=ск(1П-а^УГ=0. Э Э Э СИДЖЕЙ РАН После сокращения от получения И » Г-Е-Е СИДЖЕЙ РАН Или СЖ * ‘Р А с Таким образом, нейтральная ось делит сечение. Площадь зоны сжатия равна площади зоны расширения. Если в разрезе есть две оси симметрии, соответствует ли нейтральная ось оси y участка, который не симметричен относительно оси y? Расстояние между осью gg и ней должно определяться из условий уравнения (а). Для каждого конкретного раздела эта задача решается индивидуально. Теперь значение деструктивного момента
260найдем: Здесь-статический момент части сжатия сечения на нейтральной оси г^г, Пять. Рай. — По модулю статического момента растягиваемой детали относительно той же оси, взятой. Покажите =5G+5GT. (8.30) Назовем это значение моментом сопротивления участка в момент разрушения. А разрушительный момент определяется равенством — ^Р а з Рассмотрим балку с прямоугольным сечением. Мы находим отношение момента разрыва к моменту, когда происходит текучесть в наиболее напряженных волокнах: п мразь^раз®т я^раз P=M,»=G at=I/•момент сопротивления
прямоугольного сечения имеет: Да?’= — б » В(8.30) находим у _nn. От АГ до п 1 * раз — — — — — — — — — — — — — • Подставляя формулу для P、 Таким образом, в случае балки с прямоугольным поперечным сечением разрывной момент равен половине величины момента, который вызывает появление наиболее удаленной ликвидности от нейтрального слоя. В зависимости от формы поперечного сечения волокна 261 коэффициент Р изменяется. Поэтому в двутавровой части, поскольку она меньше прямоугольной части, при расчете балки за пределом упругости необходимо учитывать форму поперечного сечения.
Смотрите также:

