Оглавление:


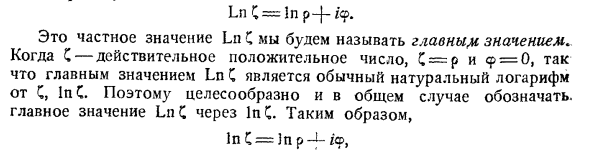



Значения LnC
- Чтобы сделать значения LnC p и 9 полярных координат точки z = C, C = p (cos 9 -j- / sin 9). Пока предположим, что -p может иметь любое положительное значение. Таким образом, C может иметь любое значение, отличное от нуля и отрицательных вещественных чисел. Координаты (x, y) любой точки на пути C являются функцией /, а полярные координаты r и 0 также являются функциями i►. Кроме того, ‘dx — \ — idy_ I x + iy час Ln о C s
Как определено в §229. Где x = rcos6, _y = rsin8 и = (cose + / sin6) (f + frg). Вот так Ln C = J Yitdt + i j g * — [In g] + i [6J, / o ‘o Где [In r] означает разницу значений In r в точках, соответствующих t = t {и t = t0, и [6] имеет такое же значение. Очевидно, ‘ [1ng] = В п-В 1-В п, Тем не менее, значение [G] необходимо рассмотреть более тщательно. Начальным значением b является амплитуда 1, точнее одно из амплитуды 1. 2 для (k — произвольное целое число) 1 год / — с о) JQ X Фаг 52 Та же фигура. 51 Номер.
Во-первых, предположим, что путь интеграции прост от 1 до C сегментов. Людмила Фирмаль
Предположим, что начальное значение 0 равно 2. Рис. 2 51 6 [6] = (2 Al + <p) -2 для = 9 Так что, если интеграл является отрезком прямой, Ln C = In p-j- / 9. Это конкретное значение Ln C называется основным значением. Когда C — положительное действительное число, C = p и 9 = 0, поэтому основным естественным значением Ln C является нормальный натуральный логарифм C, In C.
Поэтому рекомендуется, чтобы в C указывалось основное значение LnC. В С == В р> -ио, Ln C = In p-j- / 9. Это конкретное значение Ln C называется основным значением. Когда C — положительное действительное число, C = p и 9 = 0, поэтому основным естественным значением Ln C является нормальный натуральный логарифм C, In C. Поэтому рекомендуется, чтобы в C указывалось основное значение LnC. В С == В р> -ио,
| Действительные и комплексные криволинейные интегралы | Показательная функция |
| Определение LnC | Общая показательная функция |
Примеры решения и задачи с методическими указаниями
| Решение задач | Лекции |
| Сборник и задачник | Учебник |
- В этом случае путь интеграции обходит источник дважды в положительном направлении. Если вы выбираете путь, который идет вокруг начала координат k раз, [c] = 2Ats + 9 и Ln C = In p-p i (от 2 k до -f-9) Где к положительно. Если путь идет вокруг начала координат в отрицательном направлении (например, путь, показанный пунктирной линией на рисунке 53), вы получите серию похожих значений с отрицательным k. Поскольку | C | = p и угол 2 £ — [- 9 — это разные значения am C, каждое Считайте с помощью | C | —F— / al C — значение LnC.
Из предыдущего обсуждения также ясно, что значения Ln C имеют эту форму. Таким образом, следующий вывод сделан. Общая стоимость LnC При | C | + iamC = lnp + i ‘(2toc + 9) t Где k — произвольное целое число Значение k определяется интегрированием. Если этот путь является прямым отрезком, k = 0 и Ln C = In C = In p i 9. C указывает аргумент функции LnC, а rt и p указывают координаты точки 9 C. Обозначения x *, y, r, b использовались для пути интегрирования и любой точки на ее координатах.
Однако нет причин отказываться от более естественного обозначения, что z является аргументом функции Ln, и затем возвращаться к этим обозначениям. Людмила Фирмаль

