Оглавление:
Задача №1.1.4.
Жонглер бросает вертикально вверх шарики с одинаковой скоростью через равные промежутки времени. При этом пятый шарик жонглер бросает в тот момент, когда первый шарик возвращается в точку бросания. Найти максимальное расстояние 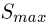 между первым и вторым шариками, если начальная скорость шариков
между первым и вторым шариками, если начальная скорость шариков 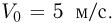 Ускорение свободного падения принять равным
Ускорение свободного падения принять равным 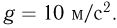 Сопротивлением воздуха пренебречь.
Сопротивлением воздуха пренебречь.
Решение:
Для описания движения шариков выберем координатную систему с началом в точке бросания, направив ось 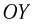 вертикально вверх. Время будем отсчитывать с момента бросания первого шарика.
вертикально вверх. Время будем отсчитывать с момента бросания первого шарика.
Тогда координаты первого и второго шариков будут описываться следующими кинематическими уравнениями:
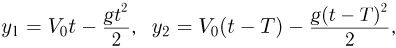
где 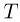 — промежуток времени между бросаниями шариков. Поскольку полное время полета каждого из шариков
— промежуток времени между бросаниями шариков. Поскольку полное время полета каждого из шариков 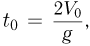 а по условию задачи жонглер бросает пятый шарик в момент, когда первый шарик возвращается в исходную точку,
а по условию задачи жонглер бросает пятый шарик в момент, когда первый шарик возвращается в исходную точку, 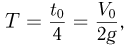 причем первый и второй шарик находятся в полете одновременно при
причем первый и второй шарик находятся в полете одновременно при 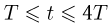 (см. рисунок, на котором сплошными линиями изображены зависимости координат шариков от времени). Расстояние между первым и вторым шариками
(см. рисунок, на котором сплошными линиями изображены зависимости координат шариков от времени). Расстояние между первым и вторым шариками
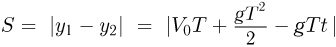 при
при 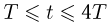
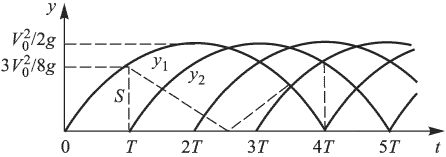
График зависимости этой величины от времени изображен на рисунке штриховой линией. Анализ последнего выражения показывает, что оно достигает максимума при 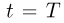 и при
и при 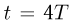 , т.е. в момент бросания второго шарика и в момент возвращения первого шарика в исходную точку. Подставляя в выражение для расстояния между шариками любое из этих значений времени, получаем ответ:
, т.е. в момент бросания второго шарика и в момент возвращения первого шарика в исходную точку. Подставляя в выражение для расстояния между шариками любое из этих значений времени, получаем ответ: 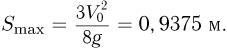
Эти задачи взяты со страницы решения задач по физической механике:
Решение задач по физической механике
Возможно эти задачи вам будут полезны:

