Задача №15.
Жесткий угол 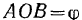 (рис. 32) движется в своей плоскости так, что сторона
(рис. 32) движется в своей плоскости так, что сторона 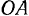 все время проходит через неподвижную точку
все время проходит через неподвижную точку 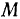 , а сторона
, а сторона 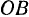 — через неподвижную точку
— через неподвижную точку 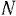 . Найти центроиды этого движения.
. Найти центроиды этого движения.
Решение:
Свяжем подвижную систему отсчета с углом 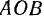 и рассмотрим движение точки
и рассмотрим движение точки 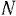 . Абсолютная скорость этой точки равна нулю. В то же время точка
. Абсолютная скорость этой точки равна нулю. В то же время точка 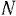 все время остается на прямой
все время остается на прямой 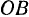 и, следовательно, ее относительная скорость будет направлена вдоль прямой
и, следовательно, ее относительная скорость будет направлена вдоль прямой 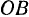 . Но по теореме о сложении скоростей
. Но по теореме о сложении скоростей

и так как
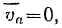
то

то есть переносная скорость направлена тоже вдоль прямой 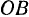 . Но «переносной скоростью является скорость точки подвижной системы отсчета, которая связана жестко с движущимся углом. Отсюда следует, что скорость точки
. Но «переносной скоростью является скорость точки подвижной системы отсчета, которая связана жестко с движущимся углом. Отсюда следует, что скорость точки 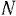 прямой
прямой 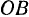 направлена вдоль прямой
направлена вдоль прямой 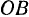 . При помощи аналогичных рассуждений приходим к заключению, что скорость точки
. При помощи аналогичных рассуждений приходим к заключению, что скорость точки 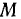 прямой
прямой 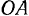 направлена вдоль этой прямой. Зная направления скоростей двух точек движущегося угла
направлена вдоль этой прямой. Зная направления скоростей двух точек движущегося угла 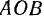 , заключаем, что мгновенный центр вращения угла
, заключаем, что мгновенный центр вращения угла 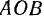 находится на пересечении перпендикуляров к
находится на пересечении перпендикуляров к 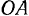 и
и 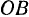 , восстановленных соответственно в точках
, восстановленных соответственно в точках 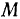 и
и 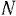 .
.
Обозначим через 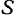 мгновенный центр вращения угла
мгновенный центр вращения угла 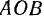 . Из построения нетрудно видеть, что точки
. Из построения нетрудно видеть, что точки 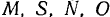 находятся на одной и той же окружности, диаметр которой равен расстоянию
находятся на одной и той же окружности, диаметр которой равен расстоянию  а центр
а центр 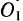 , делит пополам расстояние
, делит пополам расстояние 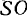 . Очевидно, что
. Очевидно, что 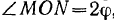 , a
, a 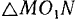 — равнобедренный Отсюда следует, что точка
— равнобедренный Отсюда следует, что точка 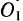 является неподвижной во все время движения, а неподвижной центроидой будет окружность радиуса
является неподвижной во все время движения, а неподвижной центроидой будет окружность радиуса 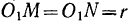 с центром в точке
с центром в точке 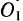 Подвижной центроидой будет окружность радиуса
Подвижной центроидой будет окружность радиуса 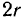 с центром в точке
с центром в точке 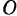 .
.
Задача взята со страницы подробного решения задач по всем темам теоретической механики:
Решение задач по теоретической механике
Возможно эти дополнительные задачи вам будут полезны:

