Оглавление:
Двадцать четыре века назад Зенон Элевтерский, первый греческий философ, указал на невозможность логически последовательного понимания движения тел, хотя и не сомневался в чувственно доказуемой реальности последнего. Дзено сформулировал ряд апорий в связи с проблемой движения. Но не менее интересными в гносеологическом, логическом и особом научном плане являются апории, которые анализировал известный этеец, проблема «много в быту», проблема получения расширенного сегмента в аддитивном синтезе так называемых нерасширенных точек (метрических апорий) и другие. «Трудности, отраженные в апории Зенона, — подчеркнула Яновска, — нельзя считать преодоленными даже в наши дни». Поэтому апории Дзено представляют интерес и для математиков, физиков, философов и ученых некоторых других направлений. Интерес к апории в настоящее время связан с проблемами научного познания пространства, времени, движения и структуры систем в самом широком смысле, а также с проблемами «зарождения» науки в смысле истории зарождения оригинальных представлений о природе («тело», «точка», «место», «мера», «число», «количество», «конечность», «бесконечность» и т.п.). (а) и с точки зрения дискуссий, в которых было уточнено значение этих понятий и которые в конечном итоге стали проблемой математической базы, в целом, принципов точной науки естественных наук.
Биография
Зенон из Элевтерии, родился около 490 г. до н.э.), греческий философ и логик, главным образом известный своими парадоксами, которые носят его имя. Мало что известно о жизни Дзено. Он был родом из греческого города Элея на юге Италии. Платон сообщает, что Зенон был в Афинах и встречался с Сократом. Вероятно около 465 г. до н.э., он изложил свои идеи в книге, которая не пришла к нам. Согласно традиции, Зенон умер, сражаясь с тираном (вероятно, правителем Элеи Неарха). Сведения о нем необходимо собирать поштучно: от Платона, от Зенона, родившегося 60 лет спустя, от рассказов его ученика Аристотеля, от Диогена Лаэртиуса, составившего биографии греческих философов в III веке нашей эры. О Дзено также говорят более поздние комментаторы аристотелевской школы — Фемисий (4-й век), Симплиций и Иоанн Филопон (оба — 6-й век).
Исторические рамки . Чтобы оценить роль Дзено в истории науки и развитии логики, необходимо рассмотреть состояние греческой философии в середине V в. до н.э. Малоазиатские ионийские философы искали происхождение всего, основной элемент, из которого формировалась Вселенная. Каждый решил по отдельности: один присвоил эту роль воде, другой — воздуху, еще один — неизменному, «безграничному» или «неопределенному». Ионийцы считали, что все известные нам виды материи возникают в результате непрерывных процессов выдавливания, разбавления и конденсации основного элемента. Это постоянное изменение было подчеркнуто Гераклитом Эфесским (6-5-й век до н.э.): «Река, в которую мы сейчас входим, не такая, как вчера; все меняется; гармония вселенной — это гармония противоположностей». Наконец, в школе, основанной Пифагором (VI в. до н.э.), в качестве основного элемента подчеркивалось число, а числа рассматривались как дискретные сущности, наделенные пространственным измерением. Парменид, учитель Дзено, критиковал все эти теории. Когда мы рассматриваем любой базовый элемент, мы можем сделать одно из трех утверждений о нем: он существует; его не существует; он существует и его не существует. Третье утверждение само по себе противоречиво; второе также немыслимо, поскольку об отсутствии чего-то нельзя говорить в тех же терминах, в которых оно было описано. Существование небытия даже немыслимо. Таким образом, этот элемент присутствует. Изменение невозможно, так как это означало бы, что первичный элемент не будет распределен везде с одинаковой плотностью, и пустота не может существовать, так как это было бы такое место, где первичный элемент не существует. Значит, вселенная — это неподвижная, неизменная, плотная и единообразная сфера. Всё одно. Отметим, что Парменид приходит к такому выводу исключительно с помощью логики, не прибегая к предположениям или интуиции, характерным для систем его предшественников. Если вывод противоречит чувствам, тем хуже для чувств: внешность обманчива. Дзено продолжил работу, начатую Парменидесом. Его тактика заключалась не в том, чтобы отстаивать точку зрения учителя, а в том, чтобы показать, что еще большие абсурды возникают от утверждений оппонентов. В связи с этим Дзено разработал метод опровержения своих оппонентов серией вопросов. В ответ на них собеседник был вынужден прийти к самым необычным парадоксам, с необходимостью следовать своим взглядам. Этот метод, называемый диалектическим (от греческого «диалегомай» — «говорить»), позже был использован Сократом. Поскольку главными противниками Дзено были пифагорейцы, большинство его парадоксов связано с атомистической концепцией пифагорейства. Поэтому они имеют особое значение для современных атомистических теорий числа, пространства, времени и материи.
Парадоксы Зенона
Парадоксы Зенона известны нам благодаря Аристотелю, который привёл их к критике в своей физике. Он различает бесконечность с точки зрения сложения и бесконечность с точки зрения деления. Время также бесконечно кратное, и бесконечно кратное расстояние может быть покрыто за конечный промежуток времени. Факт противоречия между данными переживаний, с одной стороны, и их ментальным анализом, с другой, выражается Зенона в терминах апорий (от греческого aporia — трудность, недоумение). Апории равнозначны демонстрации того, что 1) логически невозможно думать о множественности вещей и 2) принятие движения приводит к противоречию. По мнению Зенона , попытка представить себе движение приводит к противоречиям, что приводит к выводу, что движение в целом немыслимо.
Парадоксы множественности. Со времен Пифагора время и пространство рассматривались с математической точки зрения как состоящие из множества точек и моментов. Но они также обладают свойством, которое легче воспринимается, чем определяется, а именно «непрерывностью». Посредством ряда парадоксов Зенон попытался доказать невозможность разделения преемственности на точки или моменты. Его аргумент сводится к следующему: предположим, мы разделимся до конца. Тогда один из двух результатов верен: либо мы имеем в остатке как можно меньшие части или величины, которые неделимы, но бесконечны по количеству, либо деление привело нас к частям без величины, т.е. превратило нас в ничто, так как преемственность, будучи однородной, должна быть разветвленной везде, а не такой, чтобы в одной ее части была разветвленная, а в другой — не разветвленная. Оба результата, однако, ложны: во-первых, потому что процесс деления не может считаться завершенным до тех пор, пока в оставшейся части есть части, обладающие величиной; во-вторых, потому что в таком случае первоначальное целое образовалось бы из ничего. Зенон , поддерживая своего учителя, старался доказать, что все вещи должны быть единым и неподвижным. Он основывал свое доказательство на бесконечной делимости всей преемственности. Точно, он утверждал, что если существо не является единым и неделимым, но может быть разделено на многих, то одно в существе вообще не будет единым, а если ничего в существе не является единым, то и многие тоже невозможны, так как многие состоят из множества единиц. Таким образом, сущность не может быть разделена на множество, следовательно, есть только Один. Simplicius также приписывает Зенон следующий аргумент: «Если множество существует, то оно должно быть точно таким, как есть, не больше и не меньше». Если, однако, все будет так, как есть, то это будет конечным. Но если есть множество, то вещи бесконечны по количеству, ибо между ними всегда будут найдены другие, а между этими другими и более. Поэтому вещи бесконечны по количеству». Дискуссия о множественности была направлена против соперничающей школы с Элеатикой, скорее всего, пифагорейцами, которые считали, что ценность или величина формируется из неделимых частей. Зенон считал, что эта школа верила в то, что непрерывные количества и до бесконечности делимы и конечны.
Парадоксы движения. Аргументы о движении известны нам только из краткого анализа Аристотеля в области физики и комментариев Симплиция, Филопона и Фемиция. Симплиций утверждает, что у него была работа Зенона , и его комментарии о количестве подтверждают это. Но в «Комментариях к движению», хотя из некоторых замечаний видно, что он знал и эту часть произведения, нет ничего нового или отличного от Аристотеля, возможно, из-за признанной сложности этих аргументов. Всего нам известны четыре апоры, связанные с парадоксами движения: «Дихотомия» и «Ахиллес» обращаются к сложности понимания движения в предположении о неограниченной делимости пути и времени, в то время как «Стрела» и «Этап» выражают трудности в предположении об обратном, а именно в предположении о неделимых элементах пути и времени (проблема квантов пространства и времени).
Дихотомия Апория
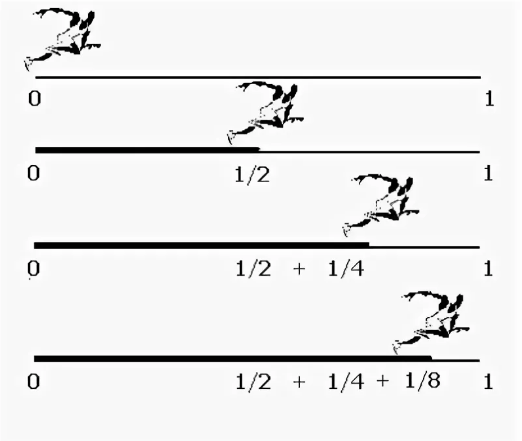
Формулировка апории: Пусть AB будет отрезком длиной 1, а точка M перемещается из точки A в точку B. Перед достижением B он должен пройти через бесконечное множество «средних точек» A1, A2, … … «отсчет», поэтому точка Б никогда не достигается. Движущееся тело никогда не достигнет конца пути, так как сначала оно должно дойти до середины пути, затем до середины остальной части пути, и так далее. Анализ Апории: Первый парадокс гласит, что прежде чем движущийся объект сможет пройти заданное расстояние, он должен достигнуть половины этого расстояния, затем половины оставшегося, и так далее, до бесконечности. Так как при многократном сокращении заданного расстояния каждый отрезок остается конечным, а количество таких отрезков бесконечно, то заданное расстояние не может быть покрыто за конечное время. Более того, этот аргумент применим к любому расстоянию, независимо от того, насколько оно маленькое, и к любой скорости, независимо от того, насколько большое. Таким образом, движение невозможно. Бегун даже не может двигаться. Simplicius, подробно комментируя этот парадокс, отмечает, что здесь бесконечное количество прикосновений должно быть сделано за конечное время: «Тот, кто прикасается к чему-то, считается, как было, но бесконечное количество не может быть ни подсчитано, ни перечислено». Или, как выразился Филопон, «бесконечность абсолютно бесконечна». Аристотель рассматривал «дихотомию» как обман, а не парадокс, полагая, что ее смысл отрицается «ложной предпосылкой, как будто невозможно пройти или коснуться бесконечного числа очков в течение конечного периода времени». Фемиций также считает, что «Дзено либо не знает, либо делает вид, что знает, когда он предполагает, что ему удалось положить конец движению, сказав, что это невозможно для движущегося тела, чтобы пройти через бесконечное число позиций в конечный период времени». Анализируя эту апорию, можно заметить ошибку деления пространства Зенона на бесконечность. На самом деле пространство и время бесконечно делимы, но вовсе не бесконечно разделены. Особенно важно отметить, что пространство и время на самом деле не бесконечно делимы, а только потенциально делимы на бесконечность. Утверждение Зенон в этой апории о невозможности движения говорит против всех законов восприятия мира, как бы мало они ни были выбраны. Однако парадокс не решается только вычислениями. Ведь сначала нужно доказать утверждение, что расстояние — это скорость, умноженная на время, а это невозможно сделать без анализа того, что означает мгновенная скорость, понятие, лежащее в основе третьего парадокса движения. Таким образом, можно сделать вывод, что этот парадокс основан на сложности суммирования бесконечного числа постоянно уменьшающихся величин и невозможности интуитивно представить, что эта сумма соответствует конечной величине. Большинство источников, объясняющих эти парадоксы, утверждают, что Зенон полностью отрицал возможность движения, но иногда утверждают, что аргументы, которые он защищал, были направлены лишь на то, чтобы доказать несовместимость движения с его постоянно оспариваемым понятием континуитета как множественности. В «Дихотомии» и «Ахиллесе» утверждается, что движение невозможно при предположении, что пространство бесконечно делится на точки, а время — на моменты. В двух последних парадоксах движения утверждается, что движение одинаково невозможно, если исходить из противоположного предположения, а именно, что разделение времени и пространства завершается неделимыми единицами, т.е. время и пространство имеют атомную структуру. Известный философ-интуитивист А. Бергсон высказывает такое мнение об этой апории: «Вещь можно разделить, но не акт». По Бергсону, Зенон путает процесс движения, из которого каждое действие неделимо, с бесконечным делимым пространством. Но вряд ли можно согласиться с Бергсоном. Для Зенон кажется бесспорным, что движение — это процесс. Он говорит, в конце концов, не о трудностях введения секций пространства, которые являются полными в их данности, а о непостижимости процесса их прохождения. Либо движение описывается как процесс, как ряд последовательных операций, либо действий по реализации движения, либо придется признать, что любая попытка такого описания неизбежно приводит к противоречиям, что означает логическую невозможность движения.
Влияние Зенона на философию Древней Греции
Зенон придал своим апориям ярко выраженный физический смысл: он направил их против возможности движения. Главный вопрос — это связь между математической моделью и реальным физическим пространством.
В апории Зенон пространство предполагается располагать так же, как и в малом, как и в большом; факты из поля движения множеств определенного порядка переносятся во все множества. Между тем, в соответствии с современными физическими точками зрения, физические величины вовсе не делимы на бесконечность. Современная физика раскрывает все больше и больше удивительных фактов о структуре микромира. D. Гилберт и Пи. Бернис в своей книге «Основы математики» (1934) писал, что решение «дихотомии» парадокса «состоит в том, что нам не обязательно верить, что математическое пространственно-временное представление движения имеет физический смысл для произвольно малых интервалов пространства и времени»; Скорее, у нас есть все основания полагать, что эта математическая модель экстраполирует факты из некоторой области опыта, а именно, из области движений в масштабах, еще доступных для нашего наблюдения, экстраполированных просто в смысле формирования идей, точно так же, как механика континуума выполняет экстраполяцию Аналогичным образом, во всех случаях, когда существует вера в возможность непосредственно видеть (актуальную) бесконечность через опыт или восприятие. .. Более тщательное расследование затем показывает, что бесконечность не была дана нам вообще, а только была интерполирована или экстраполирована каким-то интеллектуальным процессом».
Апории Зенон подняли очень глубокие и сложные вопросы. Так как же древняя наука ответила им? В частности, как был решен вопрос о допустимости использования в математике действительных бесконечно больших и действительных бесконечно малых величин? Точки зрения древней математики и дискуссии в ней можно оценить по косвенным свидетельствам, главным образом, Аристотеля и других философов.
Через четыре парадокса Зенон очень хорошо достигает того, чего хотел. Он логически строго показывает, что с пифагорейскими представлениями о движении, пространстве и времени что-то не так. Эти демонстрации Зенон не убедили более поздних мыслителей согласиться с выводами Парменида, но они привели этих мыслителей к уважению формальной логики и к тому, чтобы увидеть новые возможности ее применения. Они также привели, конечно, к попыткам переформулировать пифагорейские концепции, чтобы устранить противоречия, на которые указывал Зенон . Эти попытки принимали разные формы: Анаксагор отказался от идеи отдельных точек и заменил ее непрерывной последовательностью, Аристотель полностью отделил арифметику от геометрии, а атомистическая теория была основана на четком разграничении физической и математической «делимости».
На странице рефераты по философии вы найдете много готовых тем для рефератов по предмету «Философия».
Читайте дополнительные лекции:
- Предпосылки появления философии
- Эрнст Шлиермахер и его философия
- Проблема происхождения сознания человека
- Развитие информационных технологий и автоматизация проектирования
- Абхинавагупта, индийский философ
- Идея общественно-исторической закономерности
- Душа в средневековой философии индии
- Концепция «воли к власти» Ф. Ницше
- Гносеология Локка
- Прагматизм

