Оглавление:


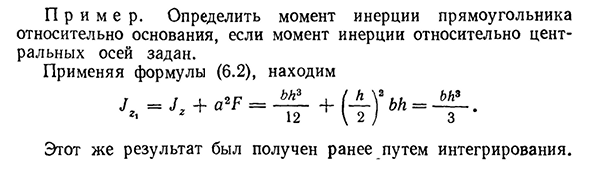

Зависимость между моментами инерции относительно параллельных осей
- Связь между моментами инерции Относительно параллельной оси Предположим, что дан момент инерции относительно осей Oz и Oh и
площадь фигуры. Определим момент инерции для новых осей O ^ Zi и O ^ i. С рисунка. Вы можете установить связь между 157 координатами: yi = Y4-a; = z4-B. 4-а)
2dF = dF == Jz2aSz + a2F получается Людмила Фирмаль
с использованием общей формулы для аксиального момента инерции. 174 = J y4-2 & Sy4-62F установили, что так же, как мбжно. Из-за центробежного момента инерции имеем J, 121 = jy xzxdF = J (y + a) (g4-b) dF = J zydF-Fab J dF + 4-AJ zdF + b J ydF = J zy4-abF4-aSy4-БСЗ. В этих
уравнениях SzHSy представляет статический момент фигуры вокруг осей Oz и Oh. Если эти оси центрированы, статический момент для них равен нулю. S z = 0; S y = 0. И момент инерции формулы Что касается осей, параллельные центральным будут выглядеть так:
- Двадцать один «/ 21 = Jz4-a2 / 7; J u. = L4» b2F \ Jz.y. = * ^ zy4 «abF. Уравнение (6.?) Часто используется для расчета момента инерции сложных фигур. Добавлены первые две строки уравнения (6.2) и дано / P1 = Jz. + J y. Получаем инерционную формулу Для полярного момента между J pie = J9 4- (a2 + * 2) F. Учитывая моменты инерции
относительно любой оси, решая уравнения (6.2) для Jz, Jy и Jzy для центральной оси, параллельной этим осям: L = Jz, -A2P- J = -62p. -abF (6.3) Из этих уравнений видно, что момент инерции относительно центральной оси имеет наименьшее значение по сравнению с моментом инерции относительно других параллельных осей.
175P R и я Р. Если задан момент инерции относительно центральной оси, Людмила Фирмаль
определите прямоугольный момент инерции относительно основания. Применяя уравнение (6.2), J = J + a’-F = + W3 6 / g = _ ^ _. g> 2 12 \ 2) 3 Такой же результат был получен ранее при интегрировании.
Смотрите также:

