Оглавление:
Затухающие колебания материальной точки
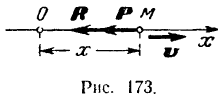
В реальных условиях колеблющаяся материальная точка всегда испытывает сопротивление своему движению. Рассмотрим случай, когда на точку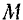 
(рис. 173) действуют восстанавливающая сила 
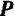, модуль которой 
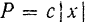, и сила сопротивления среды 
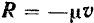, пропорциональная первой степени скорости точки.
Примем опять прямую, по которой движется точка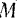 
, за ось 
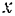и за начало 
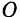координат — положение равновесия точки .
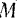Так как проекция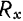 
силы 
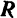на ось 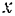всегда будет иметь знак, противоположный знаку проекции 
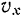скорости точки на ту же ось, то
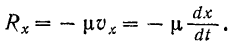
Следовательно, проекция на ось 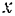равнодействующей всех сил, приложенных к точке :
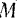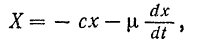
и дифференциальное уравнение движения этой точки принимает вид
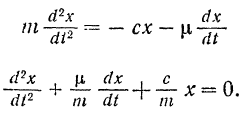
Обозначив
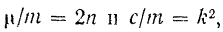
получим уравнение
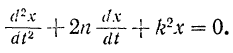
Постоянный коэффициент
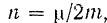
характеризующий сопротивление среды, имеет размерность:
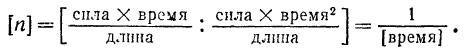
Круговая частота свободных колебаний точки имеет размерность
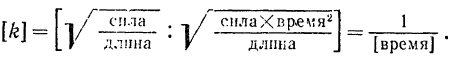
Так как коэффициенты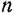 
и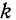 
имеют одинаковую размерность, то их, очевидно, можно сравнивать между собой.
Для интегрирования дифференциального уравнения (120) составляем характеристическое уравнение
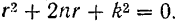
Корни этого уравнения:
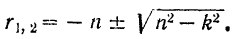
Ограничимся рассмотрением только случая малого сопротивления, когда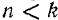 
. В этом случае корням характеристического уравнения можно придать вид
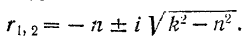
Так как корни характеристического уравнения являются комплексными, то общее решение дифференциального уравнения (120) будет иметь вид
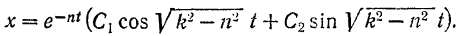
Вводя вместо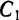 
и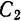 
новые постоянные 
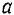и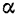 
и полагая при этом 
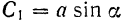и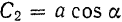 
, получим уравнение движения точки 
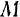в виде
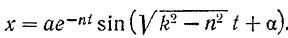
Колебания, происходящие по данному закону, называются затухающими, так как благодаря множителю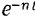 
их амплитуда 
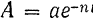с течением времени непрерывно уменьшается.
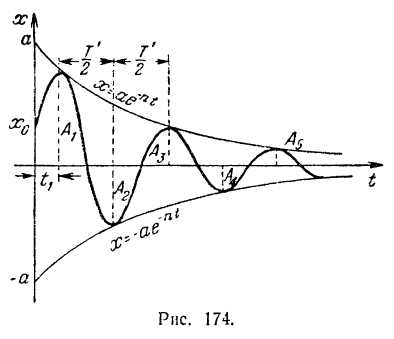
Графиком затухающих колебании (рис. 174) является затухающая синусоида, заключенная между двумя симметричными кривыми
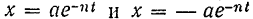
(так как
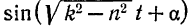
изменяется в пределах от—1 до +1). Промежуток времени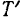 
между двумя последовательными крайними положениями точки по одну сторону от положения ее равновесия условно называют периодом затухающих колебаний. Он равен периоду
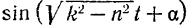
и, следовательно,
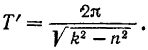
Как было найдено ранее, период свободных колебаний точки
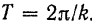
Так как
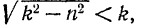
то
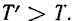
Таким образом, период затухающих колебаний точки больше периода свободных колебаний, совершаемых ею под действием той же самой восстанавливающей силы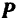 
, но при отсутствии сопротивления.
Однако в случае малых сопротивлений 
влиянием сопротивления на величину периода колебаний практически можно пренебречь, полагая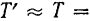 
.
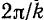Пусть в момент времени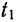 
амплитуда затухающих колебаний равна 
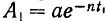. Найдем последовательные значения 
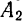и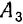 
переменной амплитуды через промежутки времени, равные 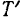— периоду колебании (рис. 174):
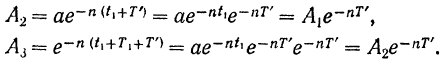
Аналогичным путем мы, очевидно, получим для двух любых последовательных значений амплитуды:
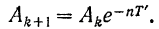
Число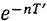 
называется декрементом колебаний, натуральный логарифм декремента, т. е. величина —
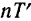, называется логарифмическим декрементом.
Коэффициент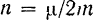 
называется коэффициентом затухания.
Из найденного выше следует, что последовательные значения амплитуд затухающих колебаний составляют убывающую геометрическую прогрессию, знаменатель которой равен декременту этих колебаний.
Так как время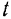 
входит в показатель степени множителя 
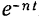, то амплитуда 
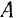затухающих колебаний непрерывно и весьма быстро (даже при малом 
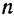) уменьшается.
Пример задачи:
Материальная точка совершает прямолинейные колебания под действием силы, пропорциональной расстоянию этой точки от неподвижного центра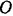 
. Сила сопротивления среды пропорциональна первой степени скорости. Период колебания точки 
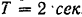. После двух полных колебаний амплитуда колебаний точки уменьшилась в 16 раз. Определить закон движения точки, если в момент, когда точка находилась в положении покоя, ей была сообщена скорость 
.
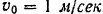Решение:
Если прямую, по которой движется точка, принять за координатную ось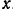 
, а за начало координат — неподвижный центр 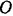, то уравнение затухающих колебаний точки имеет вид (121):
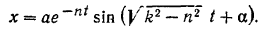
Найдем значения всех коэффициентов, входящих в это уравнение. По формуле (122) период затухающих колебаний
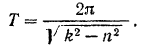
Отсюда круговая частота колебаний
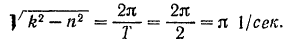
Последовательные значения амплитуд затухающих колебаний составляют убывающую геометрическую прогрессию, знаменатель которой равен декременту 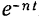этих колебаний. Следовательно,
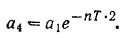
По условию задачи
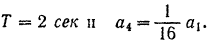
Отсюда
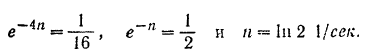
Для определения наибольшей амплитуды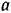 
и начальной фазы 
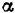колебаний воспользуемся начальными условиями: при
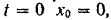
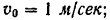
при
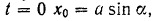
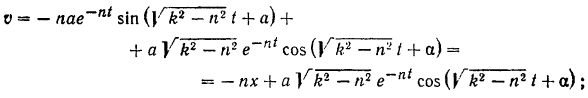
при
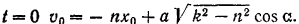
Решая совместно эти уравнения и подставляя данные значения
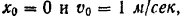
находим:
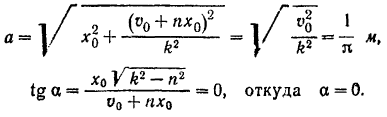
Подставляя все найденные значения в уравнение (121) затухающих колебаний, получим закон движения данной точки:
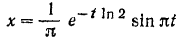
или, так как
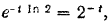
то
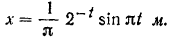
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Теоретическая механика — задачи с решением и примерами
Возможно вам будут полезны эти дополнительные темы:
| Прямолинейные колебания материальной точки |
| Свободные колебания материальной точки с примером решения |
| Вынужденные колебания материальной точки с примером решения |
| Механическая система |
