Создатель теории приближенных вычислений А. Н. Крылов говорил: «При производстве всяких численных вычислений надо руководствоваться правилом: точность вычислений должна соответствовать точности данных и той практической потребности, для которой вычисления производятся». Ему же принадлежат слова: «Помните, что каждая неверная цифра — это ошибка, всякая лишняя цифра — это пол-ошибки».
Приближенные числа записываются, как правило, при помощи десятичных дробей. Между записью приближенных и точных чисел есть различия. Если перед нами точное число, то вес его цифры являются верными, точными. Что же касается приближенного числа, то некоторые его цифры верны, а другие являются сомнительными.
Цифра десятичного разряда приближенного числа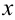 
приближения 
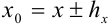называется верной, если в том же десятичном разряде чисел 
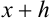и 
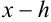стоит эта же цифра. В противном случае она называется сомнительной.
Проверку на верные и сомнительные цифры нужно начинать слева направо с наивысшего разряда. Все цифры, стоящие правее первой найденной сомнительной цифры, автоматически считаются сомнительными.
Пример №45.4.
Найдите верные и сомнительные цифры в записи числа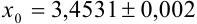 
.
Решение:
Поскольку 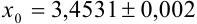, запишем диапазон возможных значений 
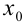в виде двойного неравенства:
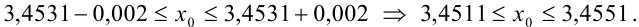
Начинаем проверку на верные и сомнительные цифры с наивысшего разряда — единиц. Видим, что цифры 3,45 одинаковы в левой и правой части двойного неравенства (т.е. в запис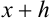и и 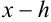), следовательно, по определению в записи приближенного числа 3,4531 эти цифры являются верными.
Цифры в разряде тысячных в правой и левой части двойного неравенства отличаются (1 и 5), следовательно, в записи приближенного числа 3,4531 цифра 3, стоящая в разряде тысячных, и цифра 1, стоящая за ней, являются сомнительными.
Итак, точное число 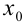обязательно начинается с цифр 3,45. Какие цифры стоят в остальных разрядах числа, точно сказать невозможно.
Ответ:
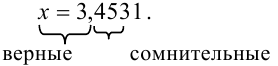
Для записи приближенных чисел существуют следующие правила:
- Оставлять в записи числа только верные цифры.
- Если в десятичной дроби последние верные цифры нули, то их надо выписывать.
- Если число содержит на конце целой части сомнительные цифры, то они должны быть заменены на
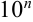, где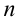 
— число цифр, которые нужно заменить. - Граница абсолютной погрешности числа, содержащего только верные цифры, равна единице последнего разряда.
Проиллюстрируем применение данных правил на конкретных примерах.
1. Поскольку в записи числа следует оставлять только верные цифры, то в примере 45.4 точное значение 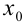будет записано следующим образом: 
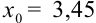. В этом случае граница абсолютной погрешности 
.
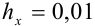2. Если задано число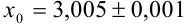 
, то нетрудно показать, что в записи приближенного числа 3,005 цифры 3,00 являются верными, а 5 — сомнительной. Для записи точного числа 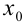выпишем все его верные цифры, включая нули на конце: 
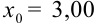. Эта запись показывает, что граница абсолютной погрешности равна единице последнего разряда, т.е. 0,01. Если бы мы записали это число как 
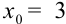, то граница абсолютной погрешности была бы равна 1, а это значительно более низкая точность, чем заданная в примере 0,01.
3. Пусть задано число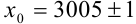 
. В записи приближенного числа 3005 цифры 300 являются верными, а 5 — сомнительной. Для записи точного числа 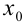выпишем вес его верные цифры 300, а вместо одной сомнительной цифры 5 запишем умножение на 
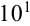, поскольку заменяем только одну цифру. Тогда 
.
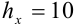В науке принято записывать числа в стандартном виде, т.е. в ви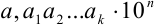де 
, где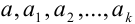 
— цифры, причем 
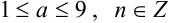(в целой части числа стоит только одна цифра, отличная от нуля). Число 
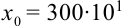в стандартном виде будет представлено как 
.
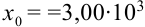Значащими цифрами числа называют все его верные цифры, за исключением нулей, стоящих левее первой отличной от нуля цифры.
Например, число 0,712 содержит три значащие цифры: 7, 1, 2. Число 0,00012 — две значащие цифры: 1 и 2. Число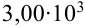 
— три значащие цифры: 3, 0, 0.
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
| Абсолютная погрешность. |
| Относительная погрешность. |
| Погрешности вычислений с приближенными данными. |
| Понятие алгебраического и трансцендентного уравнения и методов их приближенного решения. |
