Оглавление:
Замена в неравенствах множителей вида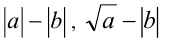 
множителями эквивалентного знака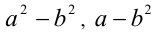 
Рассмотрим приём, позволяющий избавляться от модулей в определённой группе задач и, тем самым, существенно их упрощать. Он непосредственно следует из рассмотренного выше приёма умножения на выражение, сопряжённое к выражению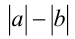 
.
Пусть требуется решить неравенство, в котором с одной стороны от знака неравенства (он может быть произвольным) находится произведение (частное) нескольких сомножителей, а с другой стороны — число нуль. К этой группе, в частности, относятся неравенства, решаемые методом интервалов. Например, это может быть неравенство вида
Пусть, кроме того, хотя бы один из сомножителей имеет вид разности двух модулей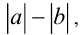 
где 
, 
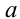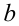— некоторые выражения, зависящие от неизвестной (-ых). Ради определённости будем считать, что это А :
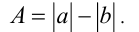
Если умножить обе части неравенства (1) на положительное выражение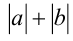 
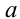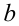(будем дополнительно считать, что и одновременно не обращаются в нуль), то получим равносильное неравенство, в котором вместо множителя 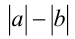появился множитель 
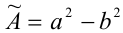, не содержащий модулей. Таким образом, решение исходного неравенства (1) оказалось сведено к равносильному неравенству
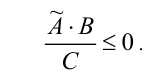
Выражения 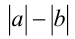и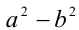 
всегда имеют один и тот же знак, и одновременно обращаются в нуль. Поэтому этот подход часто называют методом замены множителей на множители эквивалентного знака.
В действительности область применимости данного приёма гораздо шире. Пусть 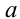и 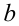— любые неотрицательные (на ОДЗ) выражения, одновременно не обращающиеся в нуль (случай их одновременного обращения в нуль всегда можно рассмотреть отдельно). Тогда можно утверждать, что выражения 
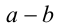и 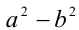имеют один и тот же знак, и, следовательно, в неравенствах указанного типа сомножитель вида 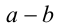можно заменять выражением вида .
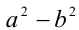В частности, сомножители вида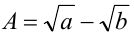 
или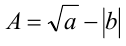 
с успехом могут быть заменены выражениям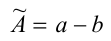и 
и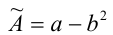 
соответственно (при условии 
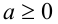, а в первом случае и 
).
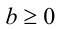Рассмотрим примеры применения этого — иногда очень эффективного — метода.
Пример №278.
Решить неравенство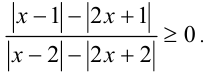 
Решение:
Применяя указанный выше приём, приходим к равносильному неравенству и решаем его:
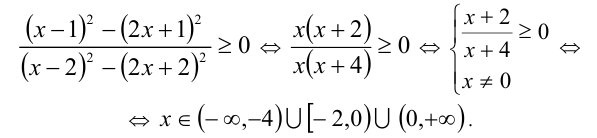
Пример №279.
Решить неравенство
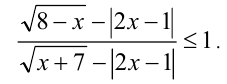
Решение:
ОДЗ: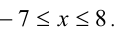
Перенесём все слагаемые в одну сторону:
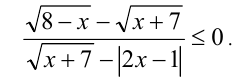
Так как на ОДЗ выражения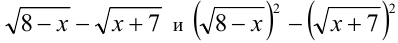 
а также выражения 
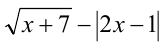и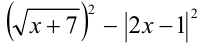 
имеют одинаковые знаки (и одновременно обращаются в нуль), то приходим к равносильному (на ОДЗ), но более простому неравенству
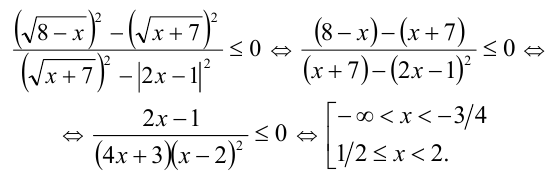
Пересекая с ОДЗ, получаем ответ. Ответ: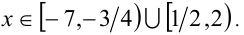 
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:
