Оглавление:
Замена переменных: рационализирующие подстановки
Метод замены переменных часто позволяет преобразовать иррациональное уравнение (неравенство) к рациональному виду. В этом случае говорят о рационализации уравнений (неравенств), а используемые подстановки называют рационализирующими.
Рассмотрим наиболее типичные алгебраические, тригонометрические и гиперболические подстановки. Обозначим символом R(x,y) рациональную дробь, т.е. дробь, числитель и знаменатель которой являются многочленами относительно переменных x и у .
Рационализация выражений вида 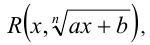 содержащих линейную иррациональность
содержащих линейную иррациональность 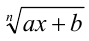 , где а и b— постоянные
, где а и b— постоянные 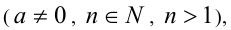 осуществляется с помощью алгебраической подстановки
осуществляется с помощью алгебраической подстановки 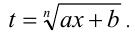 Возводя обе части этого равенства в степень n , получим
Возводя обе части этого равенства в степень n , получим 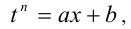 откуда
откуда 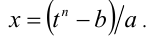 Переходя в R от переменной x к переменной t, получим рациональное выражение
Переходя в R от переменной x к переменной t, получим рациональное выражение
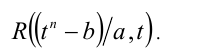
Аналогичным образом рационализируются выражения вида
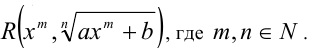
При этом используется подстановка 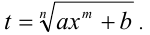
Пример №245.
Решить уравнение 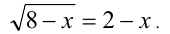
Решение:
Сделаем рационализирующую подстановку 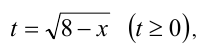 откуда находим
откуда находим 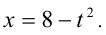 Подставим в уравнение:
Подставим в уравнение: 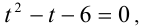 решая которое, находим корни
решая которое, находим корни 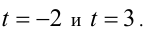 Поэтому
Поэтому 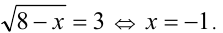
Рационализация выражений вида 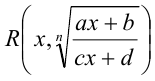 , содержа-щих дробно- линейную иррациональность
, содержа-щих дробно- линейную иррациональность 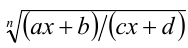 , где a ,b ,c, d — постоянные
, где a ,b ,c, d — постоянные 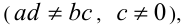 осуществляется с помощью алгебраической подстановки
осуществляется с помощью алгебраической подстановки 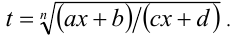
Пример №246.
Решить неравенство
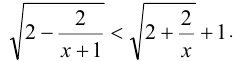
Решение:
Сначала преобразуем неравенство к виду
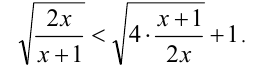
Сделаем подстановку 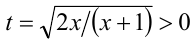 и получим рациональное неравенство относительно t :
и получим рациональное неравенство относительно t :
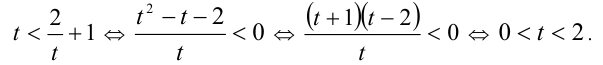
Осталось сделать обратную подстановку
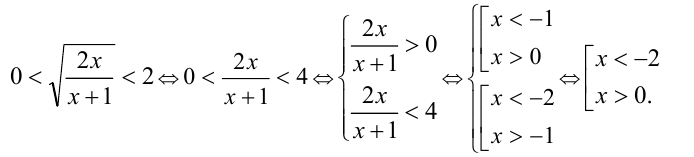
Иррациональные уравнения вида 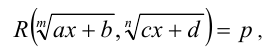 где a ,b ,c ,d , p — некоторые числа
где a ,b ,c ,d , p — некоторые числа 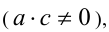
 двойной подстановкой
двойной подстановкой 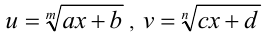 сводятся к системе двух рациональных уравнений
сводятся к системе двух рациональных уравнений
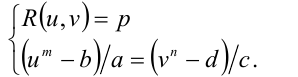
Пример №247.
Решить уравнение 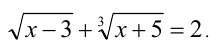
Решение:
Выполним двойную (рационализирующую) подстановку 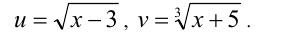
Уравнение примет вид u+v=2 Составим ещё одно уравнение относительно неизвестных u и v . Так как 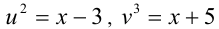 то, исключая x находим:
то, исключая x находим: 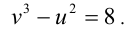 Добавляя это уравнение к исходному уравнению, получим систему уравнений с двумя неизвестными u и v:
Добавляя это уравнение к исходному уравнению, получим систему уравнений с двумя неизвестными u и v:
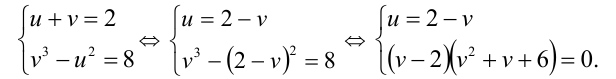
Система имеет единственное решение u = 0, v = 2, откуда находим x =3.
Пример №248.
Решить уравнение 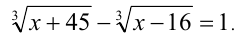
Решение:
Положим 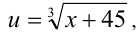
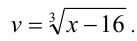 Тогда
Тогда 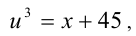
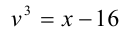 и
и 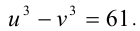 Таким образом, приходим к системе двух алгебраических уравнений с двумя неизвестными
Таким образом, приходим к системе двух алгебраических уравнений с двумя неизвестными
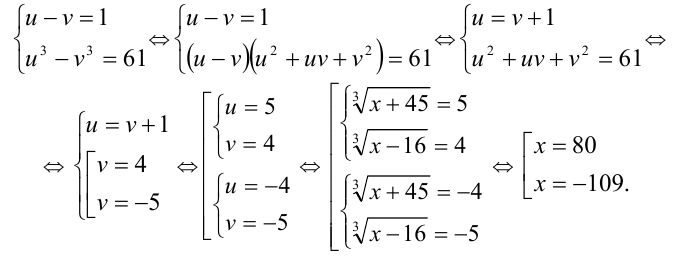
Пример №249.
Решить уравнение 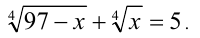
Решение:
Аналогично двум предыдущим примерам, положим 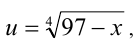 Исходное уравнение примет вид
Исходное уравнение примет вид 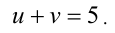 Заметим, что
Заметим, что 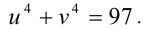 Имеем систему
Имеем систему
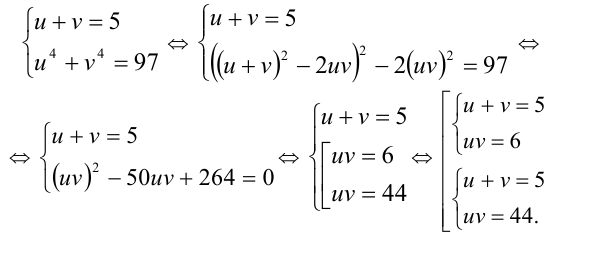
Вторая система решений не имеет, а первая даёт два решения:
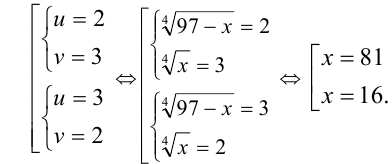
Ответ: 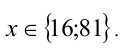
Иногда при рационализации иррациональных уравнений и неравенств оказываются эффективными тригонометрические подстановки. Здесь следует иметь в виду следующие рекомендации.
Рационализацию выражений вида 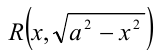
рекомендуется делать с помощью подстановки 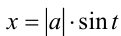 , где
, где 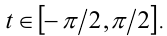 Тогда
Тогда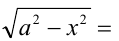
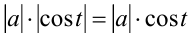 , так как на промежутке
, так как на промежутке 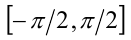 косинус принимает неотрица-тельные значения. При этом алгебраическое иррациональное выражение
косинус принимает неотрица-тельные значения. При этом алгебраическое иррациональное выражение 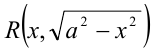 преобразуется к виду тригонометриче-ского, но уже рационального выражения
преобразуется к виду тригонометриче-ского, но уже рационального выражения
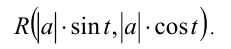
Также в этом случае можно сделать подстановку 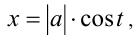 где
где 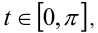 и тогда вместо иррациональной функции
и тогда вместо иррациональной функции 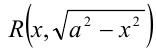 получили бы рациональную тригонометрическую функцию [20]
получили бы рациональную тригонометрическую функцию [20]
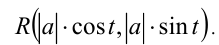
Пример №250.
Решить уравнение
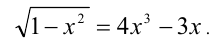
Решение:
Сделаем тригонометрическую подстановку 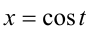 ,
, 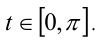
Получим
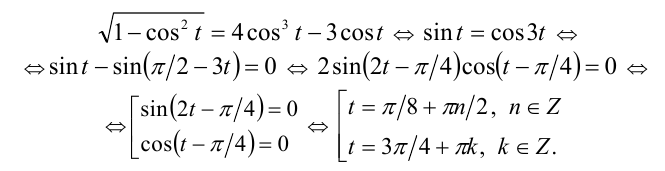
Из первой серии в отрезок 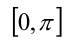 попадают два значения
попадают два значения 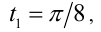
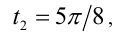 а из второй
а из второй 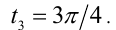 Им соответствуют
Им соответствуют 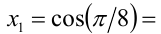
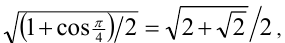
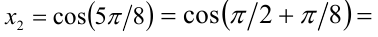
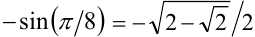 ,
,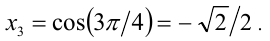
Пример №251.
Решить уравнение
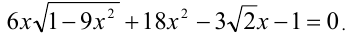
Решение:
Сделаем тригонометрическую подстановку 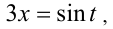 где
где 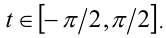 Тогда
Тогда 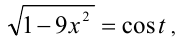
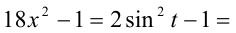
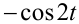 и уравнение примет вид:
и уравнение примет вид:
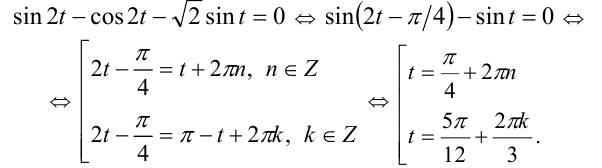
Из 1-й серии в отрезок 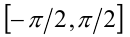 попадает одно значение
попадает одно значение 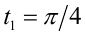 , из 2-й два значения
, из 2-й два значения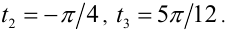
Следовательно, уравнение имеет три решения:
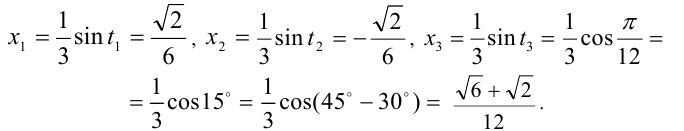
Для рационализации выражений вида 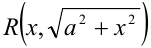 применя-ют подстановку
применя-ют подстановку 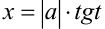 , где
, где 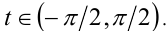 В этом случае
В этом случае
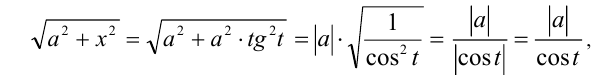
так как на рассматриваемом интервале косинус положителен. В результате выражение 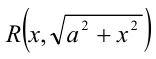 преобразуется к виду
преобразуется к виду 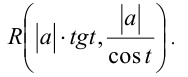
В данной ситуации можно было также сделать подстановку
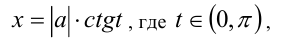
или гиперболическую подстановку 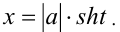 В последнем случае
В последнем случае
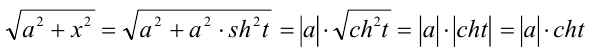
(так как 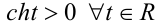 ).
).
Пример №252.
Решить уравнение 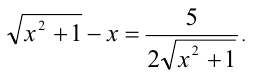
Решение:
Воспользуемся тригонометрической подстановкой вида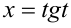 , где
, где 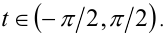 Тогда уравнение примет вид
Тогда уравнение примет вид
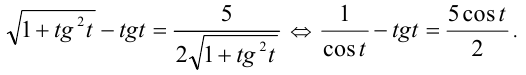
Умножая уравнение на 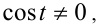 получим равносильное уравнение
получим равносильное уравнение
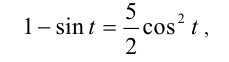
которое сводится к квадратному уравнению относительно 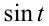 :
:
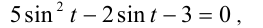
откуда находим 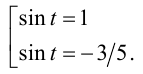 Случай
Случай 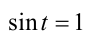 невозможен, так как
невозможен, так как 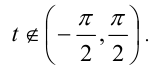 Итак,
Итак,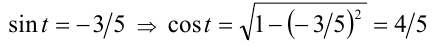 и, следовательно,
и, следовательно,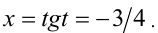 Ответ:
Ответ: 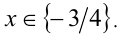
Для рационализации выражений вида 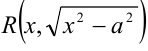 применяют одну из следующих тригонометрических подстановок:
применяют одну из следующих тригонометрических подстановок:
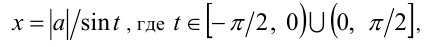
или
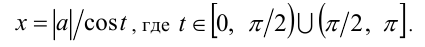
В первом случае радикал упрощается следующим образом:
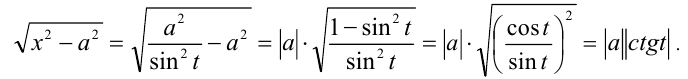
Для рационализации данного выражения 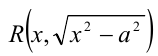 можно также использовать гиперболическую подстановку
можно также использовать гиперболическую подстановку 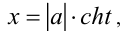 если
если 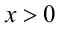 , и подстановку
, и подстановку 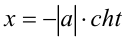 , если
, если 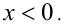 В первом случае имеем
В первом случае имеем
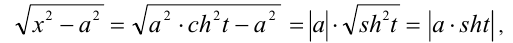
и выражение приводится к рациональному виду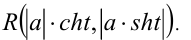
Существуют приёмы, позволяющие рационализировать выражения с квадратичными иррациональностями общего вида
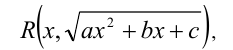
где 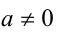 ,
, 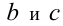 — постоянные. В частности, уравнения вида
— постоянные. В частности, уравнения вида
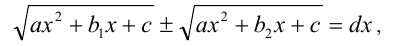
а также вида
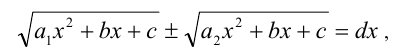
где 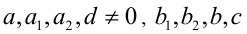 — постоянные, заменой
— постоянные, заменой
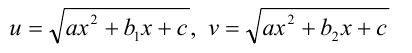
соответственно,
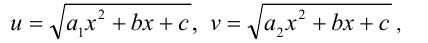
сводятся к системе рациональных уравнений.
Пример №252.
Решить уравнение
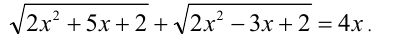
Решение:
Положим 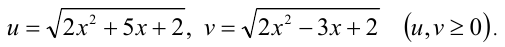
Тогда уравнение сводится к системе
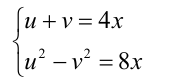
(из первого уравнения  ), откуда, как следствие, получаем
), откуда, как следствие, получаем
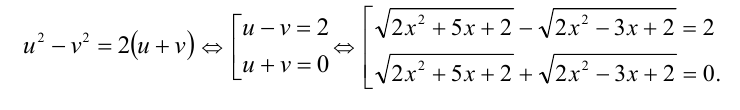
Для решения первого из уравнений сложим его с исходным:
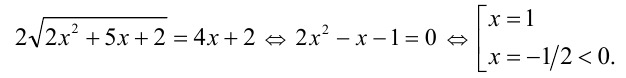
Второе уравнение совокупности неотрицательных корней не имеет. Проверка показывает, что x = 1 удовлетворяет исходному уравнению.
Ответ: 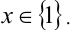
Рассмотрим ещё один пример с квадратичной иррациональностью.
Пример №253.
Решить уравнение
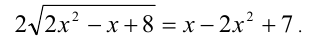
Решение:
Положим 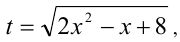 тогда уравнение сводится к системе
тогда уравнение сводится к системе
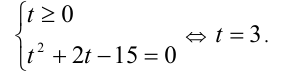
Выполняя обратную подстановку, получим уравнение
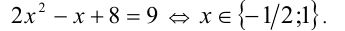
Рационализирующие подстановки используются также в задачах с несколькими неизвестными, например при решении систем.
Пример №254.
Решить систему
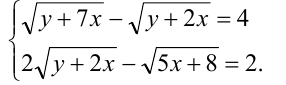
Решение:
Сделаем тройную подстановку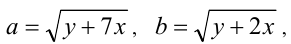
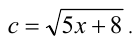 Составив самосто-ятельно третье уравнение, зависящее только от а,b и c (и не зависящее от x и y), приходим к несложной системе целых алгебраических уравнений
Составив самосто-ятельно третье уравнение, зависящее только от а,b и c (и не зависящее от x и y), приходим к несложной системе целых алгебраических уравнений
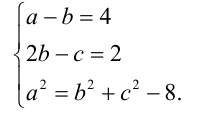
Система имеет единственное неотрицательное решение 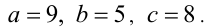
Выполняя обратную подстановку, находим решения: 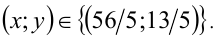
9.Выше мы рассматривали различные способы рационализации алгебраических уравнений. В общем случае решаемое уравнение или неравенство с радикалами может не иметь алгебраический вид. В этой ситуации также могут быть использованы рационализирующие подстановки. Например, в следующей задаче двойная подстановка преобразует неравенство показательного вида с радикалами в целое алгебраическое неравенство.
Пример №255.
При всех натуральных значениях n решить неравенство
Решение:
Пусть 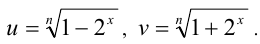 Тогда неравенство примет вид
Тогда неравенство примет вид 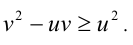 Поделим на
Поделим на 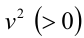 и обозначим
и обозначим 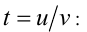
1) Если n — чётное, то 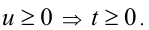 Поэтому
Поэтому
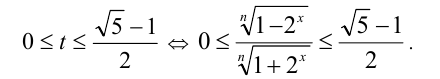
Возводя неравенство в n -ю степень, получим
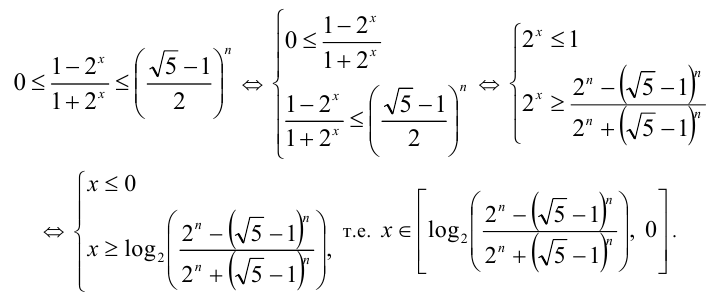
2) Если n — нечётное, то
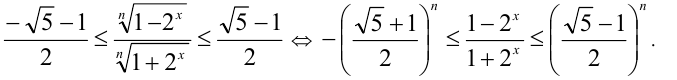
Решая это неравенство, получаем 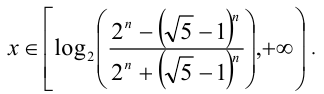
Осталось объединить полученные решения.
Смысл всех указанных выше подстановок состоит в том, что они позволяют рационализировать уравнение, избавить его от присутствия радикалов и, следовательно, тем самым сделать его проще для дальнейшего решения.
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:

