Замена переменных в кратном интеграле

Оглавление:

Замена переменных в кратном интеграле

Замена переменных в кратном интеграле. Во-первых, сохранить обозначения и предположения из предыдущего пункта. В частности, предположим, что Р-1-к-1 непрерывной дифференцируемой карте от открытого множества SJ, чтобы открыть набор C *и Якобиан не равно нулю на границе О.) открыт набор, Си. Ой, г * с. В соответствии с и Р карты, предположим, что множество Γ сопоставляется Γ.Затем Γ и Γстановятся компактными, внутренняя точка Γ перемещается внутрь, а граница Γ отображается на границу Γ. $ 46.Изменение нескольких интегральных параметров Сто семьдесят восемь Теорема 2 (формула для изменения переменных двойного интеграла).Определите функцию f (x, y) и продолжите с Γ.И затем… Доказательство.

Заметим, что интеграл (46.32)существует как Интеграл последовательных функций в замыкании квадратичной области. Людмила Фирмаль

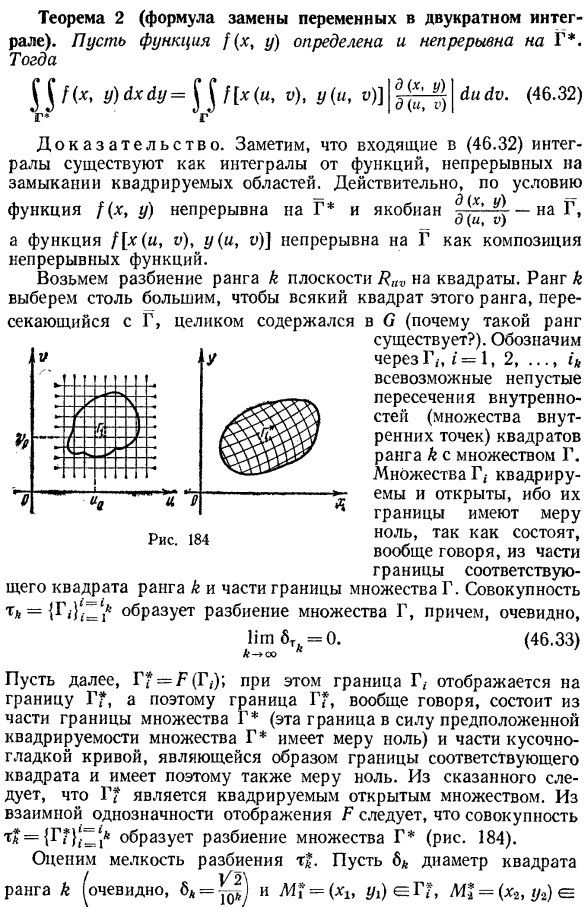
Действительно, по гипотезам Функция f (x, y) непрерывна с Γи Якобианом Д(х, г） Г д(U, V с)） Кроме того, функции f [x (u, y), y (u, y)] непрерывны на гамме как синтез непрерывных функций. Разделите ряды плоскости на квадраты. Выберите ранг, который настолько велик, что все квадраты, пересекающие этот ранг, полностью содержатся в O(такой ранг Существует ли она? это не. Yn / = 1, 2,…. 1к представлять через Непустое пересечение всех видов рангов K-квадратного интерьера (множество внутренних точек) и множества G. множество Γ является 2-м порядком и открыто. Потому что эти границы есть、 Вообще говоря, от части границы соответствующего квадрата ранга k и части границы множества G. коллекция mA = {Γ.}’!; * Сформировать разбиение множества гамма и выявить $ $ /( * .Г)AxAy = ^
） (46.33） Иш 8Т = 0.

Кроме того, пусть = T7 (T); Это получается из того, что сказано, что Γявляется открытым множеством 2-го порядка. От 1-к-1 отображение Р, установить τХ= {??} ^ = ’Образует разбиение множества* * (рис. 184). Оценим тонкость разбиения m|. 8 *с квадратным диаметром Ранг k (очевидно, 8 * = U) и M1 =(x1, d2) CEG), M1 =(x2, y2) e = 46.2.Обратите внимание на двойную интегральную переменную Сто семьдесят девять Следующий, мг (=гамма-и мг;; Р (ТХ)=-Ми Р (мм)= М присутствует, далее, Р (мм 42 42); 6А. Так… Р (М1-м |)=] / а(ХХ-ХС-У2) 2 ^ сотсби х)+(ОЦК; г), (46.34） Здесь ω (8; x) и ω (6; y) модуль непрерывности функций x = x (μ, σ) и V-V (u, V) на компактном множестве G.

Поскольку эти функции непрерывны с Γ, они равномерно непрерывны (см. и 19.6). Фри ко(6; х)= ТМ Колорадо (8 *; У)= 0.(46.35)） Ко * со Диаметр d (T [) (от 46.34) д(гг)= Зир Р(L4G, М |)К©2 (б; х)+ СО2 (6а; г)）、 м? = Т1 л. с. | э * И так оно и есть.、 БТ * = Зир с /(Т?) В ВР (8К; х) СО2(8А; г）、 г * ЭМ | Поэтому, благодаря (46.35) Золото bT * = 0 * K(46.36） К ^ Ш 4 Теперь выделим только те элементы разбиений xk и m\, где замыкание не пересекает границ gT и gTмножества Γ и Γ. MA (dG) и m соответственно!(ГЕНЕРАЛЬНЫЙ ДИРЕКТОР.)* та (ДГ)= {Т,. Γ-ээ ма, Γ, [} ДГ =φ}, ми(ДГ *)= {тг. ГГ € = т?, ГГПдГ * = ф}. Благодаря предположению, Ггет * (ДГ) существует только в случае г, ета (gt), В этом случае M(gt) состоит только из элементов T и E ta, которые являются целыми квадратами, содержащимися вместе с границами множества G.

Интегральная сумма функций f (x, y) o, m (Г.(См.§ 44.3), А e как точка (k, mp), (G) несколько вершин (, -, и соответствующий квадрат Γ, -). Б = х(У1,у), Р \ 1 = г(У, в). (46.37)） * Легко видеть, что равенство (46.36) непосредственно получено из равномерной непрерывности непрерывного отображения компактного множества (см. лемму 41.4 в§ 4). § 46.Замена переменных кратными интегралами Сто восемьдесят То есть рассмотрим сумму следующих форм: огр |(ЗР *)= 2 П (46.38） Джи? ЭМ /(АР *） Как известно (см. теорему условия 44.3 5), поскольку условия выполнены(46.36） г)Аю. (46.39） к-ко-п.

Так как в этом случае граница Γ отображается на границу Γ, вообще говоря, граница Γявляется частью границы множества Γ (эта граница измеряется предполагаемой перпендикулярностью множества Γ0), а так как она является частью демаркированной гладкой кривой и соответствующего квадрата, то существует также главный 0. Людмила Фирмаль

С другой стороны, для ГГ = к (г;), г; является квадратом, поэтому для γ это-et * (DG), следуя теореме 1 в предыдущем абзаце、 Р17 = | ^(U, о, -)! ч + эрг (46.40)） Где е = е (е на компакт-Γ (, в,, 6Т (6) стремится к нулю равномерно на 6-0.Если вы замените (46.37) и (46.40) на (46.38)、 БТ *(ДТ *)= 2 / [постоянного тока(а/, г;), г (у {, V с ^)] \ ^(у^, г.)| г; + * г, а * да + 2 е / [х(м -, ви), у (щ, Ц.)] {АГ-. (46.41） Гета(ag） Сумма этих сумм распространяется на все индексы I, где Γ не пересекает границу G. Для первой суммы в правой части уравнения (46.41), см. теорему 5 44.3, по условию(46.33). ） МН 2 / [*(, -, г»), г(и, Г ^)] \ ^(у^, г.)| * −00 (ДГ） =§$ / [*(а, в), г(У, В)] \ ^ {у, Z)| г Для 2-й суммы равенства (46.41) она стремится к нулю как k + co. In факт, функция.

Обобщенное интегральное неравенство Минковского.	Криволинейные координаты.
Геометрический смысл модуля якобиана в двумерном случае.	Замена переменных в n-кратном интеграле.