Оглавление:


Замена переменной
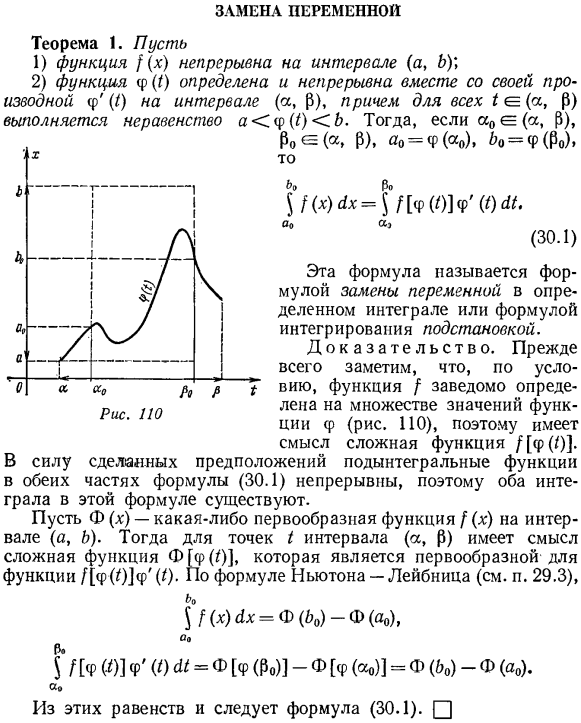
Замена переменной. Теорема 1.Фото: Joshua Roberts / PA 1) функция/(x) непрерывна на интервале (a, b) ’、 2) Функция φ(I) определена, ее производная Φ ’ ( / ) вместе с интервалом (a, P), неравенство a для всех^ e(a, P).。((). это отличный способ начать свой день. для a0e(a, P)、 По = Е(А, П), А0 =φ(А0), В0 =φ (По).И затем… \ 1 (x) yx = \ /[φ(0]φ ’(9 л. О, да. (30.1) Эта формула называется формулой подстановки переменных или интегральной формулой подстановки для конкретного интеграла. Доказательство. Прежде всего отметим, что, выдвигая гипотезу, функция I намеренно определяется для множества значений функции φ (рис.110).Поэтому комплексная функция/ [φ ( / )] имеет смысл.
Пусть Φ (x) примитивная функция f (x) интервала (a, b).Тогда для точки I интервала (a, P) имеет смысл комплексная функция Φ[Φ (0), являющаяся обратной производной функции ФΦ (0) Φ ’(0-Формула Ньютона-Лейбница (см.§ 29.3). 5 [(х) DX =Φ(В0) Φ(А0)、 П О0 $ / [φ(9) φ ’(0 м =Φ[po (по)]-Φ[ϕ]] =φΦ0) φ(А0). ССО Из этих равенств следует уравнение (ZOL). Я не уверен. Замена переменной золы Четыреста семьдесят пять Как видно из доказательства, формула (30.1) справедлива как для A0 Po, так и для a0 P0. Заметим, что некоторые значения функции φ ( / ) могут не принадлежать интервалу [a0, b0], где интегрирование происходит в левой части уравнения (ZOL) (см. Рисунок PO).
Из-за сделанных предположений подынтегральная функция с обеих сторон уравнения непрерывна, поэтому в этом уравнении присутствуют оба интеграла. Людмила Фирмаль
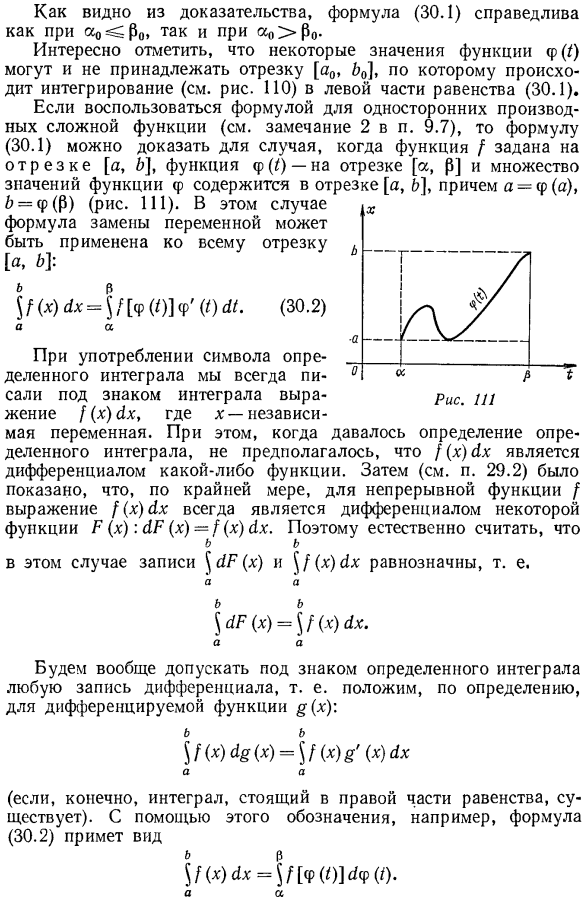
- Если формула используется для односторонней производной комплексной функции(см. 9.7 и примечание 2), то формула (30.1) может быть доказано, если функция/задана интервалу[a, b], функция φ ()) находится в интервале[a, P], а множество значений функций φ включено в интервал[a, b]и a =f(a), b = f(P) (рис.111). в этом случае выражение подстановки переменных может быть применено ко всему сегменту[a, b]. $ / = ( * ) Ж= $ / [Ф(0]ф ’(0и. Но、
При использовании знака конкретного интеграла всегда пишется Формула} (x) yx под знаком интеграла. Где X-независимая переменная. Кроме того, когда определялся определенный интеграл, не предполагалось, что F (x) xx является производной функции. Затем (см.§ 29.2) указано, что для непрерывной функции/по крайней мере, выражение {(x) xx всегда является производной функции P(x). р (х)= [(х) ух. Поэтому естественно предположить б, б. В этом случае ввод Но、 Б, б. ^ пп (х)= ^ /(х) ух.
- В общем случае предположим дифференциальную запись под знаком определенного интеграла. То есть, по определению, ставим дифференцируемую функцию e (x). (х) [(х) е(х)= \ [(х) г(х) ух Но、 (Конечно, если есть Интеграл на правой стороне равенства).Используя эту нотацию, например, выражение (30.2) принимает вид \ [{х) DX = ![(Р (0) полипропилен (0)Но、 476.§ 30.Уравнение подстановки переменных и интегрирования по компонентам Итак, определим переменную x =φ (I) б В Интеграле\ 1 (x) xx вы можете формально установить x в любом месте Но… Г (Г)и, соответственно, изменить пределы интеграции.
Обратите внимание, что применяя формулу (30.1) (30.2, соответственно), вы можете использовать ее как слева направо, так и справа налево, как в случае неопределенного интеграла. Людмила Фирмаль
- Однако в этом нет необходимости, поскольку, в отличие от неопределенного интеграла, который должен вернуться к исходной интегральной переменной в конце вычисления, цель здесь состоит в том, чтобы найти число, равное значению каждого рассматриваемого интеграла по доказанной формуле. Два Образцы. 1.Вычислите Интеграл$ e ^ xdx. Приложение О Получаем мула (30.1)справа налево(здесь роль переменной^играет x $ О 2.Предположим, вам нужно вычислить Интеграл^] / ex-1 dx. Священник О Упростите подынтегральное выражение, установив Uex-1 = I. То есть измените переменную x = 1n(1 + / 2). Потому что тогда это Лх ^ −2 и есть 0 ^ x ^ 1n2 1П 2 (К? 1 yx = 2 Один ■;) 11 = = 2 [1-ags1§;] o = Затем примените формулу (30.1) слева направо, чтобы.
Смотрите также:

