Оглавление:
Замечания к решению задач о равновесии системы сходящихся сил
При решении задач статики о равновесии несвободного твердого тела под действием системы сходящихся сил рекомендуется придерживаться следующего порядка.
- Выделить тело (узел, шарнир, стержень и т. п.), равновесие которого должно быть рассмотрено для определения неизвестных величин. Таким будет то тело, к которому приложены заданные и искомые силы или силы, равные по модулю искомым. Так, если требуется определить силу давления тела на связь, то можно рассмотреть равновесие тела, к которому приложена равная этой силе но модулю и противоположная ей по направлению реакция данной связи. Если заданные силы приложены к одному телу, а искомые к другому, связанному с ним, то приходится последовательно рассматривать равновесие каждого тела в отдельности. Как это делается, показывается в.
- Сделать ясный схематический чертеок и нанести на него активные силы, приложенные к телу, равновесие которого рассматривается.
- Освободить тело от наложенных на него связей, заменяя их действие на тело соответствующими реакциями связей. Нанести па чертеж реакции наложенных на тело связей. При определении их направлений нужно пользоваться соображениями, о которых говорилось ранее (§5).
- Для определения искомых величин можно пользоваться установленными условиями равновесия системы сходящихся сил как в геометрической, так и в аналитической форме.
Если пользуются геометрическим способом, то искомые силы или другие неизвестные в данной задаче величины определяют путем построения замкнутого силового многоугольника или чисто графически (что удобно только для плоской системы сходящихся сил), строя его в строго определенном масштабе или вычисляя его стороны и углы по правилам геометрии и тригонометрии.
Аналитическим способом можно пользоваться при любом числе сил (как плоской, так и пространственной системы). Искомые неизвестные мы находим при этом, составляя два уравнения равновесия (10) для плоской системы сходящихся сил и три уравнения равновесия (9) для пространственной системы сходящихся сил.
- При решении задачи аналитическим способом координатные оси следует располагать гак, чтобы проекции сил на эти оси находились наиболее просто. Часто бывает удобно одну из осей направить перпендикулярно какой-либо неизвестной силе.
Все расчеты при решении задач рекомендуется производить в общем виде, подставляя соответствующие числа лишь в окончательные результаты.
Первое время, до приобретения навыков в составлении уравнений равновесия, полезно значения проекций сил на координатные оси заносить в таблицу. Это облегчает проверку решения и отыскание возможной ошибки.
Пример задачи:
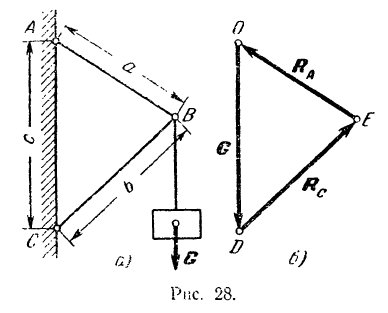
Стержни 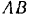 и
и 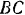 (рис. 28. о) соединены между собой и с вертикальной стеной посредством шарниров. Длина стержней:
(рис. 28. о) соединены между собой и с вертикальной стеной посредством шарниров. Длина стержней: 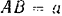 и
и 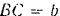 . Расстояние
. Расстояние 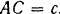 . Определить реакции стержней
. Определить реакции стержней 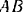 и
и 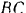 на шарнирный болт
на шарнирный болт 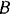 , если к нему подвешен груз весом
, если к нему подвешен груз весом 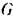 .
.
Решение:
Па шарнирный болт 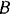 действуют силы: направленная вниз вертикальная сила
действуют силы: направленная вниз вертикальная сила 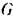 тяжести груза и реакции
тяжести груза и реакции 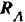 и
и 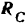 стержней
стержней 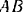 и
и 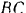 , направленные вдоль этих стержней. Так как точка
, направленные вдоль этих стержней. Так как точка 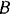 находится в равновесии под действием приложенной к ней системы сходящихся сил
находится в равновесии под действием приложенной к ней системы сходящихся сил 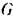 ,
, 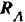 и
и 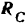 то построенный для этой системы силовой многоугольник должен быть замкнутым. Строим этот многоугольник (рис. 28,б). откладывая (в каком-либо масштабе) из произвольной точки
то построенный для этой системы силовой многоугольник должен быть замкнутым. Строим этот многоугольник (рис. 28,б). откладывая (в каком-либо масштабе) из произвольной точки 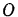 вектор
вектор 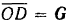 и проводя из его концов прямые
и проводя из его концов прямые 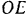 и
и 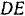 . параллельные искомым реакциям, т. е. параллельные стержням
. параллельные искомым реакциям, т. е. параллельные стержням 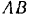 и
и 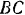 . Длины сторон
. Длины сторон 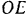 и
и 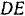 полученного силового треугольника дают в выбранном масштабе сил модули искомых реакций
полученного силового треугольника дают в выбранном масштабе сил модули искомых реакций 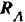 и
и 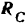 . Для того чтобы вычислить их, проще всего воспользоваться вытекающей из подобия треугольников
. Для того чтобы вычислить их, проще всего воспользоваться вытекающей из подобия треугольников 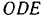 и
и 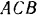 пропорциональностью их сторон:
пропорциональностью их сторон:
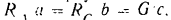
откуда
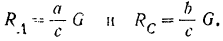
Пример задачи:
Стержень 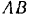 (рис. 29, а) прикреплен к вертикальной стене при помощи шарнира
(рис. 29, а) прикреплен к вертикальной стене при помощи шарнира  и удерживается под углом в 60 к стене при помощи веревки
и удерживается под углом в 60 к стене при помощи веревки 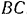 . образующей со стержнем также угол в 60. Определить величину и направление реакции шарнира, если известно, что вес стержня
. образующей со стержнем также угол в 60. Определить величину и направление реакции шарнира, если известно, что вес стержня  и приложен в его середине.
и приложен в его середине.
Решение:
Решим данную задачу аналитически. Треугольник  , как это ясно из чертежа, является равносторонним. Далее, так как линия действия силы тяжести
, как это ясно из чертежа, является равносторонним. Далее, так как линия действия силы тяжести 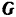 параллельна прямой
параллельна прямой 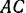 и делит сторону
и делит сторону 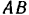 треугольника
треугольника 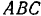 пополам, то она делит в точке
пополам, то она делит в точке 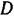 пополам и сторону
пополам и сторону 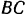 . Следовательно, проходящая через точку
. Следовательно, проходящая через точку 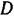 линия действия реакции
линия действия реакции 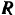 является для треугольника
является для треугольника 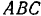 медианой и в то же время, по свойству всякого равнобедренного треугольника, высотой треугольника и биссектрисой
медианой и в то же время, по свойству всякого равнобедренного треугольника, высотой треугольника и биссектрисой 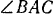 . Отсюда находим, что
. Отсюда находим, что 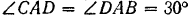 и
и 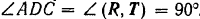 . Для определения величины реакции шарнира примем точку
. Для определения величины реакции шарнира примем точку 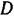 за начало координат и проведем координатные оси так, как показано на рис. 29, б. Проектируя все сходящиеся в точке
за начало координат и проведем координатные оси так, как показано на рис. 29, б. Проектируя все сходящиеся в точке 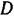 силы на ось
силы на ось 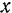 и составляя соответствующее уравнение равновесия, получим
и составляя соответствующее уравнение равновесия, получим
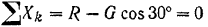
откуда
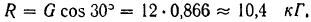
Проектируя силы на ось  , легко найти и натяжение веревки.
, легко найти и натяжение веревки.
Пример задачи:
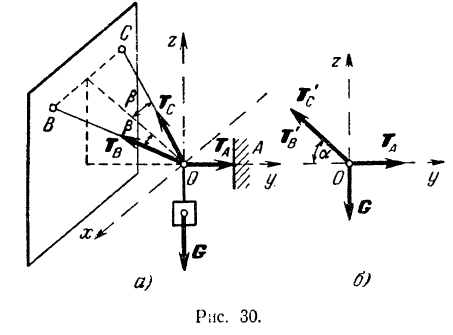
Груз 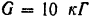 (рис. 30,а) удерживается в равновесии тремя веревками: горизонтальной
(рис. 30,а) удерживается в равновесии тремя веревками: горизонтальной 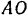 и двумя веревками
и двумя веревками 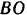 и
и 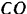 , плоскость которых наклонена к горизонтальной плоскости под углом
, плоскость которых наклонена к горизонтальной плоскости под углом 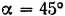 и перпендикулярна к вертикальной плоскости, проходящей через веревку
и перпендикулярна к вертикальной плоскости, проходящей через веревку 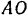 . Веревки
. Веревки 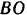 и
и 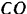 симметричны относительно этой вертикальной плоскости и образуют с нею угол
симметричны относительно этой вертикальной плоскости и образуют с нею угол 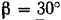 . Определить натяжение веревок.
. Определить натяжение веревок.
Решение:
В точке 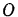 сходится пространственная система сил: сила
сходится пространственная система сил: сила 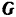 тяжести груза и реакции
тяжести груза и реакции 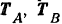 и
и 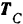 веревок
веревок 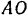 ,
, 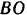 и
и 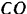 . Выбираем оси координат так, как показано на рис. 30, а, совместив плоскость
. Выбираем оси координат так, как показано на рис. 30, а, совместив плоскость 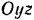 с вертикальной плоскостью симметрии.
с вертикальной плоскостью симметрии.
Проекции сил 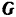 и
и 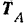 на координатные оси находятся просто. При проектировании же сил
на координатные оси находятся просто. При проектировании же сил 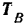 и
и 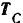 на оси
на оси 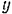 и
и 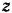 воспользуемся приемом двойного проектирования. Найдем сначала проекции
воспользуемся приемом двойного проектирования. Найдем сначала проекции 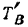 и
и 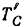 сил
сил 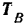 и
и 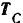 на плоскость
на плоскость 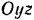 , а затем уже найденные проекции этих сил на плоскость будем проектировать на оси
, а затем уже найденные проекции этих сил на плоскость будем проектировать на оси 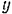 и
и 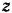 (рис, 30,6).
(рис, 30,6).
Очевидно, что модули проекции сил 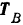 и
и 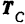 на плоскость
на плоскость 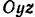 будут
будут 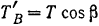 и
и 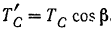 . Теперь находим проекции всех сил на координатные оси.
. Теперь находим проекции всех сил на координатные оси.

Составляем уравнения равновесия:
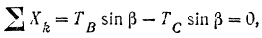
откуда
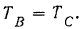
Об атом можно было догадаться и сразу из соображении симметрии
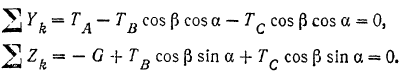
Решая эти уравнения и подставляя числовые данные, находим:
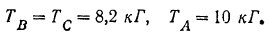
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Теоретическая механика — задачи с решением и примерами
Возможно вам будут полезны эти дополнительные темы:

