Оглавление:
Замечания к решению задач о равновесии плоской системы сил
Методика решения задач о равновесии системы сил, расположенных как угодно на плоскости, та же, что и для сходящихся сил. В дополнение к сказанному в § 12 можно лишь рекомендовать за центр моментов выбирать точку, лежащую на линии действия одной из неизвестных сил (еще лучше — точку пересечения линий действия двух неизвестных сил, если только положение этой точки легко определяется). Момент этой силы относительно таким образом выбранного центра будет равен нулю, и эта неизвестная сила исключится из уравнения моментов.
Все аксиомы и положения статики устанавливаются для так называемых сосредоточенных сил, т. е. для сил, приложенных к тем или иным точкам твердого тела. На практике же часто приходится иметь дело с силами, распределенными вдоль данной поверхности по некоторому закону. При решении задач статики такую систему сил надо заменить ее равнодействующей.
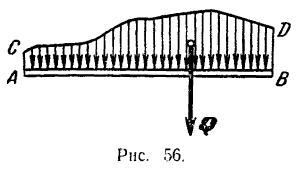
В случае плоской системы сил закон их распределения изображается при помощи кривой нагрузки (рис. 56). Ординаты этой кривой представляют собой так называемую интенсивность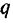 
нагрузки, т. е. модуль силы, приходящейся на единицу длины нагруженного бруса. Интенсивность измеряется обычно в кГ/м или н/м. Равнодействующая 
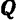всей нагрузки, расположенной на части бруса 
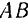, равна по модулю площади фигуры 
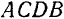(рис. 56), измеренной в соответствующем масштабе, и проходит через центр тяжести этой площади.
Большинство задач статики, как мы уже знаем, заключается в определении реакций связей, в частности, в определении реакций опор различного рода балочных систем, ферм и т. п.
Помимо шарнирных опор, подвижных и неподвижных, о которых говорилось ранее (§ 7), в практике
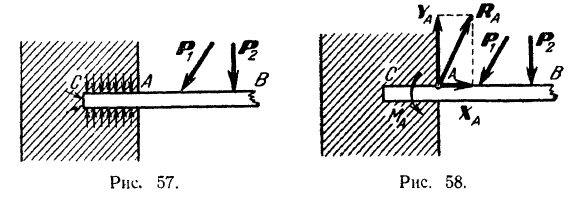
встречается еще и опора, осуществляемая жесткой заделкой (неподвижным защемлением) конца балки (рис. 57). Такая опора не допускает не только линейных перемещений балки (как и шарнирно-неподвижная опора), но и ее поворота. На заделанную часть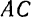 
балки действуют со стороны поверхностей, на которые она опирается, неравномерно распределенные силы (рис. 57).
Пользуясь теоремой о параллельном переносе силы, эти реакции можно привести к одной точке (рис. 58) и заменить одной силой — реакцией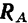 
приложенной в точке 
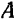и равной главному вектору распределенных реакций, и одной парой с моментом 
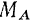, равным главному моменту этих сил относительно точки 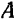. Нахождение неизвестной по модулю и по направлению реакции 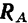, в свою очередь, можно заменить нахождением алгебраических значений 
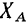и 
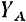двух составляющих этой силы.
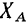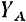Следовательно, нахождение реакции жесткой заделки сводится (см. задачу 12) в общем случае сил, расположенных как угодно на плоскости, к определению трех неизвестных величин: составляющих и реакции 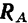, препятствующих любому линейному перемещению балки в плоскости действия сил, и алгебраической величины момента 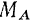реакций, препятствующего вращению балки под действием приложенных к ней активных сил.
Пример задачи:
Однородный стержень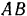 
длиной З м весом
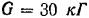опирается концом 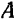на гладкий горизонтальный пол под углом 
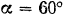и в точках 
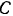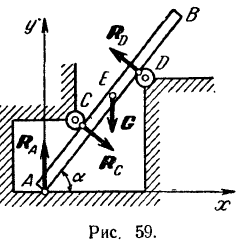
и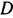 
на два ролика (рис. 59). Определить давление стержня на пол и ролики, если
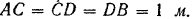
Решение:
Давления стержня на пол и ролики равны по модулю соответствующим реакциям пола и роликов. Реакция гладкого пола 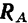перпендикулярна к полу. Реакции роликов 
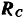и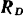 
, если пренебречь малым в них трением, перпендикулярны к поверхности стержня. Отбрасывая связи (опоры 
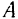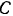, и 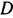) и заменяя их соответствующими реакциями, можно рассматривать стержень как свободный, находящийся в равновесии под действием сил 
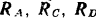и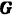 
(силы тяжести, приложенной в его середине — точке 
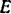), расположенных в одной плоскости. Проведя координатные оси 
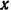и 
так,
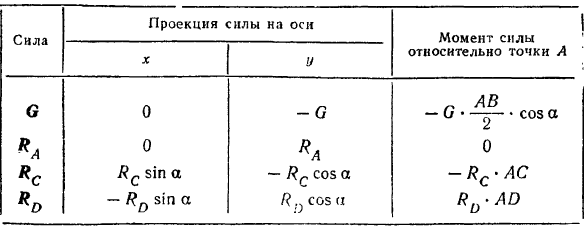
как показано на чертеже, и приняв за центр моментов точку , составляем таблицу проекций всех сил на выбранные координатные оси и алгебраических величин их моментов относительно точки . Уравнении равновесия (26) принимают вид
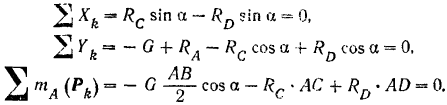
Из первых двух уравнений находим
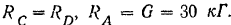
Решая последнее уравнение и подставляя значения
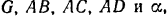
находим
Пример задачи:
Консольная балка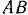 
нагружена так, как показано на рис. 60. Интенсивность равномерно распределенной нагрузки 
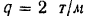. Длина балки 
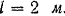В точке 
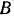балки приложена
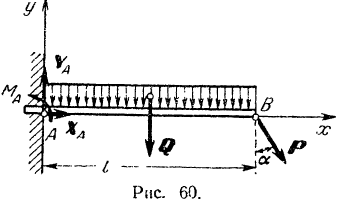
сосредоточенная нагрузка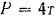 
, направленная вниз под углом 
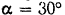к вертикали. Определить реакции жесткой заделки, пренебрегая собственным весом балки.
Решение:
Рассматриваем равновесие балки. Активными силами, приложенными к балке, будут: равномерно распределенная нагрузка, равнодействующая которой
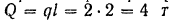
и приложена в середине балки, и сосредоточенная сила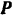 
. В точке 
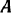на балку наложена жесткая связь (заделка в стену), препятствующая линейным перемещениям балки и лишающая ее возможности поворачиваться вокруг точки 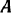. Действие такой связи, как говорилось выше (стр. 85), эквивалентно действию одной реакции 
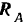и некоторой пары с моментом 
.
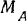Направление вращения этой пары нам, вообще говоря, пока неизвестно. Примем момент 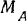этой пары за положительный, т. е. будем считать, что она стремится повернуть балку против хода стрелки часов. Если при решении задачи значение этого момента окажется отрицательным, то это будет означать, что в действительности направление вращения пары противоположно предположенному.
Так как направление реакции 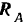нам также, вообще говоря, неизвестно, то разложим ее на составляющие 
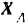и 
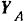, направленные так, как показано на рисунке.
Таким образом, балка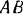 
находится в равновесии под действием плоской системы сил
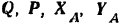
и пары с моментом 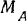. Составляем уравнения равновесия балки:
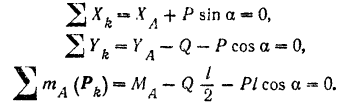
Решая эти уравнения и подставляя данные, получим:
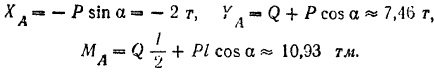
Отрицательное значение, полученное для показывает, что в действительности эта составляющая реакции заделки направлена в сторону, противоположную предположенной.
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Теоретическая механика — задачи с решением и примерами
Возможно вам будут полезны эти дополнительные темы:
