Оглавление:
Законы Кулона
Силой трения скольжения называется сила сопротивления скольжению одного тела по поверхности другого, возникающая в плоскости соприкосновения этих тел.
Основной причиной трения скольжения является то, что поверхности соприкасающихся тел не идеально гладки, а более или менее шероховаты. Вследствие этого при перемещении одного тела по поверхности другого требуется некоторая сила для преодоления микроскопических неровностей этих поверхностей. Приложение силы необходимо и для преодоления молекулярного взаимодействия между частицами поверхностных слоев соприкасающихся тел. Сила трения в той или иной степени возникает между всякими реальными поверхностями, сколь бы гладки они не были, и в значительной мере зависит от физических свойств этих тел. Поэтому учение о трении выходит за рамки теоретической механики, и если в ее курсе обычно все же рассматриваются элементы этого учения, то это делается лишь для того, чтобы уже при изучении курса теоретической механики иметь возможность применить ее положения к решению и таких практических задач, в которых нельзя пренебречь трением.
Вследствие крайней сложности этого физико-механического явления и трудности оценки многочисленных факторов, на него влияющих, на практике все еще продолжают пользоваться эмпирическими законами, установленными в конце XVIII века (1781 г.) французским ученым Ш. Кулоном (1736—1806), хотя они и представляют собой лишь грубое приближение к действительности.
Для уяснения этих законов проделаем на простейшем приборе (трибометре) следующий опыт.
Положим на неподвижную горизонтальную плоскость брусок весом 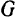 и будем действовать на него горизонтальной силой
и будем действовать на него горизонтальной силой 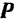 , для чего привяжем к телу нить (возможно ближе к основанию, чтобы уменьшить опрокидывающий момент) и, перекинув ее через блок, подвесим к ее концу чашку с гирями (рис. 68). До тех пор пока модуль силы
, для чего привяжем к телу нить (возможно ближе к основанию, чтобы уменьшить опрокидывающий момент) и, перекинув ее через блок, подвесим к ее концу чашку с гирями (рис. 68). До тех пор пока модуль силы 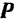 не достигнет некоторого значения, вполне определенного для данной пары соприкасающихся поверхностей и данного давления между ними значения, брусок будет оставаться в покое. Это свидетельствует о том, что, кроме нормальной реакции
не достигнет некоторого значения, вполне определенного для данной пары соприкасающихся поверхностей и данного давления между ними значения, брусок будет оставаться в покое. Это свидетельствует о том, что, кроме нормальной реакции 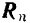 плоскости, равной по модулю и противоположной по направлению силе
плоскости, равной по модулю и противоположной по направлению силе 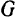 тяжести бруска, на него со стороны плоскости будет действовать еще и другая реакция
тяжести бруска, на него со стороны плоскости будет действовать еще и другая реакция 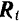 равная по модулю и противоположная по направлению горизонтальной силе
равная по модулю и противоположная по направлению горизонтальной силе 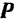 . Эта лежащая в касательной плоскости реакция
. Эта лежащая в касательной плоскости реакция 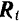 и есть, очевидно, сила трения, возникающая между поверхностью бруска и опорной плоскостью. Подобно тому как с увеличением веса
и есть, очевидно, сила трения, возникающая между поверхностью бруска и опорной плоскостью. Подобно тому как с увеличением веса 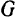 бруска будет увеличиваться модуль
бруска будет увеличиваться модуль 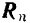 нормальной реакции плоскости, так и с увеличением модуля силы
нормальной реакции плоскости, так и с увеличением модуля силы 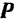 до некоторого предела, до тех пор пока брусок будет оставаться в равновесии, увеличивается и модуль
до некоторого предела, до тех пор пока брусок будет оставаться в равновесии, увеличивается и модуль 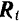 силы трения. Максимального своего значения эта сила достигает в тот момент, когда брусок под действием некоторого значения силы
силы трения. Максимального своего значения эта сила достигает в тот момент, когда брусок под действием некоторого значения силы 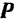 начнет двигаться.
начнет двигаться.
Сила трения, проявляющаяся при относительном покое тела, называется трением покоя, сила трения, действующая при скольжении тела, называется трением движения.
На основании многочисленных опытов Кулон установил следующие (приближенные) законы.
- Сила трения при прочих равных условиях не зависит от размера трущихся поверхностей.
Так, если в предыдущем опыте взять брусок, сделанный в форме параллелепипеда, имеющего грани одинаковой шероховатости, но неодинаковой площади, то модуль силы  , которую надо приложить к бруску для приведения его в движение, не будет зависеть от того, на какую грань мы поставим брусок. Нужно заметить, что этот закон приближенно справедлив лишь до некоторой величины удельного давления, т. е. давления, приходящегося на единицу площади трущихся поверхностей. Так, если поставить брусок на ребро, то сила трения будет значительно больше.
, которую надо приложить к бруску для приведения его в движение, не будет зависеть от того, на какую грань мы поставим брусок. Нужно заметить, что этот закон приближенно справедлив лишь до некоторой величины удельного давления, т. е. давления, приходящегося на единицу площади трущихся поверхностей. Так, если поставить брусок на ребро, то сила трения будет значительно больше.
- Величина силы трения покоя зависит от приложенных сил и до некоторого предела всегда такова, что предотвращает скольжение тел друг по другу. Однако она не может быть больше некоторого, вполне определенного для каждой данной пары трущихся поверхностей, максимального значения.
- Максимальная величина силы трения прямо пропорциональна силе нормального давления одного тела на другое.
Под силой нормального давления понимается сила давления, направленная по нормали к поверхности скольжения. Сила нормального давления равна весу тела только в том случае, если поверхностью скольжения является горизонтальная плоскость и на тело никаких других сил, кроме силы его тяжести, не действует.
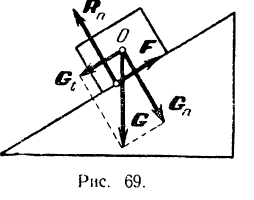
Если тело лежит на наклонной плоскости (рис. 69), то на величину силы трения влияет уже не его вес 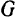 , а лишь составляющая
, а лишь составляющая 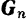 силы тяжести, перпендикулярная к плоскости и равная по модулю ее нормальной реакции
силы тяжести, перпендикулярная к плоскости и равная по модулю ее нормальной реакции 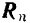 .
.
Если на тело, кроме его силы тяжести, действуют еще и другие силы, то под силой нормального давления тела на поверхность надо понимать нормальную составляющую равнодействующей всех приложенных к нему сил, которая равна по модулю нормальной реакции 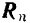 поверхности скольжения.
поверхности скольжения.
- Максимальная величина силы трения зависит как от материала и состояния трущихся поверхностей, так и от наличия и рода смазки между ними. Так, трение металла по металлу меньше трения дерева по дереву, трение между сталью и бронзой меньше трения стали по стали и т. д. Трение тел тем меньше, чем глаже трущиеся поверхности, поэтому поверхности соприкосновения трущихся частей машин обычно шлифуются. Смазывание трущихся поверхностей весьма сильно уменьшает трение. Смазка заполняет собой все неровности трущихся поверхностей и располагается тонким слоем между ними, так что непосредственное трение поверхностей заменяется скольжением их по смазывающей жидкости и скольжением друг относительно друга отдельных слоев этой жидкости.
Если обозначить через 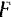 максимальную величину
максимальную величину 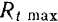 силы трения покоя, а через
силы трения покоя, а через 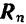 — нормальную реакцию опорной поверхности, то на основании данного закона будем иметь:
— нормальную реакцию опорной поверхности, то на основании данного закона будем иметь:
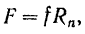
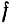 — коэффициент пропорциональности, называемый коэффициентом трения скольжения при покое.
— коэффициент пропорциональности, называемый коэффициентом трения скольжения при покое.
Из равенства 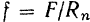 следует, что коэффициент трения скольжения есть число отвлеченное.
следует, что коэффициент трения скольжения есть число отвлеченное.
- Сила трения при движении меньше максимального значения силы трения покоя.
Опыт показывает, что для того чтобы вывести тело из состояния покоя, нужно при прочих равных условиях преодолеть большую силу трения, чем при движении тела.
Позднейшие опыты показали, что сила трения в движении зависит от скорости движения одного тела относительно другого и в большинстве случаев убывает с увеличением этой скорости, стремясь к некоторому пределу.
Величину силы трения при движении можно определить по формуле, аналогичной формуле (31), подставляя в нее вместо 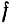 — коэффициента трения покоя
— коэффициента трения покоя 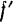 — коэффициент трения при движении.
— коэффициент трения при движении.
Ориентировочные средние значения коэффициентов трения (как в покое, так и при движении) для различных материалов и различного их состояния можно найти во всех технических справочниках, причем при грубых подсчетах часто не делают различия между коэффициентами трения покоя и при движении и пользуются во всех случаях значением коэффициента трения при движении. В расчетах же, требующих большой точности, силу трения приходится определять из опыта для каждой данной пары трущихся поверхностей и конкретных условий трения.
Пример задачи:
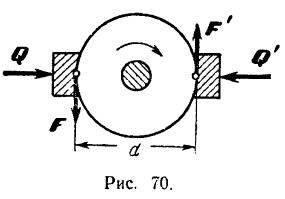
К валу (рис. 70) приложена пара с моментом 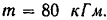 валу заклинено тормозное колесо, диаметр которого равен
валу заклинено тормозное колесо, диаметр которого равен 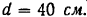 Определить коэффициент трения покоя между колесом и колодками, если колодки прижимаются к колесу силами
Определить коэффициент трения покоя между колесом и колодками, если колодки прижимаются к колесу силами
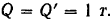
Решение:
Для того чтобы колесо оставалось в покое, необходимо. чтобы момент  приложенной к валу пары уравновешивался моментом пары
приложенной к валу пары уравновешивался моментом пары 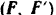 сил трения между колесом и колодками. Условием равновесия колеса, следовательно, является равенство
сил трения между колесом и колодками. Условием равновесия колеса, следовательно, является равенство
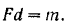
Максимальная величина силы трения покоя между колесом и колодками
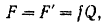
где 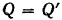 — силы нормального давления колодок на колесо. Подставляя значение силы
— силы нормального давления колодок на колесо. Подставляя значение силы 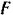 в первое равенство, будем иметь
в первое равенство, будем иметь 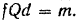 Отсюда
Отсюда
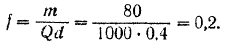
Пример задачи:
На дощатом деревянном пастиле (рис. 71), образующем с горизонтом угол 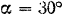 , находится груз весом
, находится груз весом 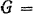
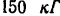 , заключенный в деревянный ящик. Определить модуль
, заключенный в деревянный ящик. Определить модуль
горизонтальной силы 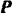 из условия, что груз находится в равновесии на наклонной плоскости. Коэффициент трения
из условия, что груз находится в равновесии на наклонной плоскости. Коэффициент трения 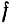 принять равным 0,3.
принять равным 0,3.
Решение:
Определим сначала 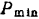 — минимальное значение модуля силы
— минимальное значение модуля силы 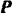 , необходимое для того, чтобы тело не скользило вниз по плоскости. Сила трения будет направлена в сторону, противоположную возможному движению, т. е. вверх по плоскости.
, необходимое для того, чтобы тело не скользило вниз по плоскости. Сила трения будет направлена в сторону, противоположную возможному движению, т. е. вверх по плоскости.
Таким образом, тело находится в равновесии под действием активных сил 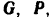 , силы трения
, силы трения 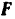 и нормальной реакции
и нормальной реакции 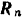 (рис. 71).
(рис. 71).
Проектируя все силы на оси 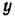 и
и 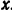 , направленные так, как показано на рис. 71, будем иметь:
, направленные так, как показано на рис. 71, будем иметь:
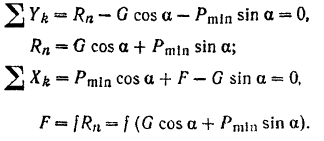
Подставляя это значение в предыдущее равенство, получим
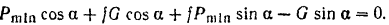
Решая это уравнение относительно 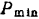 и подставляя числовые значения, найдем
и подставляя числовые значения, найдем
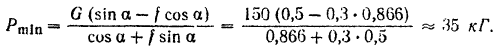
Если модуль силы 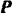 будет меньше
будет меньше 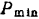 то тело начнет скользить вниз. Но если мы будем увеличивать модуль силы
то тело начнет скользить вниз. Но если мы будем увеличивать модуль силы 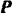 , то до некоторого предельного значения
, то до некоторого предельного значения 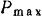 модуля этой силы равновесие тела на плоскости будет еще сохраняться, так как сила
модуля этой силы равновесие тела на плоскости будет еще сохраняться, так как сила 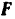 трения в этом случае будет уже направлена по плоскости вниз (сила трения всегда направлена в сторону, противоположную возможному движению). Уравнения равновесия останутся прежними, только знак перед проекцией силы
трения в этом случае будет уже направлена по плоскости вниз (сила трения всегда направлена в сторону, противоположную возможному движению). Уравнения равновесия останутся прежними, только знак перед проекцией силы 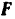 па ось
па ось 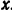 изменится на противоположный, и мы будем иметь
изменится на противоположный, и мы будем иметь
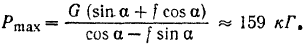
Соединяя теперь оба полученных решения, видим, что груз будет оставаться на наклонной плоскости в равновесии при всех значениях модуля силы 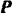 , заключенных в пределах
, заключенных в пределах 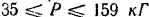 . При
. При 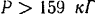 груз будет подниматься по плоскости, если же
груз будет подниматься по плоскости, если же 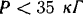 — опускаться.
— опускаться.
Необходимо заметить, что вообше условия равновесия тел при наличии трения выражаются неравенствами, а потому задачи на равновесие таких тел имеют не одно, а множество решений. Определенное решение получается лишь в тех случаях, когда рассматриваются предельные случаи равновесия, т. е. случаи, когда тело находится уже на границе между относительным покоем и движением или когда тело находится в движении.
Пример задачи:
Валы прокатного стана (рис. 72, а) вращаются в противоположные стороны и втягивают прокатываемый лист вследствие трения между ними и листом. Каково должно быть расстояние а между валами для того, чтобы на стане можно было прокатать листы толщиной 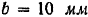 ? Радиус валов
? Радиус валов 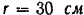 , а коэффициент трения для раскаленного железа и чугунных валов
, а коэффициент трения для раскаленного железа и чугунных валов 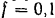 .
.
Решение:
К листу приложены следующие силы: нормальные реакции валов 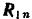 и
и 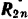 . направленные по радиусам
. направленные по радиусам 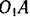 и
и 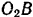 , и силы трения
, и силы трения 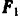 и
и 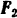 , направленные по касательным в точках
, направленные по касательным в точках 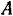 и
и 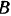 . В силу симметрии
. В силу симметрии 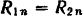 , а следовательно, равны по модулю и силы трения
, а следовательно, равны по модулю и силы трения 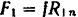 и
и 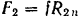 . Положим в дальнейшем
. Положим в дальнейшем 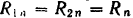 и
и 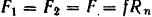 . Нормальная реакция
. Нормальная реакция 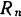 каждого вала разлагается (рис. 72, б) на вертикальную составляющую
каждого вала разлагается (рис. 72, б) на вертикальную составляющую 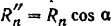 и горизонтальную
и горизонтальную 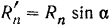 . Аналогично разлагаются и силы трения
. Аналогично разлагаются и силы трения
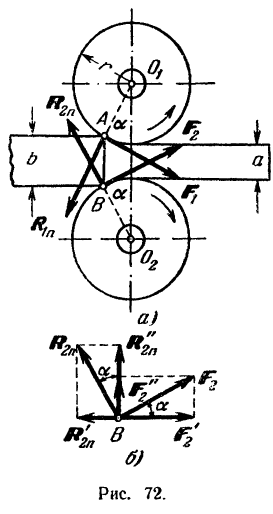
на горизонтальную составляющую
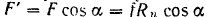
и вертикальную
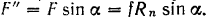
Для возможности втягивания листа и процесса прокатки необходимо, очевидно, чтобы сумма горизонтальных составляющих сил трения была не меньше суммы соответствующих составляющих нормальных реакций валов, т. е. чтобы имело место неравенство
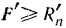
или
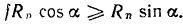
Отсюда
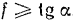
Выразим 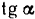 через заданные размеры и толщину листа. Из рис. 72, а имеем:
через заданные размеры и толщину листа. Из рис. 72, а имеем:
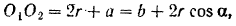
откуда
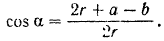
Выражая 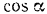 через
через 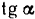 и заменяя последний величиной
и заменяя последний величиной 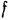 , будем иметь:
, будем иметь:
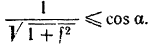
Подставляя это значение в предыдущее равенство, найдем:
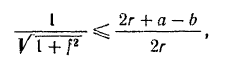
откуда и определяется искомое расстояние между валами
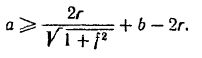
Подставляя числовые значения, получим
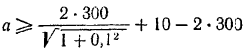
или
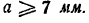
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Теоретическая механика — задачи с решением и примерами
Возможно вам будут полезны эти дополнительные темы:

