Оглавление:






Законы распределения случайных величин
- Закон распределения случайных величин По закону распределения случайных величин Понять наиболее распространенные характеристики, уникальное связывание больших групп Случайная переменная Закон раскрывает природу этих связей.
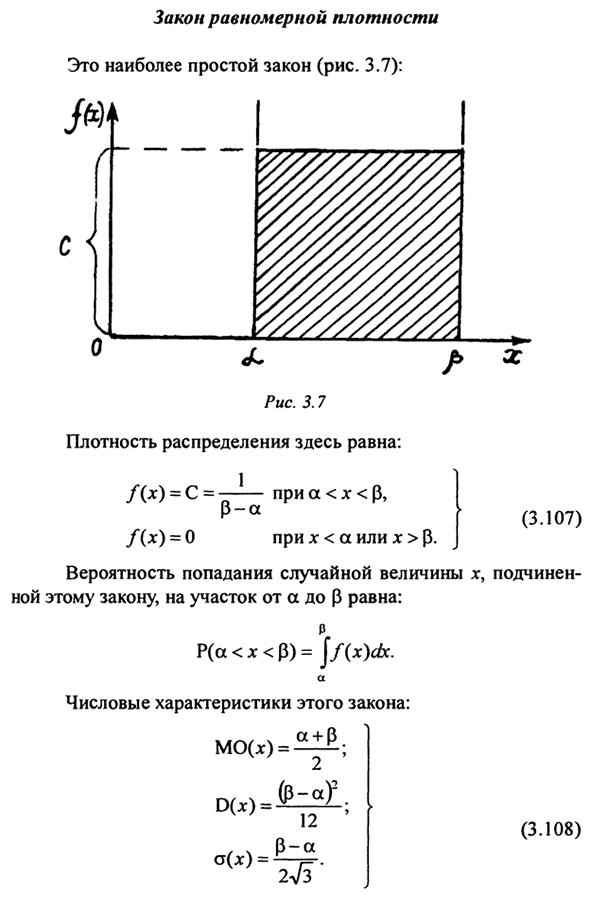
- В актуальной задаче, прежде всего Сталкиваются с тремя основными законами: -Запад равномерной плотности; Закон Пуассона. Нормальный закон. Закон равномерной плотности Это самый простой закон (рис. 3.7): Рисунок 3.7 Плотность распределения здесь следующая. I ) = c = — 1 Если α <χ <β, β-α Для j (<α или χ> β) f (x) = 0. (3,107) Вероятность попадания в случайную величину χ.
Подчиненный этому закону сечение от α до β равно: P (a <χ ) = - J = e ^. Людмила Фирмаль
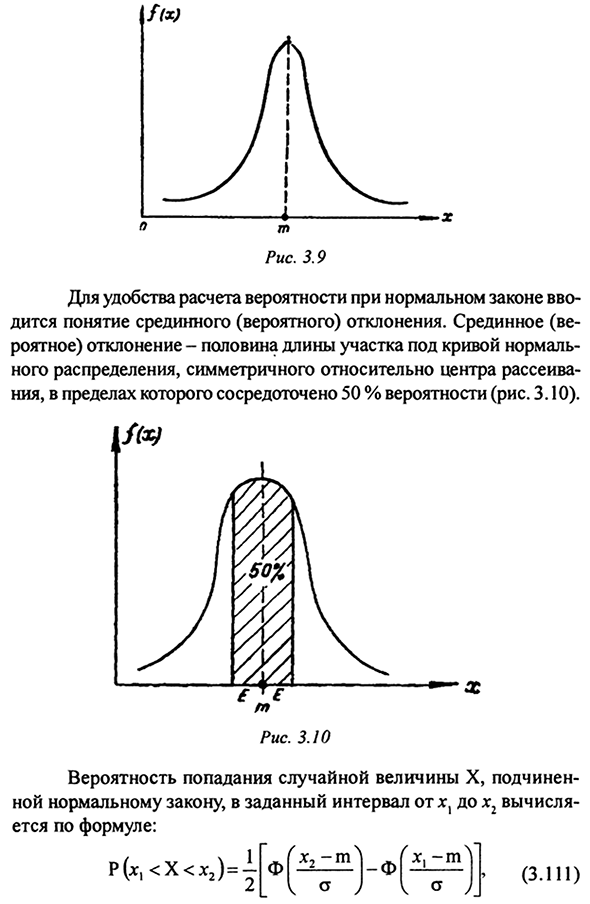
Рассчитать вероятность по нормальному закону Представлено понятие срединного (расчетного) отклонения. медиана (Расчетное) Отклонение — половина длины сечения под кривой Нормальное распределение, симметричное относительно центра Дисперсия с вероятностью 50% (рис. 3.10). Вероятность попадания случайной величины X.
- Следуйте нормальному закону с заданными интервалами от хх до хг Рассчитывается по формуле: P (x1 <X <x2) = ~ F м -Φ χ. -m (3,111) Где ° W = «7r ^, т.е. 2dt (3,112) (Ф (х) — функция Лапласа, см. Таблицу 3.31), ХТ т = σ Следует также отметить, что функция (3.112) нечетна. Так что для отрицательных аргументов, знак должен быть изменен Функция, т. Е. Φ (−x) = — P (x). 140 Часть I.
Глава 3 если m = 0, то есть центр дисперсии совпадает с началом Опорная ось х тогда 1 P (x, <X <x2) = — G * σ (3,113) Если m = 0 и указанный интервал от начала Опорная симметрия, т.е. ах = — /, ах- /, то P (x, <X <x2) = Φ 1’P Чау (3,114) Пример 3.32 Обеспечить высокое качество материалов и технологий Отклонения в размерах железобетонных деталей от внутренних норм Стандартное отклонение σ = ± 3 мм. Вероятность фактических частей (P) / = ± 1,5 мм отличается от стандарта?
Решения Следуйте формуле (3.114), используя таблицу. Найдите 3.31: 3 P (x1Людмила Фирмаль
Смотрите также:
| Случайные величины и их характеристика | Теория массового обслуживания (теория очередей). Метод Монте-Карло |
| Числовые характеристики случайных величин | Теории игр и статистических решений |

