Законы композиции

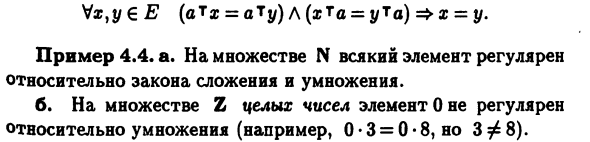
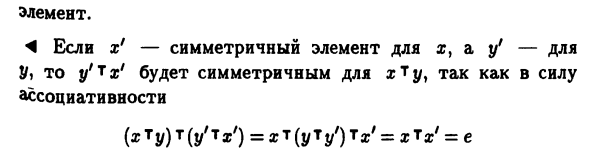
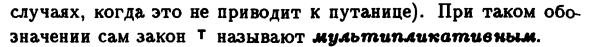
Законы композиции

• На практике набор обычно Элементы, которые могут выполнять определенные операции, Или, как говорится, внутренний закон установлен Конфигурация. Определение 4.1. Установите E, внутри Для каждых двух, двоичный закон построения т Элементы a и E связаны с элементом c ‘€ E. Называется состав этих элементов, обозначенный c-a ^ ​​b. Другими словами, внутреннее биноминальное правило композиции M на множестве E называется отображением множества ExE В E Пример 4.1 а. На множестве R действительных чисел Сложение и умножение являются внутренними двоичными файлами Закон синтеза обозначен а + 6 и а-б соответственно (Умножение также обозначается как a x b или просто ab). б.

# Полезные законы — это те законы. Композиция с конкретными характеристиками. Определение 4.2. Композиция биномиального метода В примере 4.2 множество E называется ассоциацией. а. На множестве N натуральных чисел Сложение и умножение являются ассоциативными законами Конфигурация. б. Поднять до целого числа с тем же набором N В общем случае положительная степень не ассоциативна. Так, например, (23) 4 = 84 = 212 и 2 * = 281. Замечания 4.1. Если закон ассоциативный, Руководство определяет окончательный состав последовательности элемент … Tan = ta, — или Tflj, J- {1, 2, …, n}.

Некоторое подмножество P (Y) из всех подмножеств Биномиальный закон композиции имеет операции Союз и пересечение. Людмила Фирмаль

Определение 4.3. Композиция биномиального метода Множество E называется коммутативным Пример 4.3 а. Добавьте и умножьте с набором N Это коммутативный закон. б. В том же наборе сила Поскольку это общий случай, коммутативный закон а б ба. Определение 4.4. Элемент E называется регулярным По поводу закона = aTy) l (xta = yTa) = »s = y Пример 4.4 а. В множестве N все элементы регулярны По поводу закона сложения и умножения. б. В множестве целых чисел Z элемент 0 не является регулярным Относительно умножения (например, 0 • 3 = 0 • 8, но примечание 4.2. Из-за регулярности элементов,

Вырубить его Например, выражение case a ^ x = a ^ y Регулярность элемента a можно записать в виде x = y. Различают левую регулярность, если a * x = aTu можно уменьшить Если x ^ a = y ^ a также подразумевается, регулярность на a и регулярность справа х = у, очевидно, элемент а является регулярным относительно Только если закон м регулярен справа и слева В то же время Определение 4.5. Нейтральный элемент По отношению к биномиальному правилу составного m множества E Следующие элементы называются e € E Уже € E xTe = e «Tx = x.

• Если такой элемент существует, это единственный элемент. Конечно, есть два нейтральных Этот элемент ». Тогда e = e’Te = eTe ‘= e’. Нейтральные элементы правильные. Пример 4.5 а. На множестве R действительных чисел 0-нейтральный элемент для сложения. 1 По поводу умножения. б. Установите P (E) для всех подмножеств множества E Пустое множество является нейтральным элементом Для Союза базовый набор E относительно Последующее пересечение 0UA = A \ J0 = A, APE = EPA = A Определение 4.6. Биноминальное правило в м Задано для установки E с нейтральным элементом e. Симметричен элементу x e E (иногда говорят: обратный, Противоположность) называется элементом x’e E x ^ x ‘= x’Tx = e. В этом случае х называется симметризацией Расходные материалы.

Пример 4.6. а. б. При умножении на набор Q рациональных чисел Если симметрично относительно x, Φ0 равно 1 / x. # Для набора E с нейтральными элементами E относится к внутреннему биному композиции t Следующие две теоремы верны. Теорема 4.1. Берит -Ассоциативный метод- Элементы, которые могут быть симметричны, неизбежно регулярны По отношению к m он имеет единственный симметричный элемент.

Симметричный на множестве R Если добавлено, несколько чисел х будут одинаковыми С противоположным знаком. Людмила Фирмаль

Предположим, что есть два в 4 набора E Симметрично относительно х элементов х1 и х «, то Определения 4.2, 4.5 и 4.6, x1 = x’te = x’t (xx «) = {x ‘ Другими словами, единственный элемент, симметричный относительно x, это. Для обоснования регулярности симметризуемых элементов Предположим, что x x * a = xTb. тогда Затем используйте свойство подключения m, чтобы получить = (X’Tx) Tb или, согласно определениям 4.6 и 4.5, e ^ a = et & и a = 6, т.е. по определению 4.4 элемент x является регулярным

Относительно т. »> Теорема 4.2. Если m является законом ассоциации, а W является у Элементы, которые могут быть симметризованы, и x «Tu также могут быть симметризованы Пункт. 4 Когда x1 является симметричным элементом i, а y1 является i Для Y y’thx симметричен относительно xty. Связь и Соответствует определению 4.6. ► Определение 4.7. Положите два комплекта на E Внутренняя бинарная конструкция т и К они говорят m является дистрибутивным по отношению к in в случае Vx, y, z € E. и Пример 4.7. а. Умножьте с множеством Z

Распределительно по отношению к сложению, т.е. и б. В том же наборе Z добавление не производится Распределительный по умножению с. Установите P (E) для всех подмножеств множества E В зависимости от характеристик этих операций, соединяется с пересечениями Раздайте друг другу. Замечание 4.3. В определении 4.7 Поговорим о первых отношениях, а затем о дистрибутивности Относительно а, только правая сторона, удовлетворяется только вторая По поводу распределения м только на левой стороне. такие как Устанавливает силу N для умножения Распределить только вправо: (xy) r = x * yy} где rf \ и

Определение 4.8. f c e Под белой полосой подмножества множества E композиция любых двух элементов F Если это принадлежит F, F E закон т или считается устойчивым Подмножество множества E относительно закона m. В этом случае в подмножестве F индуцированный по методу f внутренний метод Композиция тф. Пример 4.8 а. Четный набор Закрытое подмножество для сложения и умножения Да, натуральное число установлено N. б. Набор E *, обычный элемент множества E Оснащен методом ассоциации Для m, если два элемента множества регулярны,

Я регулярно сочиняю музыку. с. Set Etm Set Симметричный элемент E, с законом ассоциации m, стабильный qthoch- Это закон. Определение 4.9. Оборудовано с набором F Если есть закон, оснащенный набор множествоF F закон Ти. так что m> соответствует закону. По закону Установите F, закон m # будет расширен до Я Закон m> определяется F, или они говорят, что F встроен Я. Там не так много законов состава Приносит видимые практические выгоды. наиболее Общее сложение и умножение Форма записи.

В дополнительной форме легальной записи Состав двух элементов a и 6 равен c = a + b, нейтрален Элемент (если это не вызывает путаницы) Часто отображается как 0, симметрично относительно Указывает -a. При использовании такого для композиции метода м В обозначениях m обычно называют законом сложения Состав. В мультипликативной форме закон Положение элемента c = a * b (или c = ab), обозначено нейтральным ny и симметричные элементы соответственно 1 и «1 (эти Если это не приводит к путанице). здесь По замыслу сам закон m называется мультипликативным.

Смотрите также:

Предмет математика

Основные элементарные функции	Основные алгебраические структуры
Некоторые элементарные функции	Группа подстановок