Закон сохранения количества движения системы
Из уравнения (160) предыдущего параграфа следует, что если
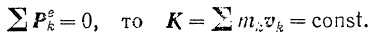
Пели в течение некоторого времени главный вектор всех внешних сил, действующих на систему, равен нулю, то количество движения системы все это время остается постоянным.
Из уравнений (161) того же параграфа следует, что если
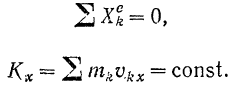
Если в течение некоторого времени сумма проекций на какую-либо ось всех внешних сил, действующих на систему, остается равной нулю, то проекция на ту же ось количества движения системы все это время остается постоянной.
Из уравнений (163) и (164), выражающих весьма важный закон сохранения количества движения системы, следует, что при отсутствии внешних сил внутренние силы системы не могут изменить ее общего количества движения. Не влияя на общее количество движения всей системы, внутренние силы могут, конечно, вызывать изменение количества движения отдельных точек {или тел) системы. При этом, согласно закону равенства действия и противодействия, ускорения двух взаимодействующих точек системы по модулю обратно пропорциональны их массам и противоположны по па-правлению.
Так, например, если рассматривать орудие и снаряд как одну систему, то давление пороховых газов при выстреле будет внутренней силой. Давление газов, сообщая некоторое количество движения снаряду, одновременно сообщает такое же количество движения, направленное в противоположную сторону, орудию. Это вызывает явление так называемой отдачи (отката) орудия, если, конечно, оно не укреплено неподвижно, т. е. если нет внешнего противодействия такому откату.
Явлением «отдачи» объясняется и ускоренное движение ракеты. Продукты сгорания выбрасываются с большой скоростью из хвостовой части ракеты назад. Так как силы давления газов являются для данной системы (ракета — продукты сгорания) внутренними силами, то они не могут изменить общего количества движения этой системы и потому ракета получает соответствующее количество движения, направленное в противоположную сторону — вперед.
Так как ракета (пли реактивный самолет) получает ускорение в результате отбрасывания назад продуктов сгорания, вырабатываемых в самой ракете, то ее ускоренное движение одинаково возможно как в воздухе, так и в безвоздушном пространстве. Однако, подобное движение самолета с винтовым движителем, осуществляемое в результате отбрасывания воздушным винтом назад с некоторой скоростью определенной массы воздуха, в безвоздушном пространстве невозможно.
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Теоретическая механика — задачи с решением и примерами
Возможно вам будут полезны эти дополнительные темы:

