Оглавление:
Закон сохранения кинетического момента системы
Из уравнения (178) находим, что при
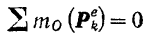
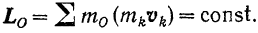
Если главный момент всех внешних сил, действующих на систему, относительно какого-либо центра в течение некоторого времени равен нулю, то ее кинетический момент относительно этого центра все это время будет постоянным (как по модулю, так и по направлению).
Как это следует из формулы (179), если
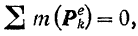
то
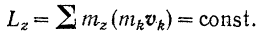
Если в течение некоторого времени главный момент всех внешних сил, действующих на систему, относительно какой-либо неподвижной оси остается равным нулю, то кинетический момент системы относительно этой оси все это время будет постоянным.
Равенство нулю главного момента внешних сил относительно некоторой оси имеет место, в частности, при отсутствии внешних сил или когда все они параллельны данной оси или ее пересекают.
Из закона сохранения кинетического момента следует, что при отсутствии eneiuHux сил внутренние силы системы не могут изменять ее кинетический момент, так же как не могут изменять и общее количество движения системы.
Закон сохранения кинетического момента системы хорошо иллюстрируется опытом на так называемой «скамейке» Н. Е. Жуковского. Она представляет собой горизонтальную платформу, вращающуюся вокруг вертикальной оси на шариковых подшипниках (для умень» шения третгая).
Если человек с гирями в руках встанет на платформу (рис. 197, а), то внешними силами, действующими на систему (платформа — человек), будут: сила тяжести платформы и человека с гирями и нормальная реакция пола, параллельные вертикальной оси вращения, и реакции подшипников, пересекающие эту ось. Таким образом, сумма моментов всех внешних сил, действующих на данную систему, относительно оси вращения системы будет равна нулю. Но в этом случае кинетический момент вращающейся системы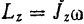 
относительно оси ее вращения должен оставаться на основании закона сохранения постоянным
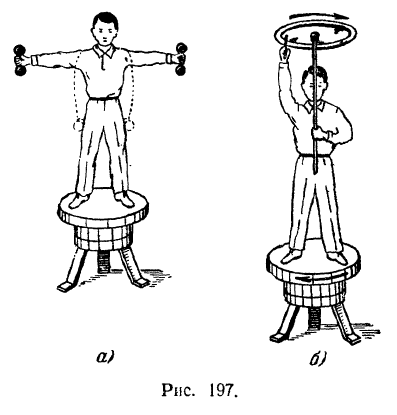
Если извне привести платформу во вращение, то человек может изменять ее угловую скорость, изменяя распределение масс и тем самым изменяя момент инерции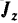 
системы относительно оси ее вращения. Вращение системы заметно ускоряется, если человек будет приближать руки (с гирями) к груди и, наоборот, замедляется, если он будет удалять гири от оси вращения.
Подобным способом увеличения угловой скорости тела путем уменьшения его момента инерции относительно оси вращения тела широко пользуются танцоры и акробаты.
Если человек, стоящий на неподвижной платформе скамейки Жуковского, поднимет над головой велосипедное колесо (рис. 197,6) и приведет его во вращение вокруг вертикальной оси, то он сам, вместе с платформой, начнет вращаться в противоположную сторону. Угловая скорость платформы будет при этом такой, чтобы кинетический момент
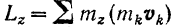
всей системы (платформа — человек — колесо) оставался равным нулю.
Силы давления пороховых газов для системы ствол орудия — снаряд являются внутренними силами и не могут изменить кинетического момента этой системы, который до выстрела был равен нулю. Вследствие наличия нарезов в стволе орудия снаряду при выстреле сообщается, помимо поступательного движения, еще и вращательное движение вокруг его оси. Если бы не было внешних сил (реакций цапф, которыми ствол закреплен в лафете орудия), то кинетический момент системы должен был бы оставаться равным нулю и ствол орудия начал бы вращаться в сторону, противоположную вращению снаряда. Цапфы препятствуют этому вращению и поэтому испытывают при выстреле дополнительное давление.
С помощью теоремы об изменении кинетического момента системы удобно решать задачи на вращательное движение системы или системы, состоящей из тел вращающихся и тел, совершающих поступательное и плоское движение.
Если главный момент всех действующих на систему внешних сил относительно оси вращения равен нулю и, следовательно, имеет место закон сохранения кинетического момента, то можно найти зависимость между угловой скоростью системы и скоростями отдельных ее частей.
Пример задачи:
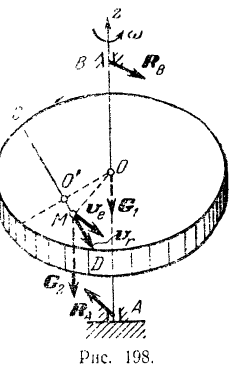
Круглая горизонтальная платформа (рис. 198) может вращаться без трения вокруг вертикальной оси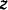 
, проходящей через центр 
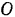платформы. По хорде 
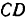, перпендикулярной к радиусу платформы, движется человек по закону:
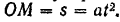
В начальный момент платформа вместе с человеком находилась в покое. Вес платформы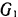 
ее радиус 
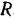, вес человека 
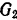. Расстояние
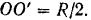
Найти угловую скорость вращения платформы в момент времени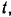 
приняв платформу за сплошной диск и человека за материальную точку.
Решение:
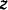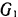Для того чтобы исключить неизвестную силу трения между подошвами ног человека и платформой, включаем в систему платформу вместо с находящимся на ней человеком. Действующие па эту систему внешние силы либо параллельны оси (силы и 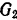тяжести платформы и человека), либо пересекают эту ось (реакции 
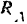подпятника и 
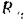подшипника), Следовательно, главный момент всех внешних сил воздействующих на данную систему относительно ее оси вращения:
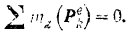
Отсюда кинетический момент системы относительно оси 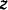, по закону его сохранения, должен оставаться постоянным. Так как в начальный момент система находилась в покое, то кинетический момент системы относительно оси ее вращения:
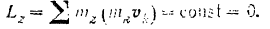
Кинетический момент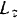 
системы относительно оси 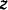складывается из кинетического момента 
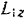платформы и кинетического момента 
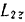человека относительно той же оси.
Предположим, что платформа при движении человека будет вращаться против хода стрелки часов с угловой скоростью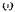 
. Тогда по формуле (177) кинетический момент платформы
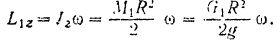
Человек участвует в двух движениях: относительном по хорде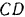 
со скоростью
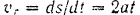
и переносом вместе с платформой со скоростью
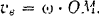
Его кинетический момент относительно оси 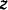будет равен
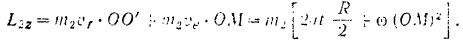
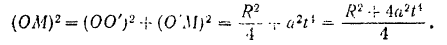
Подставляя это значение в предыдущее выражение, будем иметь:
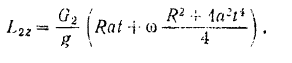
Тогда кинетический момент всей системы будет равен
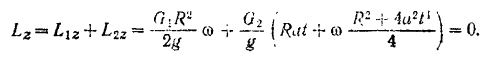
Отсюда находим
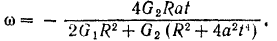
Знак минус показывает, что платформа будет вращаться в направлении, противоположном предположенному, т. е. по ходу стрелки часов.
Пример задачи:
Груз весом 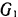скользя вниз по наклонной плоскости, приводит во вращение барабан весом 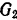посредством намотанной на барабан нити (рис. 199). Барабан, представляющий собой сплошной цилиндр радиуса 
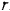вращается вокруг горизонтальной оси 
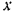(перпендикулярной к плоскости чертежа). Коэффициент
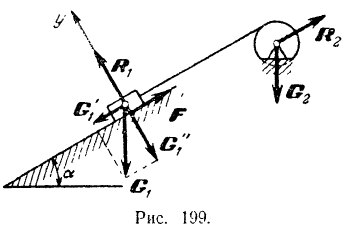
трения тела о наклонную плоскость —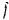 
. Угол наклона плоскости к горизонту — 
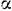. Пренебрегая массой нити и ее трением о барабан, определить его угловое ускорение.
Решение:
Для того чтобы исключить неизвестную реакцию веревки, принимаем груз и барабан за одну систему.
Разложим силу 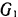тяжести груза па две составляющие 
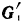— направленную вдоль нити и по модулю равную
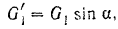
и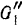 
— направленную перпендикулярно к плоскости скольжения груза и равную по модулю нормальной реакции 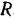плоскости. Составив дифференциальное уравнение движения центра масс груза в проекции на ось 
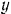(рис. 199), будем иметь:
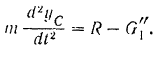
Так как
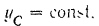
то
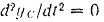
и, следовательно
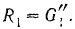
Силы 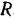и 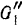взаимно уравновешиваются и потому можно считать, что внешними силами, действующими на рассматриваемую систему, будут только: составляющая 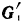силы тяжести груза, сила 
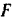трения груза о плоскость (модуль которой 
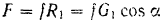), сила 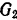тяжести барабана и сила 
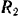реакции оси барабана. Так как последние две силы пересекают ось 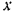вращения барабана, то главный момент всех действующих на систему внешних сил относительно оси 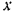будет равен
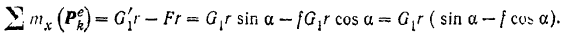
Кинетический момент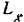 
системы относительно оси 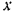будет складываться из кинетического момента 
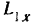груза и кинетического 
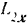момента барабана.
Рассматривая поступательно движущийся груз как материальную точку и принимая оо внимание, что скорость груза равна скорости точки на окружности барабана, будем иметь:
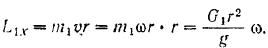
Кинетический момент барабана относительно оси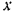
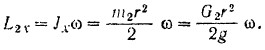
Кинетический момент всей системы
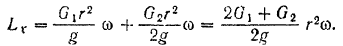
По теореме об изменении кинетического момента системы имеем:
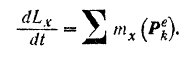
Подставляя в это уравнение найденные значения
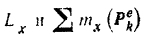
получаем:
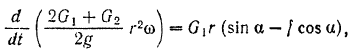
откуда находим искомое угловое ускорение барабана;
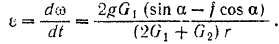
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Теоретическая механика — задачи с решением и примерами
Возможно вам будут полезны эти дополнительные темы:
