Оглавление:





Закон распределения нормальных и касательных напряжений в сечении стержня
- Закон распределения. И напряжение сдвига в поперечном сечении Из стержня Рассмотрим базовую область, назначенную окрестности любой точки M срединной грани (рис. 344). Предположим, что отсутствует взаимное давление между продольными волокнами при ограниченном кручении, а также при изгибе и свободном кручении. Исходя из этого предположения, получаем по закону крюка4-ei’y (x)]
yr=0. (13.22) Г Р Р Имея в виду, что 403 функция 6″и i’O (x) не зависят от arc5, выражение (13.22) можно записать так:—EY»y oz DR+EY (x) DR-0. RG (13.23) Отсюда найдите нужную функцию и'»(Х)= — Интеграл (13.24), который содержится в числителе, является геометрической характеристикой поперечного сечения стержня.
По аналогии со статическим моментом территории, он обозначается 5 Вт и Людмила Фирмаль
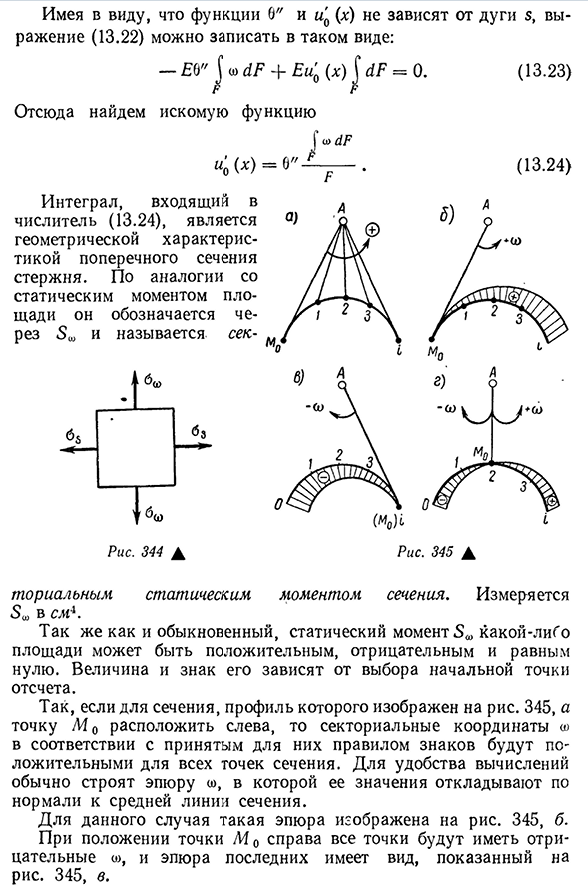
называется сек- (13.24) Рис 344 рисунок. 345A Сечение торического статического момента. Измеряется 5 Вт в СМ*. Как и в обычном случае, статические моменты в любой области равны положительному, отрицательному и нулю. Его размер и знак зависят от выбора начальной точки. Поэтому, если профиль является сечением, которое показано на рисунке. 345, а точка М0 расположена слева, и секторные координаты со В соответствии с правилами знака для них будут
положительными для всех точек поперечного сечения. Для удобства расчета постройте график ОЗ, значение которого обычно успешно откладывается на среднюю линию разреза. В данном случае такой сюжет показан на рисунке. 345, род. В положении точки M o справа все точки имеют отрицательное значение W, а последний график
- имеет вид, показанный на рисунке. 345, ст. Если 404 точка m o находится в любом промежуточном положении, то график (o) будет выглядеть так:двузначные цифры(рис. 345, г). Из соображений этих графиков следует, что 5C0 всего сечения при соответствующем выборе положения точки m o может быть равно нулю. Давайте договоримся выбрать точку M0 в будущем. ^1г=0. (13.25)Е. А из равенства (13.24) оно и^s)=0, и нормальное напряжение приняло такой вид: Ош= — EV»I.
(13.26) это выражение выражает закон распределения. Так как Е и 6″в определенном сечении постоянны, то участок всегда будет иметь форму, подобную участку Ю. Точка M0 называется главной векторной нулевой точкой. Из уравнения (13.26) следует, что если 6 ‘является постоянной величиной, то, например, при свободном кручении 6″=0, то нормальное напряжение в этом случае также не возникнет. Для определения тангенциального напряжения в поперечном сечении стержня мы поступаем так же, как и при выводе формулы
Журавского (Глава VIII, глава 67). 405 из-за этого вырезают два поперечных элемента yx и стержень и отрезают часть крепления, от которой(фиг. Людмила Фирмаль
346). На АТ и А стороны этой детали, предположим, действует нормальное напряжение, и в этом отношении тангенциальное напряжение возникает в продольном сечении ТТГ, равномерно распределенном по толщине 8. Напряжение TS, действующее на продольное сечение рассматриваемой отрезной детали, считается положительным, если оно направлено в противоположном направлении к оси X. В плоскости отсечной части, которая находится в плоскости поперечного сечения стержня, тангенциальное напряжение возникает по закону четности. Внешние кромки элементов A-A{и B, yx, считаются свободными от напряжений. Мы используем состояние равновесия attsch^части и нулевую сумму
проекций всех сил на ось x:2x=y oshs1g-b M x+Y+^ — YH^yr=0, C z27) ^ЗТ^ЗТ Где мы находимся * Гда=Ле. (13.28)) п отн Подставляя значение (13.26), после уменьшения на yx, Y—(- E»I) yr. (13.29)) Г отн Если вы дифференцируете выражения в скобках Под интегралом, и W не зависит от x, то E’ » O = — — — — Я а) год. (13.30) ЕТС Интегрирование правой части уравнения (13.30) представляет собой статический момент в сечениях отсечной части сечения, т. е. 5°to = ^(oal(13.31) Я ем История * Ихъ выносится за знак у tegral, потому что интеграция осуществляется на РГ. 406that метод, наконец, найти =—(13.32) Уравнение (13.32)представляет закон распределения напряжений в поперечном сечении стержня. Так как множитель E'»для конкретного участка является постоянной величиной、, 5 0ts Изменения в законодательстве. Следует также отметить, что 5°TC (13.32) в Формуле может быть принято как для любых отрезных частей, то есть секционных частей TA и th. Эта ситуация подчиняется условиям раздела 5Ш=0 в целом.
Смотрите также:

