Оглавление:


Закон Гука для главных осей
- Закон крюка главной оси. Теперь перейдем к установлению зависимости между напряжением и упругой деформацией в сложном
напряженном состоянии. Ограничимся рассмотрением Изотропных веществ, как и прежде,
для растяжения и сжатия. Рассмотрим Людмила Фирмаль
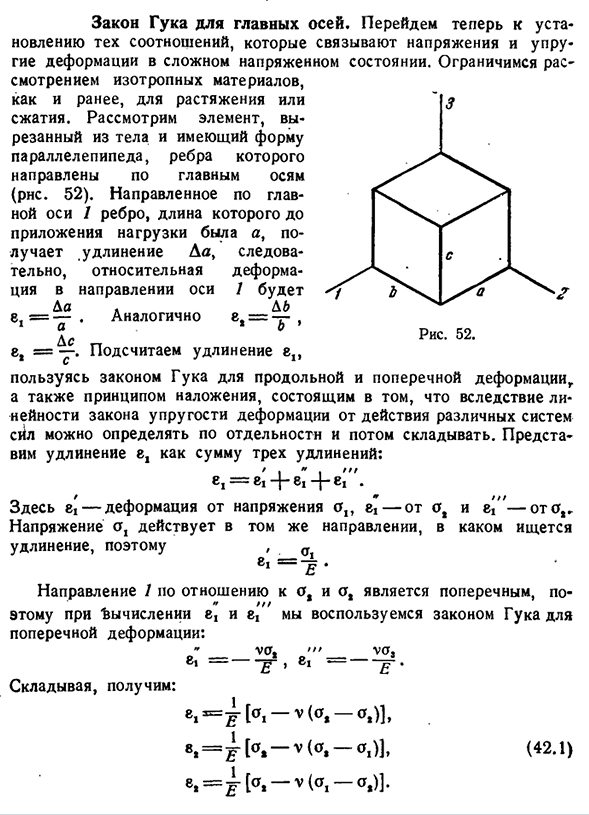
элементы, которые вырезаны из корпуса и имеют форму параллелепипеда. 52). Вдоль главной оси направления / края, его длина была перед нагрузкой и локальным tive, что в e > =T e,
мы вычисляем удлинение 8t, продольное и поперечное удлинение деформации e представим как сумму трех удлинений: где et-ET-деформация от напряжения от a и e/ ’ — около TA2. Поскольку
- напряжение a действует в том же направлении, что и то, в котором ищется удлинение, a8*=i — В отношении направления 1.И a является поперечным, поэтому при расчете et и et мы используем закон крюка
для Восемьдесят один Складывая, получаем: 8! = ^ — И-v (o,-0.)], 8. =^[о’. — в(0, — 0i)], е=^[0, — в(©! — ©.)]. у<Т «Е’ Вот именно. — F ’ 8 1 (42.1) 38 сложных напряженных состояний[Глава III
поперечной деформации: Людмила Фирмаль
Последние две формулы написаны по аналогии, приобретая их точно таким же образом, как и первая. Формула (42.1)представляет закон крюка для пространственного напряженного состояния.
Смотрите также:
| Главные касательные напряжения | Полный расчет балок на прочность |
| Октаэдрическое напряжение | Концентрация напряжений при изгибе |

