Заказать теоретическую механику — решение на заказ онлайн

Здравствуйте! Я Людмила Анатольевна Фирмаль, занимаюсь помощью студентам более 17 лет. У меня своя команда грамотных, сильных преподавателей. Мы справимся с любой поставленной перед нами работой технического и гуманитарного плана. И неважно – она по объёму на две формулы или огромная, сложно структурированная, на 125 страниц! Нам по силам всё, поэтому не стесняйтесь, присылайте.

Если что-то непонятно — вы всегда можете написать мне в WhatsApp и я вам помогу!

Как заказать выполнение заданий по теоретической механике

Вы можете написать сообщение в WhatsApp. После этого я оценю ваш заказ и укажу стоимость и срок выполнения вашей работы. Если условия Вас устроят, Вы оплатите, и преподаватель, который ответственен за вашу работу, начнёт выполнение и в согласованный срок или, возможно, раньше срока Вы получите файл готовой работы в личные сообщения.

Сколько может стоить заказ

Стоимость заказа зависит от задания и требований Вашего учебного заведения. На цену влияют: сложность, количество заданий и срок выполнения. Поэтому для оценки стоимости заказа максимально качественно сфотографируйте или пришлите файл задания, при необходимости, загружайте поясняющие фотографии лекций, файлы методичек, указывайте свой вариант.

Какой срок выполнения заказа

Минимальный срок выполнения заказа составляет 2-4 дня, но помните, срочные задания оцениваются дороже.

Как оплатить заказ

Сначала пришлите задание, я оценю, после вышлю вам форму оплаты, в которой можно оплатить с баланса мобильного телефона, картой Visa и MasterCard, apple pay, google pay.

Гарантии и исправление ошибок

В течение 1 года с момента получения Вами готового решения заказа действует гарантия. В течении 1 года я и моя команда исправим любые ошибки в заказе.

Чуть ниже я предоставила темы по теоретической механике, по которым смогу вам помочь + добавила в них теорию, чтобы вы смогли прочитать и если у вас есть свободное время сами попытались решить, но если нет времени вы сможете заказать у меня.

Статика

Основные понятия и аксиомы статики

К оглавлению…

Статика — это раздел теоретической механики, где рассматриваются вопросы сложения сил и условия покоя тел под действием сил. Абсолютно твердое тело — это тело, расстояния между точками которого не изменяются. В теоретической механике рассматриваются (если не оговорено особо) только абсолютно твердые тела. Поэтому для сокращения можно вместо этого употреблять термины «тело» или «твердое тело», имея в виду абсолютно твердое тело.

Сила — это вектор, являющийся мерой механического взаимодействия тел. Система сил — это совокупность сил, приложенных к твердому телу. Система сил называется уравновешенной если под ее воздействием твердое тело находится в покое.

Две системы сил называются эквивалентными если состояние тела не изменяется в случае замены одной системы на другую. Если система сил эквивалентна одной силе, то эта сила называется равнодействующей данной системы сил.

Если две системы сил, объединенные вместе образуют уравновешенную систему сил, то они называются уравновешивающими по отношению друг к другу.

Аксиомы статики. Аксиома 1. Твердое тело под действием двух сил находится в равновесии тогда и только тогда, когда силы равны по модулю и направлены в противоположные стороны по общей линии действия (рис. 1).

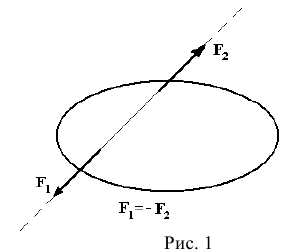
Аксиома 2. Состояние тела не изменится если к действующей на него системе сил прибавить или отнять от нее уравновешенную систему сил. Следствие из аксиом 1,2. Силу, действующую на твердое тело, можно не изменяя состояния тела переносить параллельно себе вдоль линии действия силы в любую точку тела.

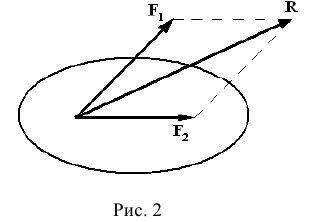
Аксиома 3 (аксиома параллелограмма). Две силы, приложенные к твердому телу в одной точке, имеют равнодействующую, приложенную в этой же точке и являющейся диагональю параллелограмма, построенного на векторах сил как на сторонах (рис. 2).

Аксиома 4 (аксиома равенства действия и противодействия).Силы взаимодействия двух тел всегда равны по модулю и противоположно направлены по одной прямой (рис.3).

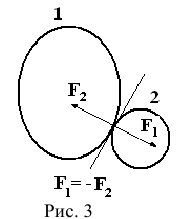
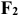Силы и приложены к разным тела, поэтому говорить о уравновешивании этих сил бессмысленно.

Аксиома 5 (аксиома отвердевания). Если нетвердое тело находится в равновесии (в покое), то равновесие не нарушится если тело отвердеет. Эта аксиома позволяет использовать условия равновесия твердого тела для нетвердых тел ( жидкостей, газов, деформируемых тел), которые изучаются в других дисциплинах. Следует только заметить, что данные условия равновесия для нетвердых тел являются только необходимыми, но не всегда достаточными.

Тело называется свободным, если его перемещение в пространстве не ограничено другими телами, в противном случае тело называется несвободным.

Тела, ограничивающие перемещение данного тела называются связями ( по отношению к данному телу).

Сила с которой связь действует на данное тело называется реакцией связи. Аксиома 6 (аксиома освобождаемости от связей). Любое несвободное тело можно считать свободным, если связи его мысленно отбросить и заменить их действие реакциями связей. Эта аксиома имеет важное значение при решении задач, так как условия равновесия твердого тела в статике выведены в основном для абсолютно свободных твердых тел.

Возможно эта страница вам будет полезна:

Предмет теоретическая механика

Основные типы связей и их реакции

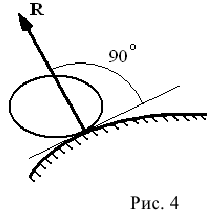
Гладкая опорная поверхность. Если твердое тело опирается на идеально гладкую (без трения) поверхность, то реакция поверхности R направлена по нормали к ней в точке соприкосновения, т. е. перпендикулярно к касательной плоскости в данной точке поверхности (рис 4). Такая реакция называется нормальной реакцией.

• Гибкая нить. (Рис. 5)

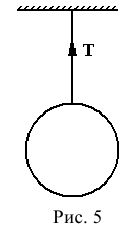
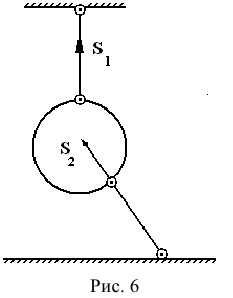
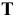— сила натяжения нити, которая направлена вдоль нити и всегда от тела, равновесие которого будет рассматриваться. 3. Прямолинейный стержень, закрепленный шарнирно. (Рис. 6)

и — реакции стержней, стержень 1 растягивается, стержень 2 сжимается.

Цилиндрический шарнир (подшипник). Цилиндрическим шарниром называется совокупность неподвижного валика и надетой на него втулки , соединенной с твердым телом (рис.7 ). При этом твердое тело может поворачиваться вокруг оси валика. Направление реакции неподвижного цилиндрического шарнира А сразу указать нельзя, поэтому при решении задач реакция шарнира заменяется двумя взаимно перпендикулярными составляющими и 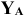. 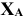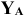Определив в ходе решения задачи и можно найти модуль и направление реакции шарнира. Реакцию шарнира можно разложить на составляющие по любым двум направлениям.

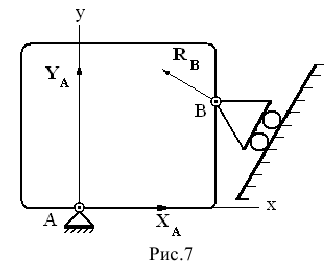
Если цилиндрический шарнир подвижный (рис. 7шарнир В), то он не противодействует перемещению вдоль прямой, по которой могут катиться колеса, поэтому возникает только одна составляющая 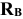, перпендикулярная плоскости качения.

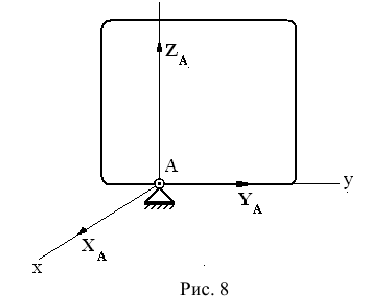
Сферический шарнир (подпятник). В случае сферического шарнира (рис. 8) также нельзя заранее указать направление реакции шарнира При решении задач реакция сферического шарнира заменяется тремя взаимно перпендикулярными составляющими 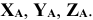(рис. 8).

Жесткая заделка. Такой тип связи будет рассмотрен позже.

Порядок решения задач статики на равновесие твердого тела

Выбирается объект равновесия (некоторое твердое тело):

1. Показываются активные силы, приложенные к объекту равновесия.
2. Применяется аксиома освобождаемости от связей: связи мысленно отбрасываются, а их действие заменяется реакциями связей, приложенными к объекту равновесия.
3. Определяется вид системы сил, действующей на объект равновесия, и составляются соответствующие уравнения (условия) равновесия.
4. Решая уравнения, определяются неизвестные величины.

Эта инструкция для решения задач статики — универсальная, с ее помощью решаются любые задачи статики на равновесие твердого тела. Чаще всего в задачах статики требуется определить реакции связей, т.е. усилия, возникающие в местах закрепления. Условия равновесия, которые применяются в 4-м пункте инструкции, зависят от вида системы сил, действующей на объект равновесия. Можно выделить три основных вида: сходящаяся система сил, произвольная плоская система сил, произвольная пространственная система сил.

Сходящаяся система сил

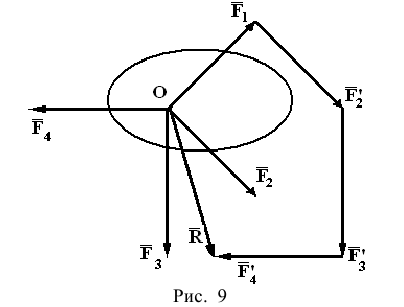
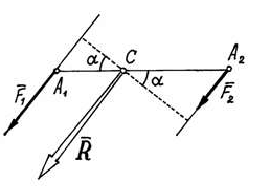
Система сил называется сходящейся, если линии действия сил пересекаются в одной точке. Сходящуюся систему сил можно заменить равнодействующей геометрическим или векторным способом (рис. 9) или аналитически по формулам (1)- (4).

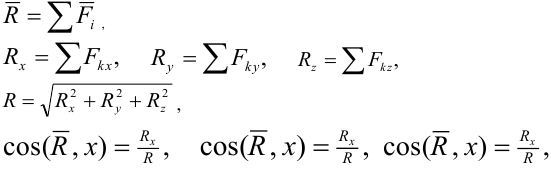
Условия равновесия сходящейся системы сил.

Для равновесия сходящейся системы сил необходимо и достаточно, чтобы выполнялись условия:

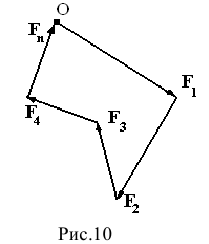
• геометрическое или векторное условие’, силовой многоугольник, построенный на векторах сил как на сторонах должен быть замкнут (рис. 10)

или

• Аналитические уравнения равновесия:

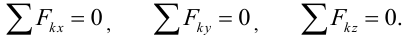
Если все силы сходящейся системы лежат в одной плоскости то следует выбрать систему координат в этой плоскости и использовать только два уравнения.

Произвольная плоская система сил

Если плоская система сил не является сходящейся, то для вывода условий равновесия нужно заменить систему сил на более простую. Это называется приведением системы сил. Для этого нужно ввести дополнительные понятия и термины.

Момент силы относительно точки на плоскости (алгебраический) -это взятое со знаком плюс или минус произведение модуля силы на плечо силы относительно точки. Плечо силы относительно точки — это кратчайшее расстояние от точки до линии действия силы, т е длина перпендикуляра, опущенного из точки на линию действия силы (рис. 11)

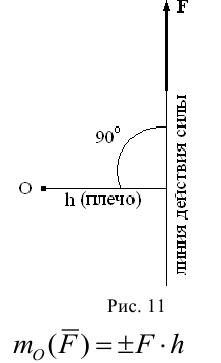
Если сила стремится повернуть плечо против часовой стрелки ( как на рис. 11), то знак момента «+», если по часовой, то « — ».

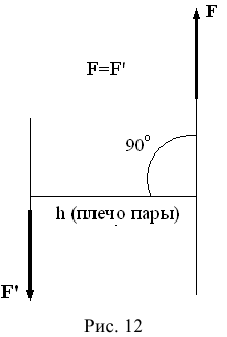
Парой сил называется система двух равных по модулю сил, направленных в противоположные стороны по параллельным линиям действия. Обозначается пара сил 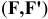. Плечом пары называется расстояние между линиями действия сил, образующих пару. Момент пары (алгебраический на плоскости) это взятое со знаком плюс или минус произведение модуля силы на плечо пары

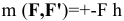
Знак момента выбирается по тому же правилу, что и для момента силы относительно точки. (Рис 12).

Теоремы о свойствах пар в плоскости

1. Момент пары сил равен алгебраической сумме моментов сил образующих пару, вычисленных относительно произвольной точки на плоскости.
2. Две пары сил, лежащие в одной плоскости , эквивалентны тогда и только тогда, когда равны их алгебраические моменты.
3. Система пар сил, лежащих в одной плоскости, эквивалентна одной паре, момент которой равен алгебраической сумме моментов этих пар.
4. Система пар сил, лежащих в одной плоскости, уравновешивается тогда и только тогда, когда алгебраическая сумма моментов этих пар равна нулю.

Из теорем следует, что пара сил создает только вращательное воздействие и для полной характеристики пар, лежащих в одной плоскости достаточно алгебраического момента пары. Поэтому на расчетных схемах задач пары можно показывать в виде символа пары или в виде дуговой стрелки, направленных в сторону вращения, создаваемого парой, и с обозначением или численным значением момента пары (рис. 13).

После введенных понятий момента силы и момента пары, можно рассмотреть еще один типовой вид связи , который называется «жесткая заделка».

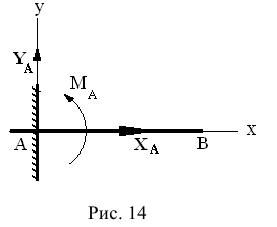
Жесткая заделка.(Рис. 14) Балка не может в месте закрепления ни перемещаться ни вращаться, поэтому реакции такого типа связи имеют составляющие , где 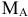— это момент пары сил, противодействующий вращению балки вокруг точки .

По теореме Пуансо произвольную плоскую систему сил можно заменить на одну силу (главный вектор , приложенный в выбранном центре приведения 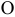) и одну пару сил (главный момент то), лежащую в плоскости действия сил:

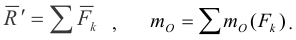
Условия равновесия произвольной плоской системы сил. Для равновесия произвольной плоской системы сил необходимо и достаточно чтобы главный вектор 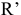и главный момент 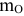относительно произвольно выбранного центра приведения равнялись нулю,

или в аналитической форме

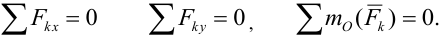
Оси 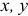системы координат и точку в уравнении моментов можно выбирать произвольно.

Теорема Вариньона для произвольной плоской системы сил.

Если система сил приводится к равнодействующей, то момент равнодействующей относительно произвольной точки равен сумме моментов слагаемых сил относительно той же точки

Произвольная пространственная система сил

Вывод условий равновесия для произвольной пространственной системы сил аналогичен тому, как это проводилось для произвольной плоской системы сил. Только для оценки вращательного воздействия силы и пары сил потребуются векторные моменты силы и пары сил, а также алгебраический момент силы относительно оси.

Векторный момент силы относительно точки в пространстве определяется по формуле:

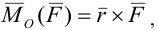
где 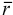— радиус-вектор точки приложения силы 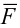(рис. 15).

Введенный таким образом векторный момент силы относительно точки полностью характеризует вращательное воздействие силы, так как определяется плоскость и направление вращения, создаваемого силой, а также численное значение модуля векторного момента равного моменту силы относительно точки в плоскости силы и точки :

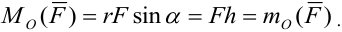
Для оценки вращательного воздействия пары сил также вводится понятие векторного момента пары сил в пространстве. Векторным моментом пары сил называется вектор равный по модулю моменту пары, и направленный перпендикулярно плоскости пары в ту сторону , откуда вращение , создаваемое парой видно против хода часовой стрелки(рис. 16).

Теоремы о свойствах пар в пространстве

Эти теоремы аналогичны теоремам для пар в плоскости:

1. Векторный момент пары сил равен векторной сумме векторных моментов сил образующих пару, вычисленных относительно произвольной точки в пространстве.
2. Две пары сил в пространстве эквивалентны тогда и только тогда, когда равны их векторные моменты.
3. Система пар сил в пространстве эквивалентна одной паре, векторный момент которой равен векторной сумме векторных моментов этих пар.
4. Система пар сил в пространстве уравновешивается тогда и только тогда, когда векторная сумма векторных моментов этих пар равна нулю.

Векторные моменты силы и пары сил — это свободные векторы, их можно переносить в пространстве параллельно себе в любую точку. Момент силы относительно оси в пространстве определяется следующим образом: (рис. 17)

1) проводится плоскость , перпендикулярная оси

2) находится проекция 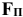силы 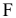на плоскость .

3) момент силы относительно оси находится как алгебраический момент проекции 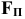относительно точки пересечения оси и плоскости .

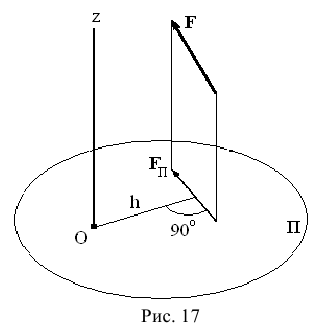
По теореме Пуансо произвольная пространственная система сил приводится к главному вектору и главному моменту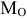

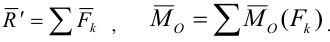
Условия равновесия произвольной пространственной системы сил. Для равновесия произвольной пространственной системы сил необходимо и достаточно чтобы главный вектор 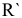и главный момент 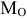относительно произвольно выбранного центра приведения равнялись нулю

или в аналитической форме:

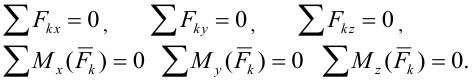
Оси системы координат можно выбирать произвольно.

Равновесие системы тел и расчет ферм

Равновесие системы тел

Статический расчет инженерных сооружений во многих случаях сводится к рассмотрению условий равновесия конструкции из системы тел, соединенных какими — нибудь связями. Связи, соединяющие части данной конструкции, будем называть внутренними, в отличие от внешних связей, скрепляющих конструкцию с телами, в нее не входящими (например, с опорами).

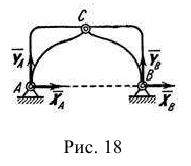
Если после отбрасывания внешних связей (опор) конструкция остается жесткой, то для нее задачи статики решаются как для абсолютно твердого тела.

Однако могут встречаться такие инженерные конструкции, которые после отбрасывания внешних связей не остаются жесткими. Примером такой конструкции является трехшарнирная арка (рис. 22). Если отбросить опоры и 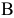, то арка не будет жесткой: ее части могут поворачиваться вокруг шарнира .

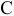На основании принципа отвердевания система сил, действующих на такую конструкцию, должна при равновесии удовлетворять условиям равновесия твердого тела. Но эти условия, как указывалось, будучи необходимыми, не будут являться достаточными, поэтому из них нельзя будет определить всех неизвестных. Для решения задачи необходимо будет дополнительно рассмотреть равновесие какой-нибудь одной или нескольких частей конструкции.

Например, составляя условия равновесия для сил, действующих на трех шарнирную арку (см. рис. 22), мы получим три уравнения с четырьмя неизвестными 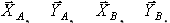Рассмотрев дополнительно условия равновесия левой (или правой) ее половины, мы получим еще три уравнения, содержащие два новых неизвестных 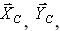на рис. 22 не показанных. Решая полученную систему шести уравнений, найдем все шесть неизвестных.

Другой способ решения подобных задач состоит в том, что конструкцию сразу расчленяют на отдельные тела и составляют условия равновесия каждого из тел, рассматривая его как свободное. При этом реакции внутренних связей будут попарно равны по модулю и противоположны по направлению. Для конструкции из 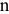тел, на каждое из которых действует произвольная плоская система сил, получится таким путем уравнений, позволяющих найти 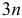неизвестных (при других системах сил число уравнений соответственно изменится). Если для данной конструкции число всех реакций связей будет больше числа уравнений, в которые эти реакции входят, то конструкция будет статически неопределимой.

Расчет ферм. Понятие о ферме. Аналитический расчет плоских ферм

Фермой называется жесткая конструкция из прямолинейных стержней, соединенных на концах шарнирами. Если все стержни фермы лежат в одной плоскости, ферма называется плоской. Места соединения стержней фермы называют узлами. Все внешние нагрузки к ферме прикладываются только в узлах. При расчете фермы трением в узлах и весом стержней (по сравнению с внешними нагрузками) пренебрегают или распределяют веса стержней по узлам. Тогда на каждый из стержней фермы будут действовать две силы, приложенные к его концам, которые при равновесии могут быть направлены только вдоль стержня. Следовательно, можно считать, что стержни фермы работают только на растяжение или на сжатие. Ограничимся рассмотрением жестких плоских ферм, без лишних стержней, образованных из треугольников. В таких фермах число стержней 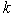и число узлов 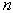связаны соотношением

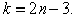
Расчет фермы сводится к определению опорных реакций и усилий в ее стержнях.

Опорные реакции можно найти обычными методами статики, рассматривая ферму в целом как твердое тело. Перейдем к определению усилий в стержнях.

Метод вырезания узлов

Этим методом удобно пользоваться, когда надо найти усилия во всех стержнях фермы. Он сводится к последовательному рассмотрению условий равновесия сил, сходящихся в каждом из узлов фермы. Ход расчетов поясним на конкретном примере.

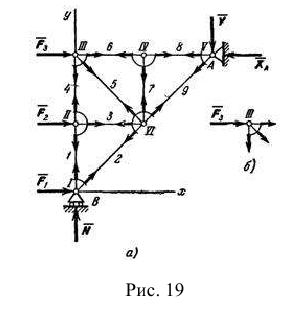
Рассмотрим изображенную на рис. 23,а ферму, образованную из одинаковых равнобедренных прямоугольных треугольников; действующие на ферму силы параллельны оси 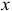и равны:

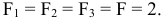
В этой ферме число узлов 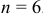, а число стержней 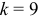. Следовательно, соотношение выполняется и ферма является жесткой, без лишних стержней.

Составляя уравнения равновесия для фермы в целом, найдем, что реакции опор направлены, как показано на рисунке, и численно равны;

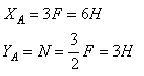
Переходим к определению усилий в стержнях.

Пронумеруем узлы фермы римскими цифрами, а стержни — арабскими. Искомые усилия будем обозначать 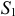(в стержне 1), 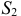(в стержне 2) и т. д. Отрежем мысленно все узлы вместе со сходящимися в них стержнями от остальной фермы. Действие отброшенных частей стержней заменим силами, которые будут направлены вдоль соответствующих стержней и численно равны искомым усилиям 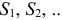. Изображаем сразу все эти силы на рисунке, направляя их от узлов, т. е. считая, все стержни растянутыми (рис. 23, а; изображенную картину надо представлять себе для каждого узла так, как это показано на рис. 23, б для узла III). Если в результате расчета величина усилия в каком-нибудь стержне получится отрицательной, это будет означать, что данный стержень не растянут, а сжат. Буквенных обозначений для сил, действующих вдоль стержней, ни рис. 23 не вводам, поскольку ясно, что силы, действующие вдоль стержня 1, равны численно 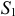, вдоль стержня 2 — равны 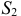и т. д.

Теперь для сил, сходящихся в каждом узле, составляем последовательно уравнения равновесия

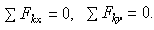
Начинаем с узла 1, где сходятся два стержня, так как из двух уравнений равновесия можно определить только два неизвестных усилия.

Составляя уравнения равновесия для узла 1, получим

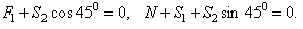
Отсюда находим

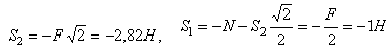
Теперь, зная 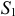, переходим к узлу II. Для него уравнения равновесия дают

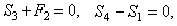
откуда

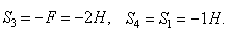
Определив 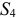, составляем аналогичным путем уравнения равновесия сначала для узла III, а затем для узла IV. Из этих уравнений находим:

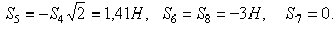
Наконец, для вычисления 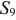составляем уравнение равновесия сил, сходящихся в узле 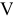, проектируя их на ось 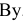. Получим 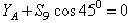, откуда .

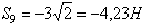Второе уравнение равновесия для узла V и два уравнения для узла VI можно составить как поверочные. Для нахождения усилий в стержнях эти уравнения не понадобились, так как вместо них были использованы три уравнения равновесия всей фермы в целом при определени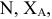и и .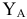

Окончательные результаты расчета можно свести в таблицу:

Как показывают знаки усилий, стержень 5 растянут, остальные стержни сжаты; стержень 7 не нагружен (нулевой, стержень).
Наличие в ферме нулевых стержней, подобных стержню 7, обнаруживается сразу, так как если в узле, не нагруженном внешними силами, сходятся три стержня, из которых два направлены вдоль одной прямой, то усилие в третьем стержне равно нулю. Этот результат получается из уравнения равновесия в проекции на ось, перпендикулярную к упомянутым двум стержням.

Если в ходе расчета встретится узел, для которого число неизвестных больше двух, то можно воспользоваться методом сечений.

1.7.4. Метод сечений (метод Риттера). Этим методом удобно пользоваться для определения усилий в отдельных стержнях фермы, в частности, для проверочных расчетов. Идея метода состоит в том, что ферму разделяют на две части сечением, проходящим через три стержня, в которых (или в одном из которых) требуется определить усилие, и рассматривают равновесие одной из этих частей. Действие отброшенной части заменяют соответствующими силами, направляя их вдоль разрезанных стержней от узлов, т. е. считая стержни растянутыми (как и в методе вырезания узлов). Затем составляют уравнения равновесия, беря центры моментов (или ось проекций) так, чтобы в каждое уравнение вошло только одно неизвестное усилие.

Равновесие с учетом трения

Трение скольжения

Если тело, например, просто лежит на горизонтальной поверхности, то сила трения на него не действует. Трение возникает, если попытаться сдвинуть тело, приложить к нему силу. Пока величина этой силы не превышает определённого значения, тело остаётся в покое и сила трения равна по величине и обратна по направлению приложенной силе. Затем начинается движение.

Сила трения при скольжении твёрдых тел зависит не только от свойств поверхностей и силы давления (это зависимость качественно такая же, как для трения покоя), но и от скорости движения. Часто с увеличением скорости сила трения сначала резко падает, а затем снова начинает возрастать.

Возникновение трения обусловлено, прежде всего, шероховатостью поверхностей, создающей сопротивление перемещению, и наличием сцепления у прижатых друг к другу тел. Изучение всех особенностей явления трения представляет собою довольно сложную физико-механическую проблему, рассмотрение которой выходит за рамки курса теоретической механики.

В инженерных расчетах обычно исходят из ряда установленных опытным путем общих закономерностей, которые с достаточной для практики точностью отражают основные особенности явления трения. Эти закономерности, называемые законами трения скольжения при покое (законами Кулона), можно сформулировать следующим образом:

1. При стремлении сдвинуть одно тело по поверхности другого в плоскости соприкосновения тел возникает сила трения (или сила сцепления), величина которой может принимать любые значения от нуля до значения 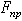, называемого предельной силой трения.

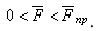
Силой трения скольжения 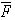(или просто силой трения) называется составляющая силы реакции связи, которая лежит в касательной плоскости к поверхностям соприкасающихся тел.

Сила трения направлена в сторону, противоположную той, куда действующие силы стремятся сдвинуть тело.

В теоретической механике предполагается, что между поверхностями соприкасающихся тел нет смазывающего вещества.

Будем рассматривать два случая: трения при покое или равновесии тела и трение скольжения при движении одного тела по поверхности другого с некоторой относительной скоростью.

При покое сила трения зависит только от активных сил. При выбранном направлении касательной в точке соприкосновения поверхностей тел сила трения вычисляется по формуле:

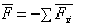
Аналогично при выбранном направлении нормали нормальная реакция выражается через заданные силы:

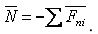
При движении одного тела по поверхности другого сила трения является постоянной величиной.

• Величина предельной силы трения равна произведению статического коэффициента трения на нормальное давление или нормальную реакцию:

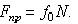
Статический коэффициент трения 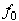— число отвлеченное 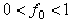; он определяется опытным путем и зависит от материала соприкасающихся тел и состояния поверхностей (характер обработки, температура, влажность, смазка и т. п.). Считается, что коэффициент трения не зависит от скорости движения.

• Предельная сила трения скольжения при прочих равных условиях не зависит от площади соприкосновения трущихся поверхностей. Из этого закона следует, что для того чтобы сдвинуть, например кирпич, надо приложить одну и туже, силу, независимо, от того, какой гранью он положен на поверхность, широкой или узкой.

Объединяя вместе первый и второй законы, получаем, что при равновесии сила трения покоя (сила сцепления)

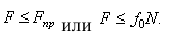
Возможно эта страница вам будет полезна:

Решение задач по теоретической механике

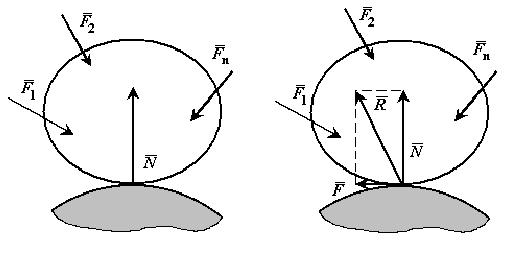
Реакции шероховатых связей. Угол трения

До сих пор при решении задач статики мы пренебрегали трением и считали поверхности связей гладкими, а их реакции направленными по нормалям к этим поверхностям. Реакция реальной (шероховатой) связи будет слагаться из двух составляющих: из нормальной реакции 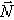и перпендикулярной к ней силы трения 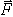. Следовательно, полная реакция 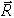будет отклонена от нормали к поверхности на некоторый угол. При изменении силы трения от нуля до 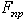сила 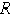будет меняться от 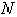до 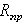, а ее угол с нормалью будет расти от нуля до некоторого предельного значения .

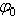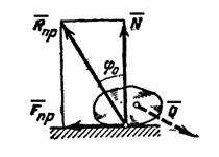
Наибольший угол , который полная реакция шероховатой связи образует с нормалью к поверхности, называется углом трения. Из чертежа видно,что

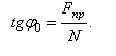
Так как 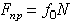, отсюда находим следующую связь между углом трения и коэффициентом трения:

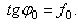
При равновесии полная реакция 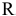, в зависимости от сдвигающих сил, может проходить где угодно внутри угла трения. Когда равновесие становится предельным, реакция будет отклонена от нормали на угол .

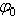Конусом трения называют конус, описанный предельной силой реакции шероховатой связи 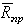вокруг направления нормальной реакции.

Если к телу, лежащему на шероховатой поверхности, приложить силу 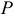, образующую угол 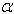с нормалью, то тело сдвинется только тогда, когда сдвигающее усилие 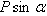будет больше 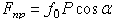(мы считаем N=Pcosa5 пренебрегая весом тела). Но неравенство 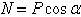в котором 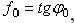выполняется только при 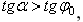те. при .

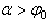Следовательно, никакой силой, образующей с нормалью угол 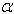, меньший угла трения 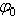, тело вдоль данной поверхности сдвинуть нельзя. Этим объясняются известные явления заклинивания или самоторможения тел.

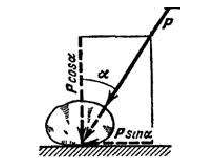
Для равновесия твёрдого тела на шероховатой поверхности необходимо и достаточно, чтобы линия действия равнодействующей активных сил, действующих на твёрдое тело, проходила внутри конуса трения или по его образующей через его вершину.

Тело нельзя вывести из равновесия любой по модулю активной силой, если её линия действия проходит внутри конуса трения.

Равновесие при наличии трения.

Изучение равновесия тел с учетом трения сводится обычно к рассмотрению предельного положения равновесия, когда сила трения достигает своего наибольшего значения 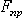. При аналитическом решении задач реакцию шероховатой связи в этом случае изображают двумя составляющими 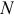и где 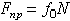. Затем составляют обычные условия равновесия статики, подставляют в них вместо 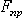величину 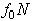и, решая полученные уравнения, определяют искомые величины.

Возможно эта страница вам будет полезна:

Помощь по теоретической механике

Трение качения и верчения

К оглавлению…

Возьмем деревянный цилиндр и положим его на стол так, чтобы он касался стола по образующей. В центры оснований цилиндра вставим концы проволочной вилки и прикрепим к ней снабженный очень чувствительный динамометр. Если тянуть за динамометр, то цилиндр покатится по столу. По показаниям динамометра увидим, что нужна весьма небольшая сила тяги, чтобы сдвинуть с места цилиндр и катить его равномерно дальше, гораздо меньшая, чем при скольжении того же цилиндра, если бы он не вращался и скользил бы по столу. При той же силе давления на стол сила трения качения много меньше силы трения скольжения. Например, при качении стальных колёс по стальным рельсам трение качения примерно в 100 раз меньше, чем трение скольжения. Поэтому в машинах стремятся заменить трение скольжения трением качения, применяя так называемые шариковые или роликовые подшипники.

Происхождение трения качения можно наглядно представить себе так. Когда шар или цилиндр катится по поверхности другого тела, он немного вдавливается в поверхность этого тела, а сам немного сжимается. Таким образом, катящееся тело всё время как бы вкатывается на горку.

Вместе с тем происходит отрыв участков одной поверхности от другой, а силы сцепления, действующие между этими поверхностями, препятствуют этому. Оба эти явления и вызывают силы трения качения. Чем твёрже поверхности, тем меньше вдавливание и тем меньше трение качения.

Трением качения называется сопротивление, возникающее при качении одного тела по поверхности другого.

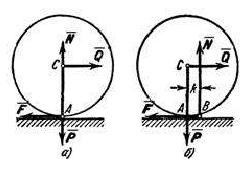
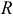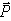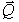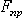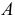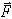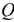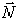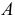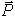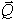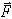Рассмотрим круглый цилиндрический каток радиуса и веса , лежащий на горизонтальной шероховатой плоскости. Приложим к оси катка силу (рис. 34, а), меньшую . Тогда в точке возникает сила трения , численно равная , которая будет препятствовать скольжению цилиндра по плоскости. Если считать нормальную реакцию тоже приложенной в точке , то она уравновесит силу , а силы и образуют пару, вызывающую качение цилиндра. При такой схеме качение должно начаться, как видим, под действием любой, сколь угодно малой силы .

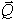Истинная же картина, как показывает опыт, выглядит иначе. Объясняется это тем, что фактически, вследствие деформаций тел, касание их происходит вдоль некоторой площадки 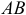(рис. 34, б). При действии силы 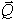интенсивность давлений у края 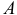убывает, а у края 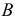возрастает. В результате реакция 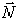оказывается смещенной в сторону действия силы с увеличением 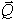это смещение растет до некоторой предельной величины 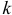. Таким образом, в предельном положении на каток будут действовать пара (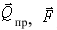) с моментом 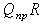и уравновешивающая ее пара (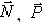) с моментом 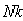. Из равенства моментов находим

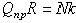
или

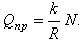
Пока 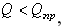каток находится в покое; при 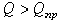начинается качение.

Входящая в формулу линейная величина 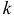называется коэффициентом трения качения. Измеряют величину 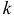обычно в сантиметрах. Значение коэффициента 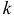зависит от материала тел и определяется опытным путем.

Коэффициент трения качения при качении в первом приближении можно считать не зависящим от угловой скорости качения катка и его скорости скольжения по плоскости.

Для вагонного колеса по рельсу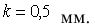

Рассмотрим движение ведомого колес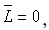а. а .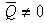

Качение колеса начнется, когда выполнится условие 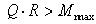или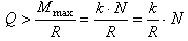

Скольжение колеса начнется, когда выполнится условие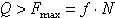

Обычно отношение 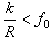и качение начинается раньше скольжения.

Если 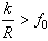, то колесо будет скользить по поверхности, без качения.

Отношение 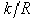для большинства материалов значительно меньше статического коэффициента трения 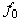. Этим объясняется то, что в технике, когда это возможно, стремятся заменить скольжение качением (колеса, катки, шариковые подшипники и т. п.).

Центр параллельных сил и центр тяжести

Сложение параллельных сил. Центр параллельных сил

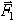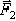Пусть даны две параллельные силы и направленные в одну сторону и приложенные к точкам 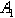и (рис.34).

Конечно, величина их равнодействующей . Вектор её параллелен силам и направлен в ту же сторону. С помощью теоремы Вариньона найдём точку приложения равнодействующей — точку По этой теореме

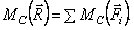
Значит

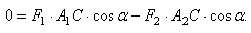
Отсюда 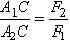. То есть точка приложения равнодействующей делит расстояние между точкам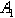и и 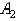на части обратно пропорциональные силам.

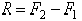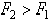Если параллельные силы направлены в противоположные стороны (рис.35), то аналогично можно доказать, что равнодействующая по величине будет равна разности сил: (если ), параллельна им, направлена в сторону большей силы и расположена за большей силой — в точке 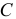. А расстояния от точки до точек приложения сил обратно пропорциональны силам:

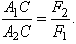
Следует заметить, что если точка приложения равнодействующей расположена на одной прямой с точкам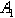и и 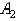точками приложения сил, то, при повороте этих сил в одну сторону на одинаковый угол, равнодействующая также повернётся вокруг точки приложения 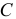в том же направлении, и останется параллельной им.

Такая точка приложения равнодействующей называется центром параллельных сил.

Конечно, если хотя бы одну из сил перенести по своей линии действия в другую точку, то и точка приложения равнодействующей, центр параллельных сил, тоже переместится по линии действия.

Следовательно, положение центра параллельных сил зависит от координат точек приложения сил.

Центром нескольких параллельных сил, найденный последовательным сложением каждых двух сил, будем называть точку 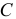, радиус-вектор которой определяется формулой

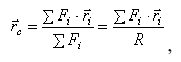
где 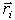— радиусы-векторы точек приложения сил; 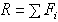— величина равнодействующей параллельных сил, равная алгебраической сумме этих сил (знак силы определяется направлением, которое заранее выбирается и считается положительным).

Используя (1), нетрудно найти координаты центра параллельных сил. Если радиусы-векторы откладывать из начала координат, то проекции радиусов-векторов точек на оси будут равны их координатам. Поэтому, проектируя векторное равенство (1) на оси, получим

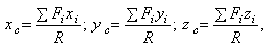
где 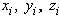— координаты точек приложенных сил.

Возможно эта страница вам будет полезна:

Контрольная работа по теоретической механике

Параллельные силы, распределенные по отрезку прямой

а) общий случай

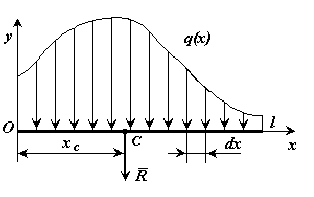
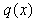— интенсивность распределенной силы [Н/м],

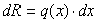— элементарная сила. 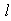— длина отрезка

Распределенная по отрезку прямой сила интенсивности 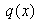эквивалентна сосредоточенной силе

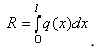
Сосредоточенная сила прикладывается в точке 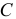(центре параллельных сил) с координатой

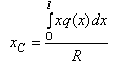
б) постоянная интенсивность

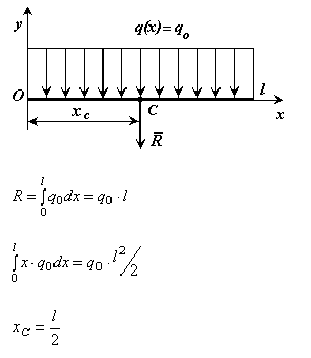
в) интенсивность, меняющаяся по линейному закону

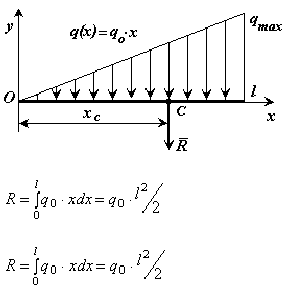
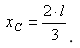
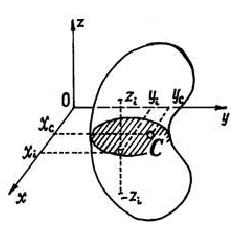
Центр тяжести тел

На все точки тела, находящегося вблизи поверхности Земли, действуют силы — силы тяжести этих точек или их вес 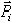. Вообще эти силы будут сходящимися — линии действия их пересекаются в центре Земли. Но, если пренебречь размерами тела в сравнении с размерами Земли, то можно считать их параллельными.

Центр этих параллельных сил, сил тяжести точек, называется центром тяжести тела.

Значит находить центр тяжести тел можно как центр параллельных сил. Например, координаты его

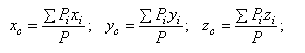
где — вес каждой точки тела, а — вес всего тела.

При определении центра тяжести полезны несколько теорем.

1) Если однородное тело имеет плоскость симметрии, то центр тяжести его находится в этой плоскости.

Если ос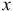и и 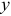расположить в этой плоскости симметрии, то для каждой точки с координатами 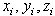можно отыскать точку с координатами 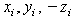и координата 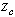по (2), будет равна нулю, т.к. в сумме 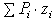все члены имеющие противоположные знаки, попарно уничтожаются. Значит центр тяжести расположен в плоскости симметрии.
2) Если однородное тело имеет ось симметрии, то центр тяжести тела находится на этой оси.

Действительно, в этом случае, если ось 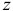провести по оси симметрии, для каждой точки с координатами 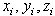можно отыскать точку с координатами 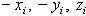и координаты 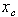и 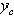, вычисленные по формулам (2), окажутся равными нулю.

Аналогично доказывается и третья теорема.

3) Если однородное тело имеет центр симметрии, то центр тяжести тела находится в этой точке.

И ещё несколько замечаний.

Первое. Если тело можно разделить на части, у которых известны вес и положение центра тяжести, то незачем рассматривать каждую точку, а в формулах (2) 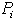— определять как вес соответствующей части и 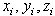— как координаты её центра тяжести.

Второе. Если тело однородное, то вес отдельной части его 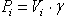, где 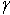— удельный вес материала, из которого сделано тело, а 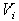— объём этой части тела. И формулы (1) примут более удобный вид. Например,

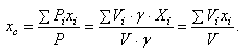
И аналогично,

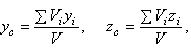
где

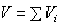
объем всего тела.

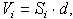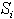Третье замечание. Если тело состоит из однородных пластин одинаковой, малой толщины, то объём каждой пластины где -площадь пластины, 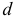— толщина. И координаты центра тяжести будут определяться только с помощью площадей:

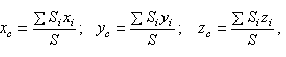
где 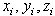— координаты центра тяжести отдельных пластин; 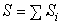— общая площадь тела.

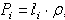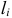Четвёртое замечание. Если тело состоит из стержней, прямых или криволинейных, однородных и постоянного сечения, то вес их где , — длина, 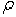— вес единицы длины (погонного метра), а координаты центра тяжести будут определяться с помощью длин отдельных участков:

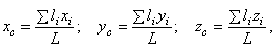
где 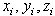— координаты центра тяжести 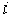-го участка;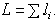

Отметим, что согласно определению центр тяжести — это точка геометрическая; она может лежать и вне пределов данного тела (например, для кольца).

Координаты центров тяжести неоднородных тел.

Координаты центра тяжести неоднородного твердого тела в выбранной системе отсчета определяются следующим образом:

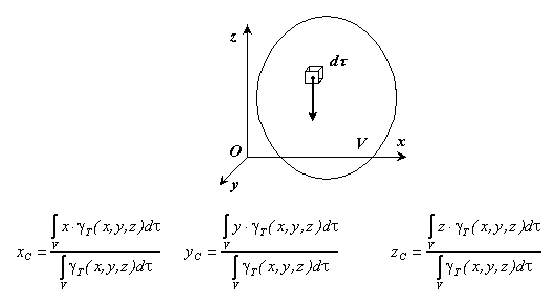
где 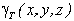— вес единицы объем тела (удельный вес); 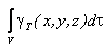— вес всего тела.

Если твердое тело представляет собой неоднородную поверхность, то координаты центра тяжести в выбранной системе отсчета определяются следующим образом:

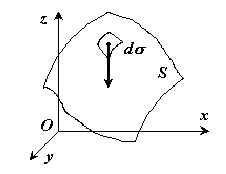
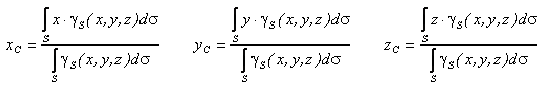
где 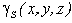— вес единицы площади тела, 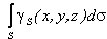— вес всего тела.

Если твердое тело представляет собой неоднородную линию, то координаты центра тяжести в выбранной системе отсчета определяются следующим образом:

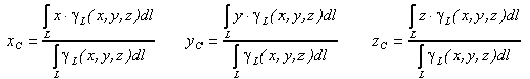
где 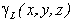— вес единицы длины тела, 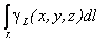— вес всего тела.

Координаты центров тяжести однородных тел.

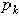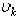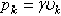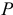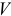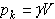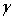Для однородного тела вес любой его части пропорционален объему этой части:, а вес всего тела пропорционален объему этого тела , где — вес единицы объема.

Подставив эти значения и в предыдущие формулы, мы заметим, что в числителе 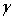как общий множитель выносится за скобку и сокращается с 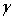в знаменателе. В результате получим:

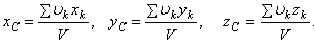
Как видно, центр тяжести однородного тела зависит только от его геометрической формы, а от величины 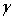не зависит. По этой причине точку 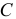, координаты которой определяются формулами, называют центром тяжести объема .

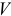Путем аналогичных рассуждений легко найти, что если тело представляет собой однородную плоскую и тонкую пластину, то для нее

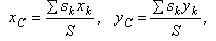
где 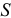— площадь всей пластины, a 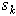— площади ее частей.

Точку, координаты которой определяются формулами называют центром тяжести площади .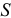

Точно так же получаются формулы для координат центра тяжести линии:

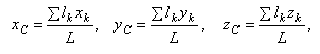
где 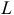— длина всей линии, 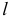— длины ее частей.

Таким образом, центр тяжести однородного тела определяется, как центр тяжести соответствующего объема, площади или линии.

Способы определения координат центра тяжести

Исходя из полученных выше общих формул, можно указать конкретные способы определения координат центров тяжести тел.

Симметрия. Если однородное тело имеет плоскость, ось или центр симметрии, то его центр тяжести лежит соответственно в плоскости симметрии, оси симметрии или в центре симметрии.

Разбиение. Тело разбивается на конечное число частей, для каждой из которых положение центра тяжести и площадь известны.

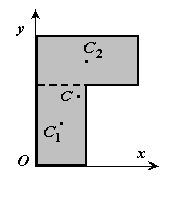
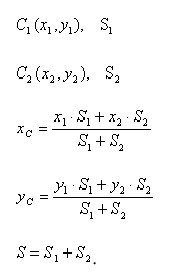
Дополнение. Частный случай способа разбиения. Он применяется к телам, имеющим вырезы, если центры тяжести тела без выреза и вырезанной части известны.

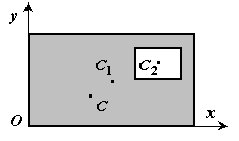
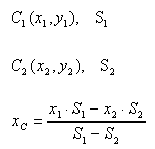
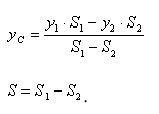
Центры тяжести некоторых однородных тел.

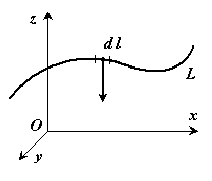
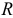1) Центр тяжести дуги окружности. Рассмотрим дугу радиуса с центральным углом в силу симметрии центр тяжести этой дуги лежит на оси .

Найдем координату 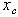по формуле 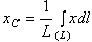. Для этого выделим на дуге элемент длиною 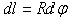положение которого определяется углом 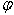. Координата 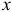элемента будет 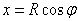. Подставляя эти значения 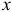и 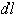и имея в виду, что интеграл должен быть распространен на всю длину дуги, получим:

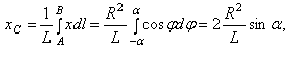
где 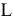— длина дуги 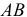, равная 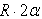. Отсюда окончательно находим, что центр тяжести дуги окружности лежит на ее оси симметрии на расстоянии от центра 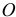, равном

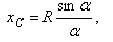
где угол 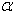измеряется в радианах.

2) Центр тяжести площади треугольника. Разобьем площадь треугольника 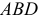прямыми, параллельными 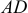, на узкие полоски; центры тяжести этих полосок будут лежать на медиане 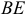треугольника.

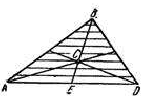
Следовательно, и центр тяжести всего треугольника лежит на этой медиане. Аналогичный результат получается для двух других медиан. Отсюда заключаем, что центр тяжести площади треугольника лежит в точке пересечения его медиан.

При этом, как известно,

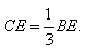
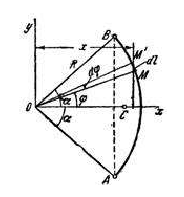
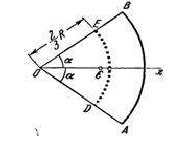
3) Центр тяжести площади кругового сектора. Рассмотрим круговой сектор 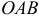радиуса 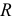с центральным углом . Разобьем мысленно площадь сектора 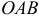радиусами, проведенными из центра , на 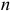секторов. В пределе, при неограниченном увеличении числа 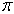, эти секторы можно рассматривать как плоские треугольники, центры тяжести которых лежат на дуге 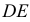радиуса 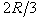. Следовательно, центр тяжести сектора будет совпадать с центром тяжести дуги . Окончательно получим, что центр тяжести площади кругового сектора лежит на его центральной оси симметрии на расстоянии от начального центра , равном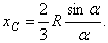

Возможно эта страница вам будет полезна:

Курсовая работа по теоретической механике

Кинематика

Кинематика точки

Кинематика это раздел теоретической механики, в котором изучаются движения точек и тел без учета сил, вызывающих это движение.

В кинематике можно выделить две задачи:

1 -я — описать (задать) движение объекта (точки или тела)

2-я — по описанному (заданному) движению объекта определить характеристики его движения.

Три способа описания движения точки.

Векторный способ описания движения точки. Положение точки определяется ее радиус-вектором, проведенным из какого-либо центра, который, изменяясь во времени, определяет движение точки, 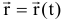это уравнение движения точки в векторной форме. Траектория движения точки — это непрерывная линия по которой движется точка. Координатный способ описания движения точки. Положение точки в пространстве определяется тремя координатами, изменения которых определяют закон движения точки:

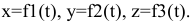
Если точка движется в плоскости, то уравнений движения два, если по прямой то одно.. Уравнения движения описывают уравнение траектории в параметрической форме. Исключив из уравнений параметр 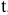, получаем уравнение траектории в обычном виде: 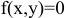(для плоскости). Если в пространстве, то исключив параметр 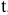, получим два уравнения , которые совместно определяют траекторию движения точки в пространстве. Естественный способ описания движения точки. Указывается траектория движения точки и закон ее движения по этой траектории, начало и направление отсчета дуговой координаты, а также 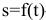— закон движения точки. При прямолинейном движении: 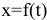, и естественный и координатный способы тождественны Связь между координатным и векторным способами:

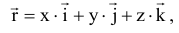
где 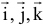— орты — единичные вектора, направленные соответственно по осям .

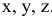Переход от координатного способа к естественному можно осуществить по формуле:.

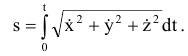
Скорость точки. Скорость точки это вектор, характеризующий изменение положения точки в единицу времени. Вектор скорости определяется по формуле:

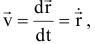
точка обозначает производную по времени, или

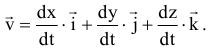
При координатном способе описания движения точки вначале определяются проекции скорости на оси координат :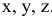

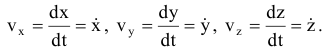
Модуль скорости:

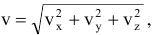
направляющие косинусы:

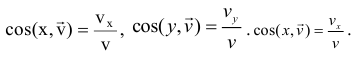
При естественном способе описания движения точки модуль скорости

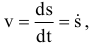
вектор скорости

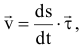
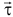— орт касательной, т.е. скорость всегда направлена по касательной к траектории. Если 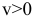, то движение происходит в сторону положительного отсчета дуговой координаты и наоборот.

Ускорение точки.

При векторном способе

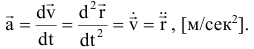
Проекция ускорения:

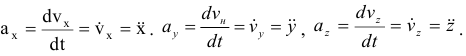
Модуль ускорения:

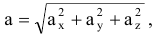
направляющие косинусы:

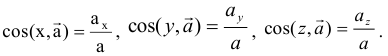
При естественном способе описания движения точки полное ускорение раскладывают на нормальное и касательное (тангенциальное) ускорения:

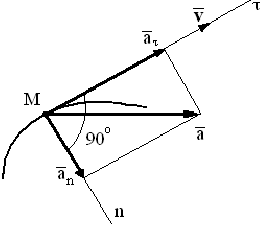
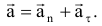
Модуль нормального ускорения:

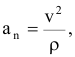
где 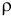— радиус кривизны траектории, нормальное ускорение направлено по нормали к траектории ( 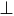к касательной) всегда к центру кривизны, т.е. в сторону вогнутости.

Нормальное ускорение характеризует изменение скорости по направлению.

Модуль касательного ускорения

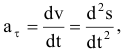
направлено по касательной к траектории, либо в сторону скорости, либо в обратную. Касательное ускорение характеризует изменение скорости по величине. При ускоренном движении направление касательного ускорения и скорости совпадают, при замедленном — противоположно. 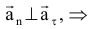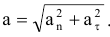Вектор ускорения лежит в соприкасающейся плоскости 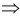его проекция на бинормаль равна 0 (главная нормаль лежит в соприкасающейся плоскости, т.е. в плоскости плоской кривой, бинормаль перпендикулярна к главной нормали и касательной). Частные случаи движения точки:

1 (Прямолинейное: радиус кривизны 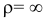(бесконечно большой)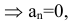

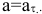
2)Равномерное криволинейное движение: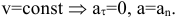. Ускорение возникает из-за изменения направления скорости. Закон движения: 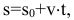, при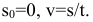

3)Равномерное прямолинейное движение: 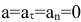. Единственное движение, где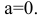

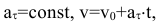
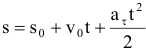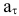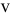4)Равнопеременное криволинейное движение: . При равноускоренном, движении знаки у и одинаковы, при равнозамедленном — разные.

Кинематика твердого тела

К оглавлению…

Простейшие движения твердого тела: поступательное и вращательное

Поступательное движение тела — это такое движение твердого тела, при котором любая прямая, проведенная в этом теле, перемещается, оставаясь параллельное самой себе. При поступательное движении, все точки тела описывают одинаковые траектории и имеют в каждый момент времени одинаковые по модулю и направлению скорости и ускорения. Вращательное движение тела — это такое движение твердого тела, при котором все точки, принадлежащие некоторой прямой, неизменно связанной с телом, остаются неподвижными. Эта прямая называется осью вращения тела.

При этом движении все точки тела движутся в плоскостях, перпендикулярных оси вращения, и описывают окружности, центры которых лежат на оси вращения. Уравнение (закон) вращательного движения: 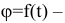угол поворота тела в радианах.

Угловая скорость:

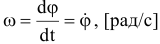
определяет изменение угла поворота в единицу времени.

Вектор угловой скорости тела, совершающего вращение вокруг неподвижной оси, направлен вдоль оси вращения так, что если смотреть ему навстречу вращение будет против часовой стрелке, 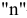— число оборотов в

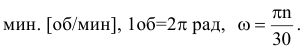
Угловое ускорение тела:

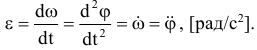
Вектор углового ускорения также направлен вдоль оси вращения. При ускоренном движении совпадает по направлению с угловой скоростью и противоположно при замедленном вращении.

Частные случаи вращения тела: 1) Равномерное вращение:

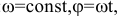
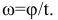
2) Равнопеременное вращение:

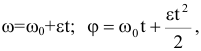
здесь начальный угол

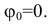
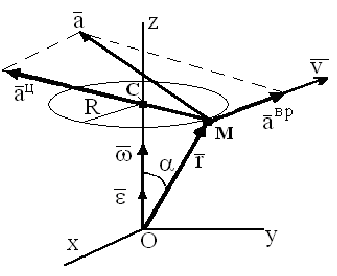
Скорости и ускорения точек вращающегося тела, 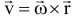— скорость любой точки твердого тела, вращающегося вокруг неподвижной оси, равна векторному произведению вектора угловой скорости тела на радиус-вектор этой точки. Модуль векторного произведения:

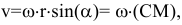
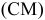-расстояние от точки до оси вращения. Направлен вектор скорости по касательной к окружности, по которой перемещается точка , в сторону вращения. Формула Эйлера:

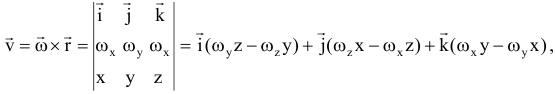
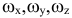— проекции вектора угловой скорости. Проекция вращательной (окружной) скорости:

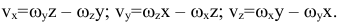
Если ось вращения совпадает с осью 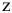, то 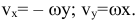. Ускорение:

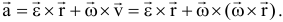
Вращательное (касательное, тангенциальное) ускорение

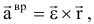
модуль вращательного, ускорения

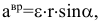
направлено по касательной к траектории точки, т.е. параллельно скорости. Центростремительное (осестремительное, нормальное) ускорение

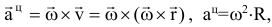
направлено по радиусу к оси (центру) вращения. Модуль полного ускорения.:

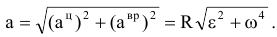
Угол, между векторами полного и центростремительного ускорений:

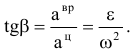
Сложное движение точки. — такое движение, при котором точка одновременно участвует в нескольких движениях (например, пассажир, перемещающийся по движущемуся вагону). В этом случае вводится подвижная система координат , которая совершает заданное движение относительно неподвижной (основной) системы координат .

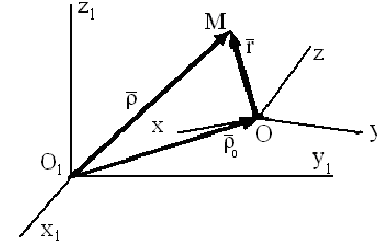
Абсолютным движением точки называется движение по отношению к неподвижной системе координат. Относительное движение — движение по отношению к подвижной системе координат, (движение по вагону). Переносное движение — движение подвижной системе, координат относительно неподвижной (движение вагона). Теорема о сложении скоростей:

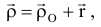
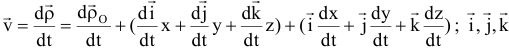
орты (единичные вектора) подвижной системы координат, орт вращается вокруг мгновенной оси, поэтому скорость его конца

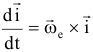
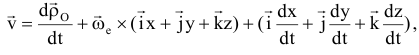
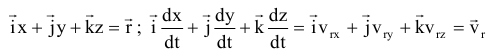
относительная скорость.

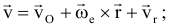
переносная скорость:

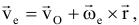
поэтому абсолютная скорость точки = геометрической сумме ее переносной 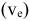и относительной 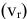скоростей 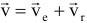модуль:

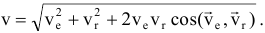
Теорема о сложении ускорений (теорема Кориолиса):

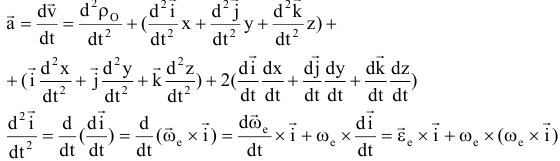
Слагаемые выражения, определяющего ускорения :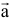

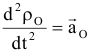
ускорение полюса ;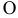

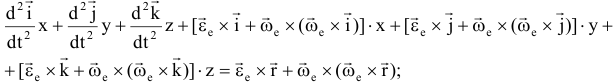
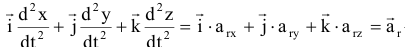
относительное ускорение точки;

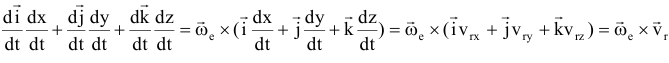
получаем:

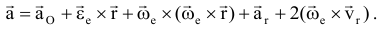
Первые три слагаемых представляют собой ускорение точки в переносном движении: 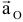— ускорение полюса 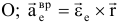— вращательное уск., 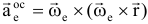— осестремительное ускорение., т.е.

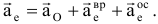
Теорема о сложении ускорений (теорема Кориолиса):

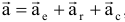
где

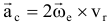
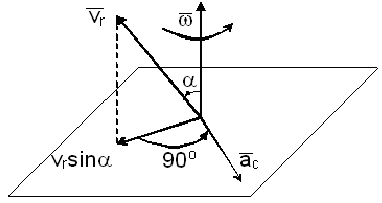
ускорение Кориолиса (кориолисово ускорение) — в случае непоступательного переносного движения абсолютное ускорение = геометрической сумме переносного, относительного и кориолисова ускорений. Кориолисово ускорение характеризует: 1) изменение модуля и направления переносной скорости точки из-за ее относительного движения; 2) изменение направления относительной скорости точки из-за вращательного переносного движения. Модуль ускорения Кориолиса:

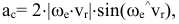
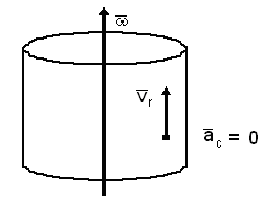
направление вектора 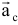с определяется по правилу векторного произведения, или по правилу Жуковского: проекцию относительной скорости на плоскость, перпендикулярную переносной угловой скорости, надо повернуть на 90° в направлении вращения. Кориолисово ускорение = 0 в трех случаях: 1) 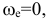, т.е. в случае поступательного переносного движения или в момент обращения угловой, скорости в 0; 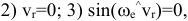т.е. 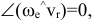когда относительная скорость 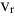параллельна оси переносного вращения.

В случае движения в одной плоскости — угол между 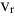и вектором

Плоскопараллельное движение твердого тела

К оглавлению…

Плоскопараллельным называется такое движение тела, при котором все его точки перемещаются параллельно некоторой неподвижной плоскости. Уравнения плоского движения:

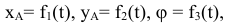
точка 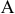называется, полюсом. Плоскопараллельное движение твердого тела раскладывается на поступательное движение, при котором все точки тела движутся так же, как полюс 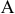и вращательное движение вокруг этого полюса. Поступательное перемещение зависит от выбора полюса, а величина и направление угла поворота не зависят. Скорости точек тела при плоском движении:

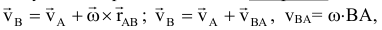
т.е. скорость какой-либо точки 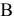плоской фигуры равна геометрической сумме скорости полюса 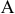и скорости точки 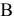при вращении плоской фигуры вокруг полюса .

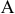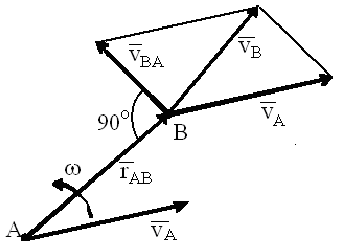
Теорема о проекциях скоростей точек плоской фигуры. При плоском движении проекции скоростей двух точек тела на прямую, соединяющую эти точки равны между собой:

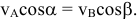
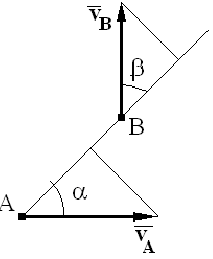
Мгновенный центр скоростей (сокращенно м.ц.с.) — точка плоской фигуры, скорость которой в данный момент времени равна нулю. Если тело движется непоступательно, т.е. 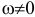, то мгновенный центр скоростей всегда существует. При поступательном движении м.ц.с. находится в 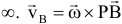— скорость любой точки плоской фигуры имеет модуль, равный произведению угловой скорости фигуры на длину отрезка, соединяющего точку с м.ц.с., и направлена 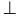этому отрезку в сторону вращения фигуры.

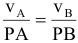скорости точек тела пропорциональны их расстояниям до м.ц.с.

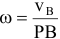угловая скорость тела равна отношению скорости какой-нибудь точки к ее расстоянию до м.ц.с.

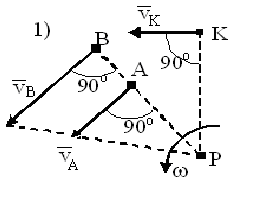
Определение положения м.ц.с.

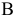1) м.ц.с. — точка пересечения перпендикуляров, восстановленных к скоростям точек (напр. в точке и точке ); 2) если скорости точек и параллельны между собой и перпендикулярны 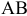, то для определения м.ц.с. должны быть известны модули и направления скоростей (см. 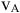и 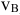); 3) если они при этом равны между собой, то м.ц.с. находится в 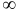, а угловая скорость 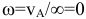; 4) если известно, что скорости двух точек 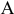и 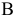равны, параллельны и не перпендикулярны 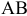, то м.ц.с. в , и угловая скорость , если это имеет место только к некоторый момент времени, то имеем мгновенное поступательное движение; 5) если плоская фигура катится без скольжения по неподвижной поверхности, то м.ц.с. плоской фигуры будет в точке соприкасания.

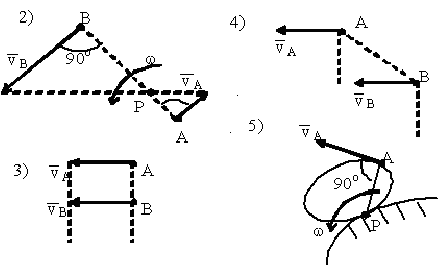
Теорема Шаля: плоскую фигуру можно переместить из одного положения в любое другое положение на плоскости одним поворотом этой фигуры вокруг некоторого неподвижного центра. Этот центр на неподвижной плоскости, совпадает с м.ц.с. и называется мгновенным центром вращений (ось вращений). При движении плоской фигуры м.ц.с. непрерывно изменяет свое положение. Геометрическое место м.ц.с., отмеченных на неподвижной плоскости, называется неподвижной центроидой. Геометрическое место м.ц.с., отмеченных на плоскости фигуры, называется, подвижной центроидой (колесо катится по прямой: неподвижная центроида — прямая, подвижная -окружность). При движении плоской фигуры подвижная центроида катится без скольжения по неподвижной центроиде (теорема Пуансо).

Ускорение точек:

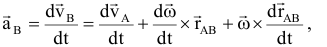
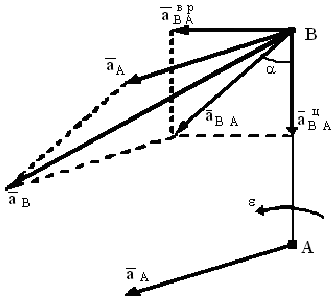
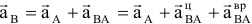— ускорение любой точки () фигуры геометрически складывается из ускорения полюса (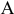) и центростремительного и вращательного ускорений во вращательном движении тела относительно полюса.

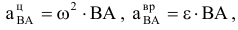
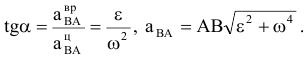
Мгновенный центр ускорений (сокращенно м.ц.у.) — точка (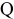) плоской фигуры, ускорение которой в данный момент времени равно нулю. Для его построения из точки 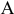откладываем под углом 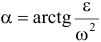к ускорению 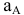отрезок 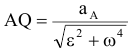при этом угол откладывается от ускорения в сторону, направления углового ускорения 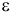. Модули ускорений точек плоской фигуры пропорциональны расстояниям от этих точек до мгновенного центра ускорений, а векторы ускорений составляют с отрезками, соединяющими эти точки и м.ц.у. один и тот же угол

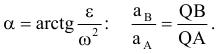
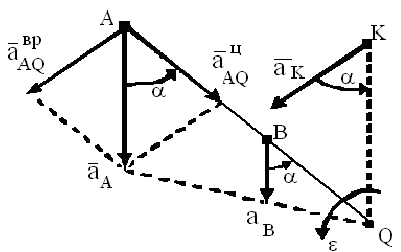
Мгновенный центр скоростей и мгновенный центр ускорений являются различными точками плоской фигуры.