Оглавление:

| Здравствуйте! Я Людмила Анатольевна Фирмаль, занимаюсь помощью студентам более 17 лет. У меня своя команда грамотных, сильных преподавателей. Мы справимся с любой поставленной перед нами работой технического и гуманитарного плана. И неважно – она по объёму на две формулы или огромная, сложно структурированная, на 125 страниц! Нам по силам всё, поэтому не стесняйтесь, присылайте. |
| Если что-то непонятно — вы всегда можете написать мне в WhatsApp и я вам помогу! |
Как заказать выполнение заданий по теоретическим основам электротехники (ТОЭ)
Вы можете написать сообщение в WhatsApp. После этого я оценю ваш заказ и укажу стоимость и срок выполнения вашей работы. Если условия Вас устроят, Вы оплатите, и преподаватель, который ответственен за вашу работу, начнёт выполнение и в согласованный срок или, возможно, раньше срока Вы получите файл готовой работы в личные сообщения.
Сколько может стоить заказ
Стоимость заказа зависит от задания и требований Вашего учебного заведения. На цену влияют: сложность, количество заданий и срок выполнения. Поэтому для оценки стоимости заказа максимально качественно сфотографируйте или пришлите файл задания, при необходимости, загружайте поясняющие фотографии лекций, файлы методичек, указывайте свой вариант.
Какой срок выполнения заказа
Минимальный срок выполнения заказа составляет 2-4 дня, но помните, срочные задания оцениваются дороже.
Как оплатить заказ
Сначала пришлите задание, я оценю, после вышлю вам форму оплаты, в которой можно оплатить с баланса мобильного телефона, картой Visa и MasterCard, apple pay, google pay.
Гарантии и исправление ошибок
В течение 1 года с момента получения Вами готового решения заказа действует гарантия. В течении 1 года я и моя команда исправим любые ошибки в заказе.
Чуть ниже я подготовила краткую теорию по всему курсу теоретических основ электротехники, чтобы вы освежили память, когда получите от меня готовую работу, подготовьтесь к сдаче по этой теории.
Введение
Дисциплина «Теоретические основы электротехники» занимает основное место среди общетехнических дисциплин студентов и слушателей электротехнических специальностей и определяет теоретический уровень профессиональной подготовки специалиста.
Предмет изучения дисциплины составляют электромагнитные явления и их прикладное применение для производства, передачи и распределения электрической энергии между источниками энергии и потребителями, для решения проблем электроэнергии, электромеханики, электроники, автоматики, информационно-измерительной и вычислительной техники.
«Теоретические основы электротехники» как базовая дисциплина должна обеспечивать комплексную подготовку будущего специалиста — профессиональную подготовку, развитие творческих способностей, умение формулировать и решать на высоком уровне задачи специальных дисциплин, умение творчески применять и самостоятельно повышать свои знания.
Основные задачи изучения курса «Теоретические основы электротехники»:
- изучение одной из форм материн электромагнитного поля и его проявлений в различных устройствах техники;
- усвоение современных методов моделирования электромагнитных процессов, методов анализ, синтеза и расчета электрических и магнитных цепей, знание которых необходимо для понимания и успешного решения инженерных проблем будущей специальности.
Свойства линейных электрических цепей
Основные понятия и определении
Электромагнитный объект с протекающими в нем и окружающем его пространстве физическими процессами принято заменять расчетным эквивалентом — электрической цепью. Электрическая цепь — совокупность устройств предназначенная для генерирования, преобразования, передачи и использования электрической энергии. Отдельные устройства входящие в электрическую цепь называются элементами электрической цепи.
В общем случае простейшая электрическая цепь содержит три основных элемента:
- источник электрической энергии,
- приемник электрической энергии,
- коммуникации или соединительные провода.
Кроме перечисленных элементов электрическая цепь может содержать: выключатели и рубильники, электроизмерительные приборы, преобразовательные устройства (трансформаторы, выпрямители, инверторы и др.).
Электромагнитные процессы в электрических цепях можно описать с помощью таких понятий как: ЭДС, напряжение, ток, сопротивление, проводимость, индуктивность, емкость, частота.
Электродвижущая сила (ЭДС) источника питания (ИП) — способность ИП создавать и поддерживать разность потенциалов на своих зажимах, а также возбуждать и поддерживать эл. ток в замкнутой цепи. ЭДС численно равна той энергии которую приобретает положительный заряд равный 1 Кулон перемещаясь по источнику под действием сторонних сил.
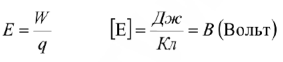
Под напряжением на участке цепи понимают разность потенциалов между крайними точками этого участка.
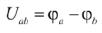
Электрический ток — направленное упорядоченное движение частиц вещества имеющих электрические заряды. Величина тока определяется количеством электричества (электрических зарядов в 1 Кл) проходящего через поперечное сечение проводника в единицу времени. Электрический ток не изменяющийся по величине и направлению называется постоянным, в противном случае переменным.
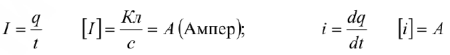
Способность электроприемников (ЭП) поглощать электрическую энергию и преобразовывать ее в другие виды энергии, а также создавать свои электрические и магнитные поля принято характеризовать понятиями: сопротивление 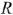 , проводимость
, проводимость 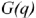 , индуктивность
, индуктивность 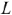 , емкость
, емкость 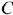 .
.
Сопротивление характеризует способность элемента поглощать электрическую энергию и преобразовывать ее в другие виды (тепловую, световую и т.д.)

где, 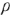 — удельное сопротивление материала, Ом ;
— удельное сопротивление материала, Ом ; 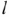 — длина, м;
— длина, м; 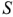 поперечное сечение,
поперечное сечение, 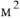 .
.
Проводимости — величина обратная сопротивлению
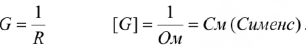
Индуктивность характеризует способность элемента создавать свое магнитное поле 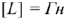 (Генри).
(Генри).
Емкость характеризует способность элемента цепи создавать свое электрическое поле 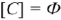 (Фарад).
(Фарад).
Основной характеристикой каждого параметра является вольт-амперная, вебер-амнерная и кулон-волыная зависимости.
В общем случае любое электротехническое устройство обладает всеми перечисленными параметрами 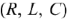 . Однако часто работу одного и того же устройства приближенно можно характеризовать лишь одним параметром.
. Однако часто работу одного и того же устройства приближенно можно характеризовать лишь одним параметром.
Например, лампа накаливания представляет собой сопротивление, некоторые обмотки электрических машин обладают лишь индуктивностью и т.д. Элементы электрической цепи, обладающие только одним параметром, называются идеальными.
В том случае, когда характеристики элементов 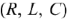 являются линейными или не значительно отличаются от них, т.е. параметры элементов не зависят от напряжений и токов в цепи, эти элементы называются линейными. Электрическая цепь состоящая из линейных элементов называется линейной. В том случае, когда электрическая цепь содержит хотя бы один нелинейный элемент ее называю! нелинейной.
являются линейными или не значительно отличаются от них, т.е. параметры элементов не зависят от напряжений и токов в цепи, эти элементы называются линейными. Электрическая цепь состоящая из линейных элементов называется линейной. В том случае, когда электрическая цепь содержит хотя бы один нелинейный элемент ее называю! нелинейной.
Схемы электрических цепей
Эл. цепь на чертежах изображается в виде схемы пол которой слслует понимать графическое изображение цепи, содержащее стандартные обозначения ее элементов и связь между ними.
Для упрощения анализа реальную эл. цепь представляют математической моделью — набором идеальных элементов. Графическое изображение эл. цепи с помощью стандартных обозначений идеальных элементов отражающих при определенных условиях свойства реальной цепи принято называть схемой замещения.
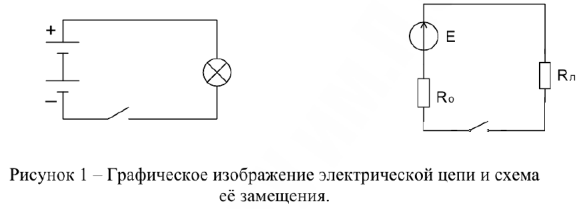
Эл. цепь и соответствующая ей схема замещения состоит из ветвей и узлов. Ветвь — последовательное соединение нескольких элементов, по которым протекает один и тот же ток. Узел — место соединения трех и более ветвей. На каждом из параллельно соединенных элементов присутствует одно и то же падение напряжения. Цепь, содержащая последовательное и параллельное соединение элементов называется разветвленной, а само соединение элементов — смешанным.
Контур эл. цепи — замкнутый путь проходящий по нескольким ветвям. Разветвленная эл. цепь является многоконтурной. Контуры эл. цепи отличающиеся друг от друга хотя бы одним элементом или ветвыо, называются независимыми. Участок цепи, имеющий два зажима или полюса, называется двухполюсным.
Условные положительные направления
Одно из двух возможных направлений напряжения или тока называется условно положительным направлением (УПН). Для определенности описания процессов происходящих в эл. цепях в электротехнике принято:
- за УПН ЭДС считать направление действия сторонних сил на положительный заряд внутри источника питания (ИП);
- за УПН тока — направление движения положительного заряда во внешней цепи, т.е. направление тока от более высокого потенциала к более низкому;
- за УПН напряжения — направление убывания потенциала. Из приведенного следует:
- УПН тока и напряжения на пассивном элементе совпадают;
- УПН напряжения на источнике ЭДС противоположно УПН ЭДС.
Схемы замещении и характеристики источников питания
Различают следующие виды источников питания: источник ЭДС и источник тока.
Схема замещения и ВАХ источника ЭДС имеют следующий вид:
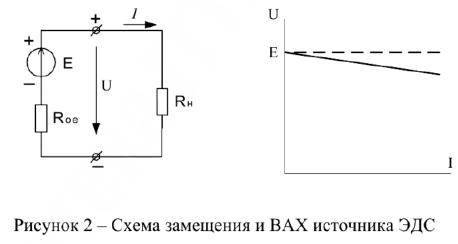
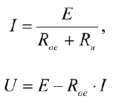
Пунктирной линией обозначена ВАХ идеального источника ЭДС 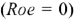 , а сплошной — реального
, а сплошной — реального 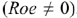 . Внутреннее сопротивление реального источника ЭДС очень маленькое и. как правило, на много меньше сопротивления нагрузки.
. Внутреннее сопротивление реального источника ЭДС очень маленькое и. как правило, на много меньше сопротивления нагрузки.
Схема замещения и ВАХ источника тока имеют следующий вид:
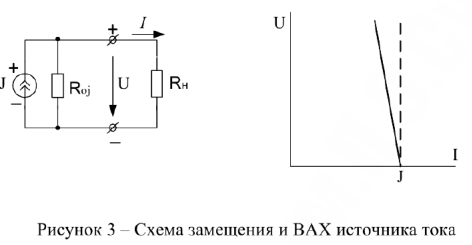
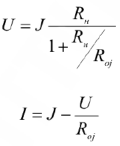
Пунктирной линией обозначена ВАХ идеального источника тока 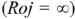 , а сплошной — реального
, а сплошной — реального 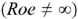 . Внутреннее сопротивление реального источника тока очень большое и, как правило, на много больше сопротивления нагрузки.
. Внутреннее сопротивление реального источника тока очень большое и, как правило, на много больше сопротивления нагрузки.
Таким образом, можно дать определение рассмотренных источников питания. Источник ЭДС — это устройство способное генерировать на своих зажимах напряжение практически (реальный источник ЭДС), либо абсолютно (идеальный источник ЭДС) независимое от нагрузки. Источник тока — это устройство способное вырабатывать ток практически (реальный источник тока), либо абсолютно (идеальный источник тока) независимый от нагрузки.
Режимы работы электрических цепей
Различают следующие режимы работы эл. цепей: режим холостого хода (Х.Х.), режим короткого замыкания (К.З.) и нагрузочный режим.
Для источника ЭДС в режиме Х.Х. ток равен нулю, а напряжение равно ЭДС. В режиме К.З. ток равен току короткого замыкания, а напряжение равно нулю. Для источника ЭДС режим К.З. является аварийным.
Для источника тока в режиме Х.Х. ток равен нулю, а напряжение стремится к бесконечности. Для источника тока режим Х.Х. является аварийным. В режиме К.З. ток равен току источника, а напряжение равно нулю.
Среди нагрузочных режимов выделяют номинальный режим и режим согласованной нагрузки. Номинальный режим работы ИП или элсктроприсмника (ЭП) характеризуется тем, что напряжение, ток и мощность его соответствуют тем значениям, на которые он рассчитан заводом изготовителем, при этом ИП или ЭП работает без нагрева и без других недопустимых последствий длительное время. Согласованным называется режим работы цепи, когда сопротивление нагрузки равно внутреннему сопротивлению ИП. В согласованном режиме мощность, потребляемая приемником -максимальна. В силовых электроустановках такой режим не экономичен, т.к. в ней выделяется лишь 50% потребляемой мощности, остальные 50% выделяются в ИП и соединительных коммуникациях в виде потерь.
Основные законы электрических цепей
Закон Ома
Под законом Ома можно понимать все соотношения, связывающие между собой напряжение и ток. По закону Ома напряжение на резистивном элементе пропорционально току в нем. Коэффициент пропорциональности назван сопротивлением: 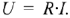 . Закон Ома также можно записать относительно тока. Рассмотрим правила записи закона Ома для участка цепи содержащего активное сопротивление и источник ЭДС.
. Закон Ома также можно записать относительно тока. Рассмотрим правила записи закона Ома для участка цепи содержащего активное сопротивление и источник ЭДС.
Если ток в нагрузке совпадает по направлению с ЭДС, последняя работает как источник энергии (рис. 4). В противном случае когда направление тока в нагрузке встречно с направлением ЭДС источник работает в качестве приемника энергии (рис. 5).
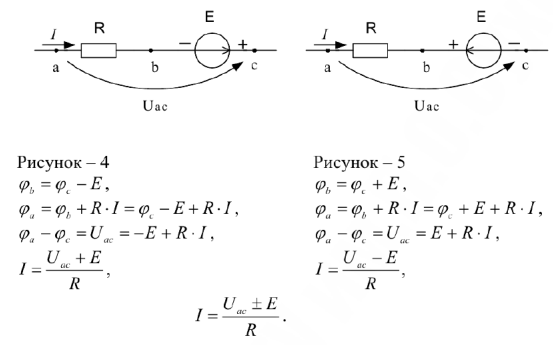
Первый закон Кирхгофа
Алгебраическая сумма токов в любом узле эл. цепи равна нулю, т.е. сумма токов втекающих в узел равна сумме токов вытекающих из него.
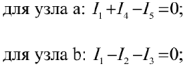
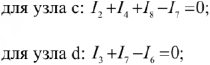
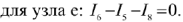
Второй закон Кирхгофа
Алгебраическая сумма падений напряжений в любом замкнутом контуре равна алгебраической сумме ЭДС входящих в этот контур.
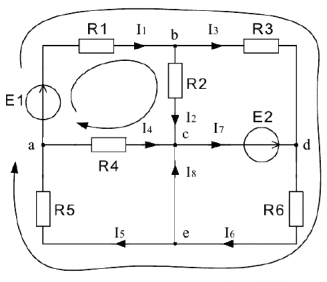
Произвольно выбираем УПН токов в элементах эл. цепи. УПН обхода контуров выбираем по часовой стрелке. Направление падения напряжения на пассивных элементах (сопротивлениях) совпадает с выбранным УПН токов, которые протекают в этих элементах. Напряжение на элементе записывается со знаком «+» если УПН тока в этом элементе совпадает с УПН обхода контура, в противном случае напряжение записывается со знаком «-».
Контур 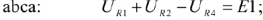
Контур 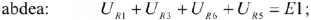
Эквивалентные преобразования в электрических цепях
Последовательное соединение элементов
Последовательным называется такое соединение элементов, когда условный конец первого элемента соединяется с условным началом второго, конец второго — с началом третьего и т.д.
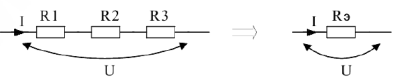
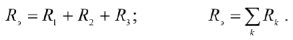
При последовательном соединении элементов их эквивалентное сопротивление равно сумме всех сопротивлений входящих в данное соединение.
Параллельное соединение элементов
Параллельным называется такое соединение элементов, при котором соединяются между собой как условные начала всех элементов. так и их концы.
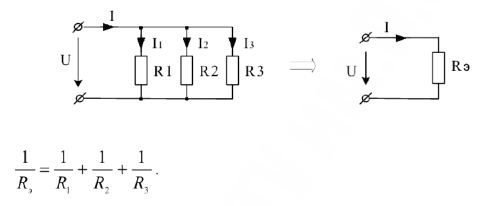
При параллельном соединении элементов их эквивалентная проводимость равна сумме всех проводимостсй элементов входящих в данное соединение.
Преобразование звезды в треугольник и обратное преобразование
Для упрощения анализа и расчета некоторых электрических цепей, содержащих соединения треугольником, целесообразно заменить их эквивалентными элементами, соединенными звездой. Примером подобных электрических цепей являются мостовые цепи.
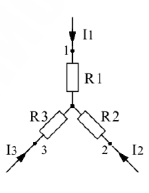
Из звезды в треугольник:
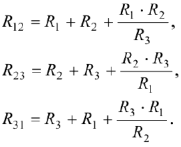
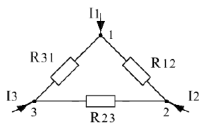
Из треугольника в звезду:
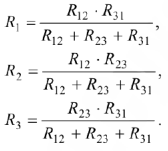
Методы расчета линейных электрических цепей. Электрические цени постом иного тока
Расчет электрической цепи может проводиться в форме анализа или синтеза цепи. Целью анализа является расчет эл. процессов в заданных цепях, когда известны структура (конфигурация, топология) цепи, параметры ее элементов и требуется определить токи, напряжения и мощность на определенных ее участках. Целью синтеза является обратная задача — определение структуры эл. цепи и характеристик се элементов при которых эл. процессы в цепи будут подчиняться заданным закономерностям или будет изменяться в желательном для нас направлении.
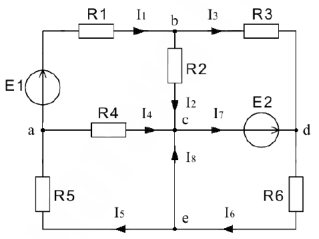
Метод уравнений Кирхгоффа
Известно: 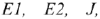
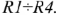
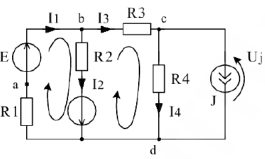
Определить реальные токи во всех ветвях цепи и проверить правильность расчета.
В данной схеме 4 неизвестных тока и 5 ветвей, в одной из которых источник тока. Произвольно задаем УПН токов в ветвях и напряжения источника тока. Число уравнений составляемых по законам Кирхгофа равно числу неизвестных. В данной схеме 3 узла, поэтому по первому закону составляем 2 уравнения, остальные уравнения составляем по второму уравнению.
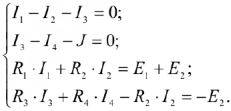
Решая данную систему, определяем реальные токи 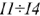 . Если значение тока получилось отрицательным — значит его направление противоположно VIII1. Напряжение на источнике тока можно найти но второму закону Кирхгофа:
. Если значение тока получилось отрицательным — значит его направление противоположно VIII1. Напряжение на источнике тока можно найти но второму закону Кирхгофа: 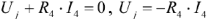 .
.
Порядок расчета:
- Анализ схемы с целью определения количества ветвей с неизвестными реальными токами и количества потенциальных узлов.
- Задание УПН неизвестных реальных токов.
- Составление уравнений по первому закону Кирхгофа. Их число должно быть равно количеству узлов минус 1.
- Недостающие уравнения составляем по второму закону Кирхгофа для независимых контуров. Желательно при составлении таких уравнений не рассматривать контуры, содержащие источник тока.
- Решая уравнения, определяем реальные токи
- Проверка расчета.
Проверку расчета в данном и остальных методах можно осуществить двумя путями: путем составления энергетического баланса (баланса мощносш), и путем построения потенциальной диаграммы.
Энергетический баланс составляется на основании закона о сохранении энергии, согласно которому энергия, выделившаяся в единицу времени в элементах схемы в виде тепла должна равняться энергии вырабатываемой ИИ за то же время. Чтобы исключить сомножитель времени считают баланс мощностей. Составим баланс мощности.
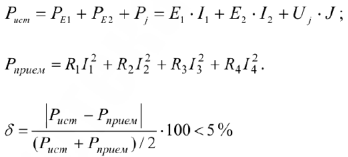
Если относительная ошибка менее 5%, то расчет можно считать правильным.
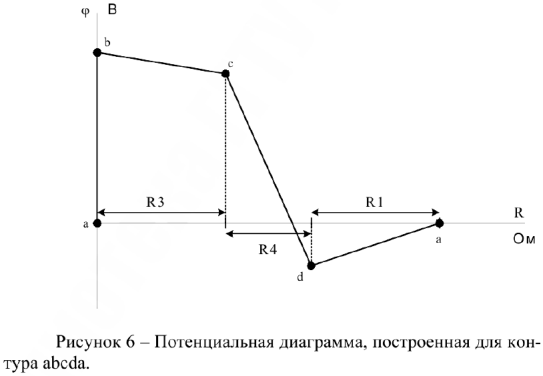
Потенциальная диаграмма — график изменения потенциала вдоль замкнутого контура или определенного участка цепи. Суть проверки в том, что мы выбираем одну точку либо узел контура и зануляем ее, т.е. считаем, что ее потенциал равен нулю. Далее обходим контур, поочередно находя потенциалы всех точек и узлов. В итоге мы придем к исходной точке (узлу) потенциал которой должен равняться выбранному, т.е. нулю. Обойдем контур 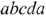 . Допустим пусть
. Допустим пусть 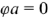 тогда:
тогда:
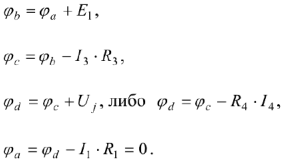
Частный случай МУК, когда сложная разветвленная цепь содержит лишь один ИП. Такие задачи решаются используя как правило эквивалентные преобразования эл. цепей.
Метод контурных токов
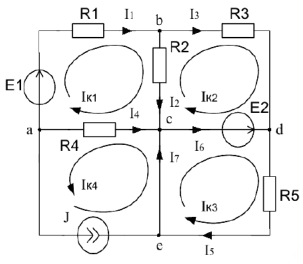
Известно: 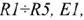
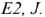
Определить все реальные токи.
Выберем УПН реальных токов. Составим уравнение по второму закону Кирхгофа для контура adca (контур будем обходить по часовой стрелке).
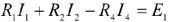
Выберем УПН контурных токов и запишем реальные токи 11,12,14 через контурные:
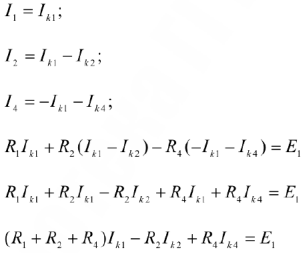
Проделывая аналогичные математические операции для остальных контуров можно получить систему уравнений:
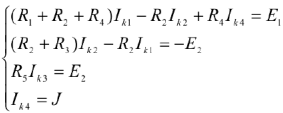
В общем случае мы получили систему из четырех уравнений, т.е. количество уравнений равно количеству независимых контуров пени. В данном случае систему можно упростить и уменьшить количество уравнений до трех.
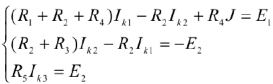
Решая систему, находим значения промежуточных неизвестных 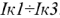 . Зная эти значения, реальные токи определяют следующим образом:
. Зная эти значения, реальные токи определяют следующим образом:
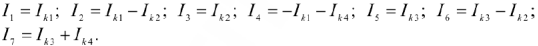
Решая данную задачу метом уравнений Кирхгофа нам потребовалось бы составить и решать систему из 7-ми уравнений. Порядок расчета:
- Анализ схемы.
- Выбор УПН реальных токов.
- Выбор УПН контурных токов протекающих в независимых контурах.
- Составление уравнений по второму закону Кирхгофа для независимых контуров цепи относительно контурных токов, причем количество уравнений равно количеству независимых контуров цепи.
- Решение системы и определение контурных токов.
- Определение реальных токов через контурные.
- Проверка расчета.
Второй пункт расчета допускается выполнять после пятого.
Метод узловых потенциалов
Известно, что ток в любой ветви схемы можно найти по закону Ома. Для этого надо знать потенциалы отдельных узлов схемы. Метод расчета, в котором в качестве промежуточных неизвестных применяются электрические потенциалы узлов, называется методом узловых потенциалов.
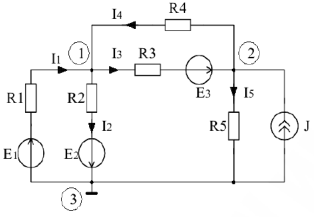
Известно: 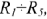
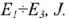
Определить все реальные токи. Будем считать, что потенциал узла 3 равен нулю 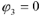 . По закону Ома запишем уравнения для реальных токов.
. По закону Ома запишем уравнения для реальных токов.
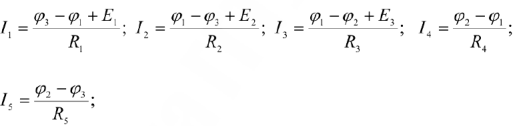
По первому закону Кирхгофа для 1-го и 2-го узлов запишем:
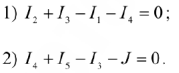
Далее, после подстановки получим:
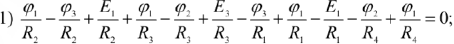
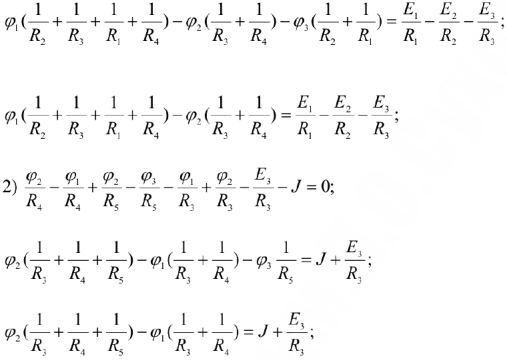
Решая два данных уравнения, определяем потенциалы 1-го и 2-го узлов. Учитывая, что 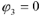 по закону Ома определяем реальные токи в ветвях цепи.
по закону Ома определяем реальные токи в ветвях цепи.
Порядок расчета:
- Анализ схемы.
- Заземление одного из узлов цепи (выполняется произвольно). Потенциал этого узла принимается равным нулю. Поэтому, число уравнений составленных относительно неизвестных узловых потенциалов равно количеству узлов без 1.
- Составляем систему уравнений относительно неизвестных узловых потенциалов.
- Решаем систему.
- По закону Ома определяем искомые реальные токи.
- Проверка расчета.
Метод наложения
Основой метода является принцип наложения (суперпозиции), который формулируется следующим образом: ток в любой ветви эл. цепи равен алгебраической сумме токов вызываемых в этой ветви каждым источником ЭДС или тока в отдельности.
Порядок расчета:
- Анализ схемы.
- Выбор УИН реальных токов в исходной схеме.
- Построение частных расчетных схем, каждая из которых содержит лишь один источник энергии. При построении частных схем следует помнить, что идеальный источник ЭДС закарачивают, а ветви с идеальным источником тока разрывают.
- Расчет каждой из схем любым методом (чаще всего пользуются методом свертывания).
- Определение искомых реальных токов путем алгебраического суммирования соответствующих частных токов.
- Проверка расчета.
Известно: 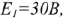
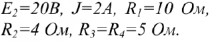
Определить все токи методом наложения. Выбираем УПН реальных токов. Так как исходная схема содержит 3 ИП, то частных расчетных схем будет также три.
Выбираем УПН для частных схем и находим неизвестные токи методом свертывания.
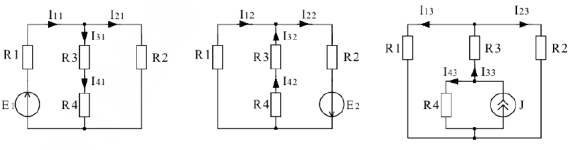
Для первой частной схемы
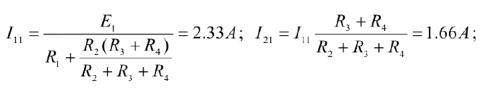
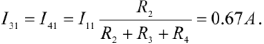
Для второй частной схемы
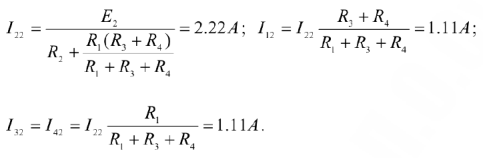
Для третьей частной схемы

Путем алгебраического суммирования соответствующих частных токов найдем реальные:
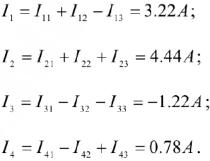
Проверить правильность расчета можно составлением баланса мощностей либо построением потенциальной диаграммы цени. Составим баланс мощностей.
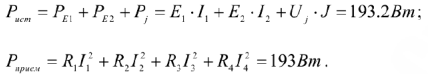
Расчет можно считать правильным т.к. относительная ошибка менее 5%.
Метод эквивалентного генератора
В основе метода лежит теорема об активном 2-х полюснике (эквивалентном генераторе). Согласно этой теореме по отношению к выделенной ветви оставшуюся сколь угодно сложную часть схемы можно заменить активным 2-х полюсником, ЭДС которого численно равна напряжению Х.Х. на зажимах выделенной ветви, а внутреннее сопротивление — входному (эквивалентному) сопротивлению оставшейся части цепи по отношению к зажимам выделенной ветви.
Поридок расчета:
- Анализ схемы.
- Построение частных схем для определения параметров эквивалентного генератора
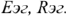
- Определение ЭДС эквивалентного генератора любым известным методом.
- Определение внутреннего сопротивления эквивалентного генератора. При этом идеальные источники ЭДС в оставшейся схеме закарачивают, а ветви с источником тока обрывают.
- По определенным значениям
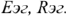 г рассчитывают ток в ветви по закону Ома.
г рассчитывают ток в ветви по закону Ома.
Метод эквивалентного генератора называется частным т.к. позволяет рассчитывать ток лишь в одной ветви. Методы уравнений Кирхгофа, свертывания, контурных токов, наложения, узловых потенциалов называют общими т.к. они позволяют рассчитывать токи во всех ветвях. Метод эквивалентного генератора применяют в основном, когда требуется выяснить режим работы конкретной ветви в зависимости от се сопротивления.
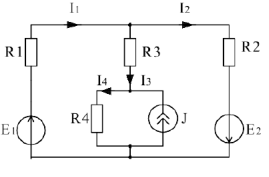
Известно:
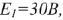
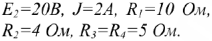
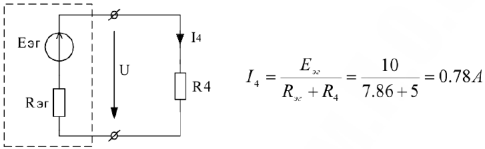
Определить 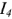 методом эквивалентного генератора.
методом эквивалентного генератора.
Строим частную схему для определения напряжения холостого хода на зажимах выделенной ветви.
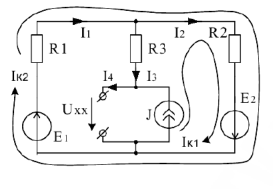
Напряжение Х.Х. определяем по второму закону Кирхгофа:
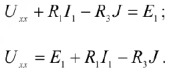
Неизвестный ток 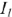 в данной схеме в режиме Х.Х можно определить любым известным методом, например, методом контурных токов.
в данной схеме в режиме Х.Х можно определить любым известным методом, например, методом контурных токов.
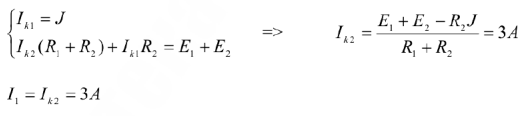
Подставляя значение 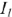 в исходное уравнение, находим значение напряжения Х.Х.
в исходное уравнение, находим значение напряжения Х.Х. 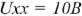 . Для определения внутреннего сопротивления эквивалентного генератора строим частную схему.
. Для определения внутреннего сопротивления эквивалентного генератора строим частную схему.
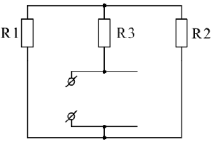
При построении частных схем для определения 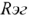 следует помнить, что идеальный источник ЭДС закарачивают, а ветви с идеальным источником тока разрывают. Итак, сопротивление оставшейся части цепи по отношению к зажимам выделенной ветви:
следует помнить, что идеальный источник ЭДС закарачивают, а ветви с идеальным источником тока разрывают. Итак, сопротивление оставшейся части цепи по отношению к зажимам выделенной ветви:
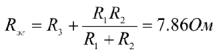
В результате мы заменили часть цепи активным 2-х полюсником.
Метод двух узлов
Метод двух узлов (метод узлового напряжения) даст возможность весьма просто произвести анализ и расчет электрической цепи, содержащей несколько параллельно соединенных активных и пассивных ветвей.
Известно:
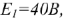
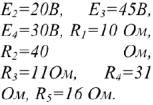
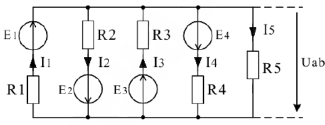
Определить все токи методом узлового напряжения.
Выбираем УПН токов и напряжения 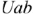 . Тогда по второму закону Кирхгофа для контура, проходящего по первой ветви:
. Тогда по второму закону Кирхгофа для контура, проходящего по первой ветви:
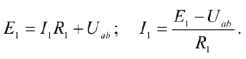
Аналогичным образом находим остальные токи. По первому закону Кирхгофа для узла 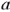 :
:
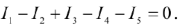
После замены токов и преобразования получим:
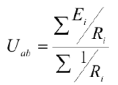
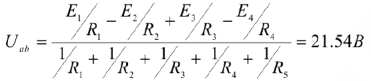
Определяем реальные токи в ветвях:
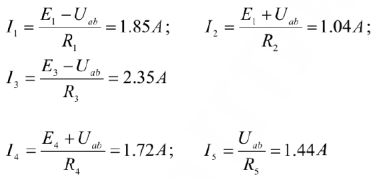
Порядок расчета:
- Анализ схемы.
- Выбор УИН токов и узлового напряжения. (Выбор У ГШ токов можно производить после выполнения п.З)
- Расчет узлового напряжения. Причем со знаком «+» должны входить ЭДС, направленные между узлами встречно узловому напряжению.
- Определение реальных токов.
- Проверка расчета.
Передача энергии в цепи постоянного тока
Нагрузка называется согласованной с источником, если ее сопротивление равно внутреннему сопротивлению ИП.
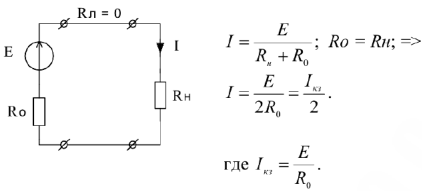
В согласованном режиме в нагрузке выделяется максимальная мощность:
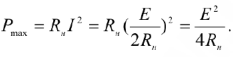
В том случае, когда внутренне сопротивление источника пренебрежимо мало, а сопротивление линии не равно нулю — схема передачи эл. эн. примет вид:
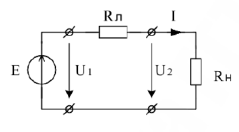
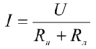
При изменении нагрузки 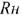 и постоянном напряжении
и постоянном напряжении 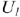 будет изменяться ток в цепи, мощность, выделяемая источником и потребляемая нагрузкой, а так же КПД электропередачи. Установим, как изменяется
будет изменяться ток в цепи, мощность, выделяемая источником и потребляемая нагрузкой, а так же КПД электропередачи. Установим, как изменяется 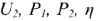 в зависимости от нагрузки или тока в цепи.
в зависимости от нагрузки или тока в цепи.
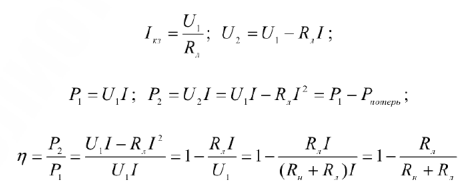

Электрические цепи однофазного синусоидального тока
Синусоидальный ток и его характеристики
В современной технике широко используют разнообразные по форме переменные токи и напряжения: синусоидальные, прямоугольные, треугольные и др. Значение тока, напряжения, ЭДС в любой момент времени 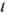 называется мгновенным значением и обозначается малыми строчными буквами, соответственно
называется мгновенным значением и обозначается малыми строчными буквами, соответственно
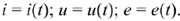
Токи, напряжения и ЭДС, мгновенные значения которых повторяются через равные промежутки времени, называют периодическими, а наименьший промежуток времени, через который эти повторения происходят, называют периодом 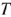 .
.
Если кривая изменения периодического тока описывается синусоидой. то ток называют синусоидальным. Если кривая отличается от синусоиды, то ток нссинусоидальный.
При расчете и анализе электрических цепей применяют несколько способов представления синусоидальных электрических величин.
Аналитический способ
Для тока
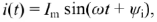
для напряжения
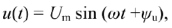
для ЭДС
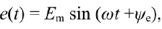
- где
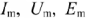 — амплитуды тока, напряжения, ЭДС; значение в скобках — фаза (полная фаза);
— амплитуды тока, напряжения, ЭДС; значение в скобках — фаза (полная фаза); 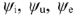 — начальная фаза тока, напряжения, ЭДС;
— начальная фаза тока, напряжения, ЭДС; 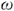 — циклическая частота,
— циклическая частота, 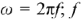 — частота,
— частота, 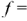
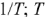 ; — период.
; — период.
Частота  измеряется в герцах (Гц), циклическая частота со имеет размерность рад/с. Значения начальных фаз
измеряется в герцах (Гц), циклическая частота со имеет размерность рад/с. Значения начальных фаз 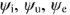 могут измеряться в радианах или градусах. Величина
могут измеряться в радианах или градусах. Величина 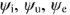 зависит от начала отсчета времени
зависит от начала отсчета времени 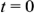 . На временных диаграммах положительное значение откладывается влево, отрицательное — вправо.
. На временных диаграммах положительное значение откладывается влево, отрицательное — вправо.
Временная диаграмма
Временная диаграмма представляет графическое изображение синусоидальной величины в заданном масштабе в зависимости or времени (рис. 8).
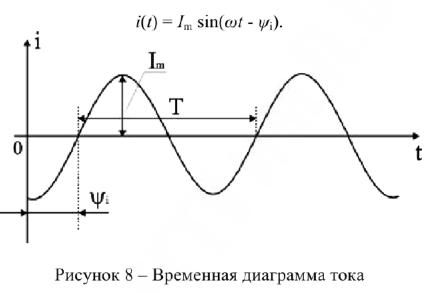
Графоаналитический способ
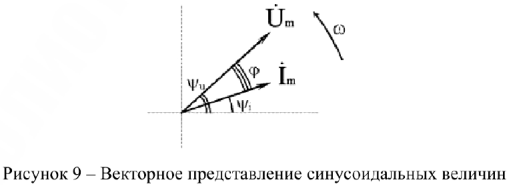
Графически синусоидальные величины изображаются в виде вращающегося вектора (рис. 9). Предполагается вращение против часовой стрелки с частотой вращения 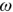 . Величина вектора в заданном масштабе представляет амплитудное значение. Проекция на вертикальную ось есть мгновенное значение величины.
. Величина вектора в заданном масштабе представляет амплитудное значение. Проекция на вертикальную ось есть мгновенное значение величины.
Совокупность векторов, изображающих синусоидальные величины (ток, напряжение, ЭДС) одной и той же частоты называют векторной диаграммой.
Векторные величины отмечаются точкой над соответствующими переменными.
Использование векторных диаграмм позволяет существенно упросить анализ цепей переменного тока, сделать его простым и наглядным.
Среднее и действующее значение синусоидально изменяющихся величин
Среднее значение тока (ЭДС, напряжения) — это среднее арифметическое значение тока (ЭДС, напряжения) за интервал времени. Для синусоидальных величин в качестве интервала времени выбирают половину периода, т.е., т.к. среднее значение синусоидальной величины за период равно нулю. Среднее значение синусоидального тока
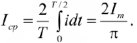
Для оценки синусоидально изменяющихся величин нельзя применять их средние значения, так как среднее за период значение любой синусоидальной величины равно нулю. В качестве оценки этих величин вводится так называемое действующее значение тока, э.д.с. или напряжения
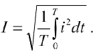
Если переменная величина, в данном случае ток изменяется по синусоидальному закону, то
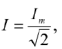
то есть действующее значение тока равно максимальному, деленному на корень из двух.
Главное преимущество действующего значения синусоидально изменяющейся величины в том. что оно не зависит от времени, следовательно, его удобно изображать на графиках, с его помощью легко проводить всевозможные расчеты. Большинство электроизмерительных приборов сконструировано так, что они фиксируют именно действующие значения синусоидальных токов и напряжений.
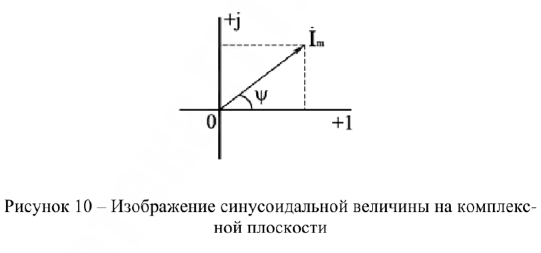
Изображение синусоидально изменяющихся величин векторами на комплексной плоскости
Синусоидальный ток 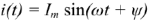 можно представить комплексным числом
можно представить комплексным числом 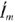 на комплексной плоскости (рис. 10)
на комплексной плоскости (рис. 10)
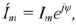
где амплитуда тока 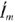 — модуль, а угол
— модуль, а угол 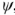 , являющийся начальной фазой, — аргумент комплексного тока.
, являющийся начальной фазой, — аргумент комплексного тока.
Переменная в комплексной форме обозначается либо точкой, которая ставится над символом переменной либо знаком подчеркивания, который ставится под символом переменной. Например, комплексное значение тока можно обозначать 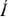 или
или 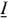 .
.
Использование комплексной формы представления позволяет заменить геометрические операции над векторами алгебраическими операциями над комплексными числами. В результате этого к анализу цепей переменного тока могут быть применены все методы анализа цепей постоянного тока.
Операции с комплексными числами
Сложение
Сложение комплексных чисел осуществляется в алгебраической форме и определяется следующим образом: суммой чисел 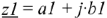 и
и 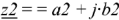 является число
является число
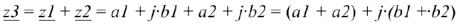
Т.е. выполняется непосредственное суммирование действительных и мнимых частей.
Вычитание
Вычитание комплексных чисел также осуществляется в алгебраической форме. Разность двух чисел 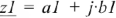 и
и 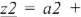
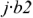 является число
является число
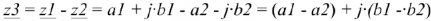
Таким образом, чтобы вычесть из одного числа другое, выполняется непосредственное вычитание действительных и мнимых частей.
Деление
Частное комплексных чисел в показательной форме 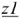
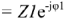 и
и 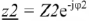 находится путем деления модулей и вычитания начальных фаз комплексных чисел:
находится путем деления модулей и вычитания начальных фаз комплексных чисел:
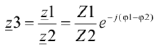
Умножение
Произведение комплексных чисел в показательной форме 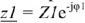 и
и 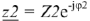 находится путем перемножения модулей и сложения начальных фаз комплексных чисел:
находится путем перемножения модулей и сложения начальных фаз комплексных чисел:
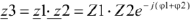
Простейшие элементы в цепи переменного тока
Индуктивные катушки и конденсаторы оказывают сопротивление протекающим по ним переменным токам. В этих сопротивлениях не происходит превращения электрической энергии в тепловую. Поэтому в отличие от активных сопротивлений их называют реактивными. Реактивное сопротивление индуктивной катушки называется индуктивным сопротивлением, обозначается 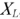 , и вычисляется по формуле:
, и вычисляется по формуле:
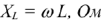
где 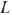 — индуктивность катушки, Г (генри).
— индуктивность катушки, Г (генри).
Реактивное сопротивление конденсатора называется емкостным сопротивлением, обозначается 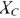 и вычисляется по формуле:
и вычисляется по формуле:
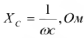
где 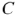 — емкость конденсатора в фарадах.
— емкость конденсатора в фарадах.
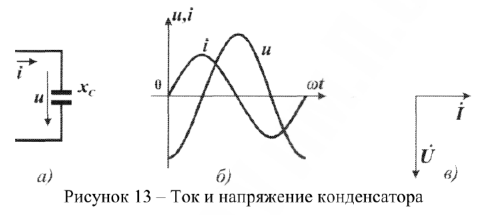
В активном сопротивлении напряжение совпадает с током по фазе. Если ток, текущий по сопротивлению на рисунке 11, а задан выражением
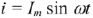
то напряжение на этом сопротивлении изменяется по закону:
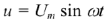
Синусоиды тока и напряжения, а также их векторная диаграмма представлена на рис. 11. б, в.
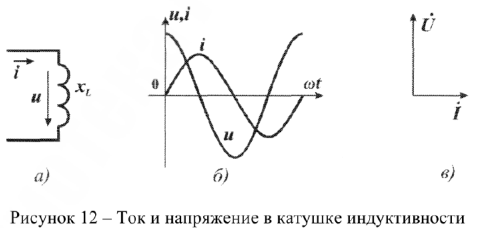
В катушке индуктивности напряжение опережает ток по фазе на угол 90°. Если ток катушки задан выражением:
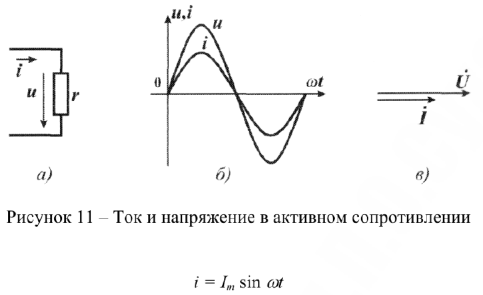
то напряжение на катушке изменяется по закону:
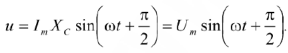
Схема цепи, синусоиды тока и напряжения, также их векторная диаграмма приведены на рисунке 12.
В конденсаторе напряжение отстает от тока по фазе на угол 90°. Если ток. протекающий через конденсатор, задан выражением:
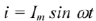
то напряжение на конденсаторе изменяется по закону:
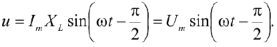
Схема цепи, синусоиды тока и напряжения, а также их векторная диаграмма приведены на рисунке 13.
Расчет цепей однофазною синусоидальною тока в комплексной форме
Расчет цепей синусоидального тока в общем случае связан с решением неоднородных дифференциальных уравнений, составленных по законам Кирхгофа относительно мгновенных значений токов и напряжений. Решение таких уравнений является громоздким и трудоемким.
На практике широкое распространение получил символический метод расчета, сущность которого состоит в том, что действительные синусоидальные функции времени заменяют соответствующими комплексными числами. В результате уравнения становятся алгебраическими с комплексными коэффициентами.
Расчет ЭЦ символическим методом производится в следующем порядке:
- от переменных заданных в гармонической форме переходят к комплексным изображениям;
- с помощью любого известного метода расчета определяют комплексные токи и напряжения (реакция цепи);
- от комплексных изображений токов и напряжений переходят к их мгновенным значениям.
Пример: Составить уравнения по MKT и МУН для схемы рис. 14.
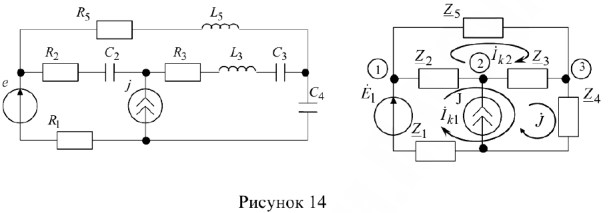
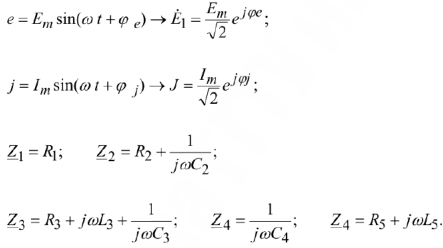
Метод контурных токов
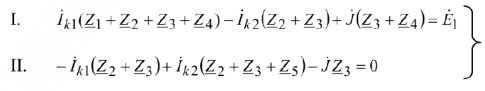
Метод узловых напряжений (метод узловых потенциалов)
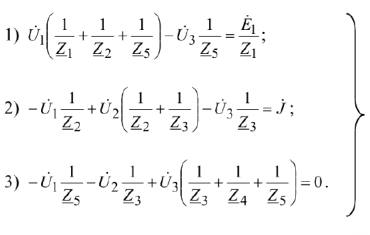
Выражение мощности в комплексной форме. Баланс мощностей
Под комплексной мощностью понимается величина, определяемая по формуле
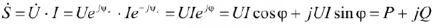
где 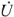 — комплексное действующее значение напряжения;
— комплексное действующее значение напряжения; 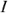 — сопряженный комплексный ток.
— сопряженный комплексный ток.
Вещественная часть комплексной мощности равна активной мощности 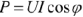 (измеряется в Вт), мнимая часть — реактивной мощности
(измеряется в Вт), мнимая часть — реактивной мощности 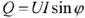 (измеряется в ВАр). Модуль комплексной мощности равен полной мощности
(измеряется в ВАр). Модуль комплексной мощности равен полной мощности 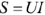 (измеряется в ВА).
(измеряется в ВА).
Связь между активной, реактивной и полной мощностями
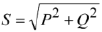
Из закона сохранения энергии следует, что в любой электрической цепи соблюдается баланс как мгновенных, так и активных мощностей:
Сумма отдаваемых источниками мгновенных (активных) мощностей равна сумме потребляемых цепью мгновенных (активных) мощностей. Баланс выполняется также для реактивных и для комплексных мощностей, т.е.
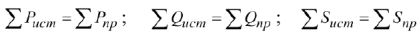
Резонанс в электрических цепях
Резонансом в электрической цепи называется режим участка, содержащего индуктивный и емкостный элементы, при котором угол 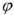 сдвига фаз колебаний напряжения и тока равен нулю. Резонанс характеризуется рядом особенностей, которые обусловили его широкое применение в радиотехнике, электротехнике, измерительной технике и других областях.
сдвига фаз колебаний напряжения и тока равен нулю. Резонанс характеризуется рядом особенностей, которые обусловили его широкое применение в радиотехнике, электротехнике, измерительной технике и других областях.
Различаю! несколько видов резонанса: резонанс напряжений (при последовательном соединении элементов), резонанс токов (при параллельном соединении элементов), резонанс в магнитно-связанных цепях и др.
Резонанс напряжений возникает при последовательном соединении 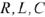 ток в цепи приобретает максимальное значение при
ток в цепи приобретает максимальное значение при 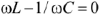 , то есть при
, то есть при 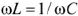 . Этому условию удовлетворяет частота
. Этому условию удовлетворяет частота
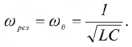
- В этом случае
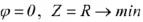 , падения напряжения на катушке индуктивности и конденсаторе одинаковы по величине и противоположны по фазе. Таким образом, при резонансе напряжений
, падения напряжения на катушке индуктивности и конденсаторе одинаковы по величине и противоположны по фазе. Таким образом, при резонансе напряжений
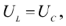
и
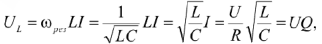
где 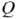 — добротность контура.
— добротность контура.
Так как добротность колебательных контуров больше единицы, то напряжение, как на катушке индуктивности, так и на конденсаторе превышает напряжение 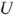 , приложенное к цепи. Добротность контура показывает, во сколько раз при резонансе напряжение на реактивных элементах больше по величине входного напряжения.
, приложенное к цепи. Добротность контура показывает, во сколько раз при резонансе напряжение на реактивных элементах больше по величине входного напряжения.
Явление резонанса напряжений используется в радиотехнике и электронике для усиления колебаний напряжения какой-либо определенной частоты. В электроэнергетике явление резонанса напряжений необходимо учитывать при выборе изоляции высоковольтного оборудования, так как иначе может произойти ее пробой.
Трехфазные цепи
Трехфазная система ЭДС
Трехфазная система состоит из трех источников электроэнергии и трех цепей, соединенных общими проводами линии передачи.
Источником энергии для всех фаз системы является трехфазный генератор у которою на статоре размешены три изолированные друг от друга одинаковые обмотки. Они расположены так, чтобы индуктируемые в них э.д.с. были сдвинуты по фазе одна относительно другой на 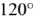 .
.
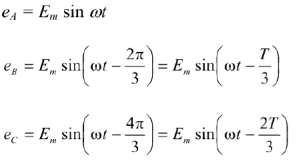
На схемах трехфазные источники изображают так, как показано на рис.15.
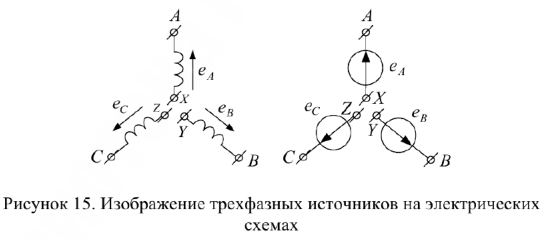
За условно положительное напряжение ЭДС в каждой фазе принимают направление от конца 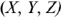 к началу
к началу 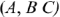 .
.
Система ЭДС, имеющих одинаковые амплитуды и сдвинуты по фазе друг относительно друга на один и тот же угол (120 электрических градусов) называется симметричной.
Основные схемы соединения трехфазных цепей
Приемники, включаемые в трехфазную цепь, могут быть как однофазными, так и трехфазными.
Трехфазные приемники, в свою очередь, подразделяются на симметричные и несимметричные.
Симметричными называют приемники, комплексы сопротивлений фаз которых равны между собой:
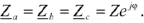
Если данное условие не выполняется, то приемники называют несимметричными. При этом нагрузка может быть равномерной или однородной.
В случае равномерной нагрузки
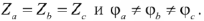
В случае однородной нагрузки
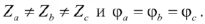
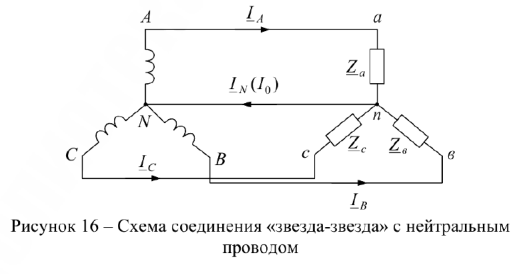
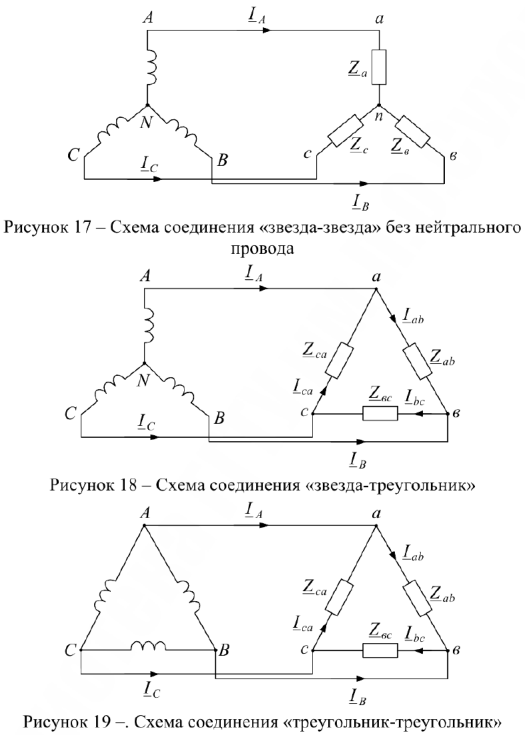
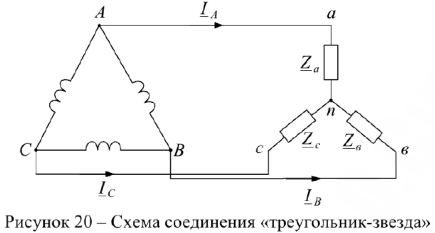
На практике применяются различные комбинации соединений нагрузки и трехфазного источника питания. Наиболее распространенные комбинации приведены на рис. 16-20.
Определение линейных и фазных величин
Текущие по линейным проводам токи принято называть линейными, их обозначают 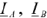 и
и 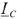 . За положительное направление линейных токов принимают их направление от генератора к нагрузке.
. За положительное направление линейных токов принимают их направление от генератора к нагрузке.
Напряжения между началом и конном каждой фазы источника называют фазными и обозначают 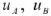 и
и 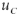 . Напряжения между одноименными выводами разных фаз называют, в свою очередь, линейными и обозначают
. Напряжения между одноименными выводами разных фаз называют, в свою очередь, линейными и обозначают 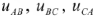 (рис. 21).
(рис. 21).
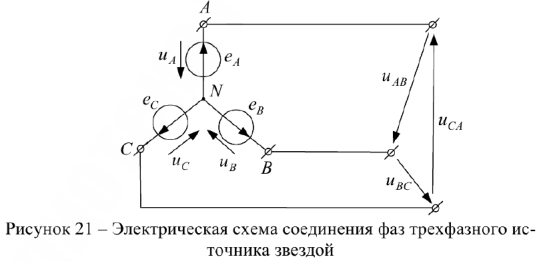
За условное положительное направление фазных напряжений принимают направление от начала к концу фаз обмотки, а линейных напряжений — от начала любой фазы к началу отстающей фазы.
Соотношения между линейными и фазными напряжениями и токами
Векторная топографическая диаграмма напряжений трехфазного источника при соединении его фаз звездой приведена на рис.22.
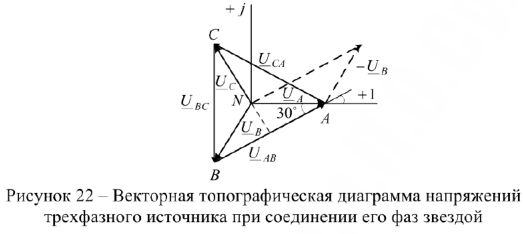
Из векторной диаграммы (рис. 22) видно, что векторы линейных напряжений сдвинуты друг относительно друга на угол 120°. Кроме того, векторы линейных напряжений 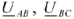 и
и 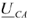 опережают соответствующие векторы фазных напряжений
опережают соответствующие векторы фазных напряжений 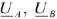 и
и 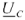 на угол 30°.
на угол 30°.
Величина каждого из векторов линейных напряжений в 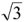 раз больше величины вектора фазного напряжения, т.е.
раз больше величины вектора фазного напряжения, т.е.
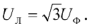
При соединении трехфазного источника треугольником фазные напряжения равны линейным, т.е. 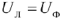 .
.
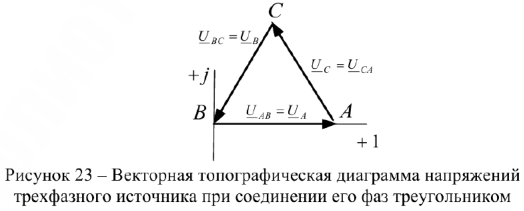
Расчет трехфазных цепей
Рассмотрим расчет трехфазной сети при соединении фаз генератора и нагрузки звездой. Схема соединения приемника звездой представлена на рис. 24.
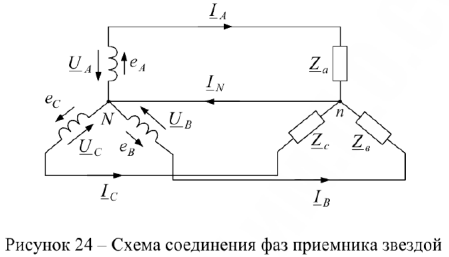
Если пренебречь сопротивлениями линейных н нейтрального проводов, то, очевидно, фазные напряжения приемника будут равны фазным напряжениям источника
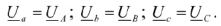
Тогда токи в каждой фазе приемника можно определить по формулам
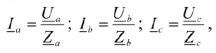
а ток в нейтральном проводе
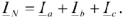
Из схемы видно, что при соединении фаз приемника звездой фазные и линейные токи равны между собой, т.е.
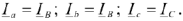
При симметричной нагрузке токи в фазах равны по величине и сдвинуты по фазе на один и тот же угол относительно соответствующих фазных напряжений. Векторная диаграмма напряжений и токов при симметричной нагрузке имеет вид, представленный на рис. 25.
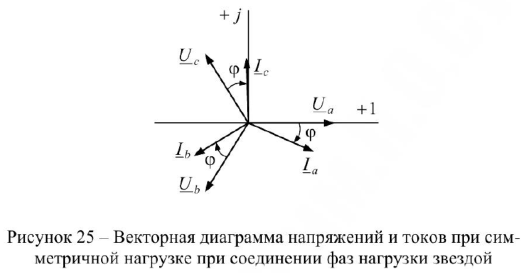
Из диаграммы следует, что 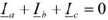 , т.е. при симметричной нагрузке ток в нейтральном проводе отсутствует
, т.е. при симметричной нагрузке ток в нейтральном проводе отсутствует 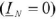 и необходимость в нейтральном проводе отпадает.
и необходимость в нейтральном проводе отпадает.
Таким образом, в общем случае при соединении звездой симметричных (трехфазных) приемников
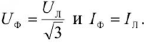
Для определения токов при симметричной нагрузке достаточно определить ток только в одной из фаз, входящих в трехфазную цепь.
Энергетический баланс в трехфазных электрических цепях
Пользуясь комплексной формой записи мощности, полную мощность трехфазного источника электрической энергии можно записать в виде:
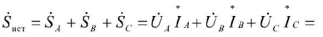
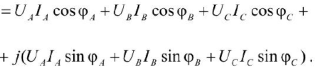
где 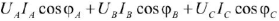 — активная мощность трехфазного источника;
— активная мощность трехфазного источника;
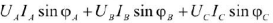 — реактивная мощность трехфазного источника.
— реактивная мощность трехфазного источника.
В свою очередь, активная и реактивная мощности, потребляемые трехфазными приемниками
при соединении фаз приемника звездой
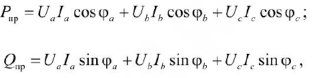
при соединении фаз приемника треугольником
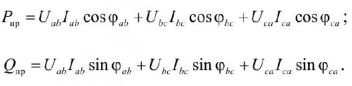
В частном случае симметричной нагрузки, фазы которой соединены звездой
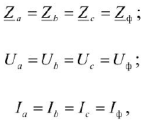
будем иметь:
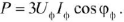
Данная формула справедлива не только для приемника фазы которого соединены звездой, но и для приемника фазы которого соединены треугольником.
Выразим фазные напряжения и токи через линейные напряжения и токи.
Для соединения приемника треугольником
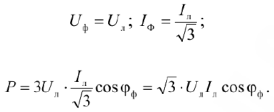
Для соединения звездой
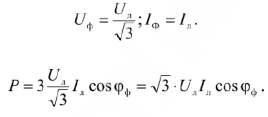
Таким образом, независимо от схемы соединения фаз приемника активная мощность при симметричной нагрузке определяется одной и той же формулой
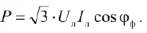
Аналогично реактивную и полную мощности приемника можно записать в виде
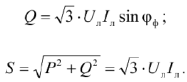
Из закона сохранения энергии следует, что в любой электрической цепи соблюдается баланс как мгновенных, так и активных мощностей:
Сумма отдаваемых трехфазным источником мгновенной (активных) мощностей равна сумме потребляемых цепью мгновенных (активных) мощностей. Баланс выполняется также для реактивных и для комплексных мощностей, т.е.
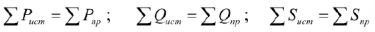
Измерение активной и реактивной мощности в трехфазных электрических цепях
Активную мощность, потребляемую трехфазными приемниками можно измерить с помощью однофазных ваттметров электродинамической или фсрродинамической систем.
Способ включения однофазных ваттметров для измерения активной мощности зависит or характера нагрузки (симметричная или несимметричная) и от числа проводов цепи.
Если трехфазный симметричный приемник соединен звездой без нейтрального провода (рис.26), то для измерения его активной мощности достаточно измерить активную мощность одной из фаз по схеме, и далее показание ваттметра умножить на три, т.е.
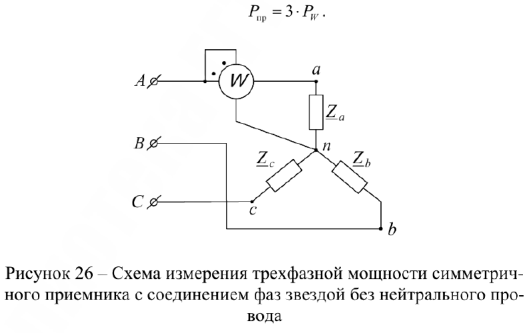
Однако не всегда имеется доступ к нейтральной точке приемника. В этом случае иногда используют схему измерения активной мощности с искусственной нейтральной точкой (рис.27). В этом случае
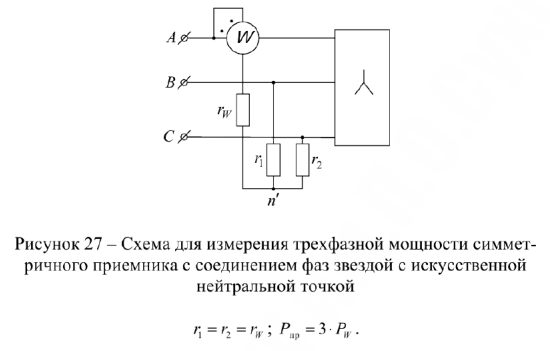
При соединении трехфазного симметричного приемника треугольником ваттметр следует включать как показано на рис.28. При этом
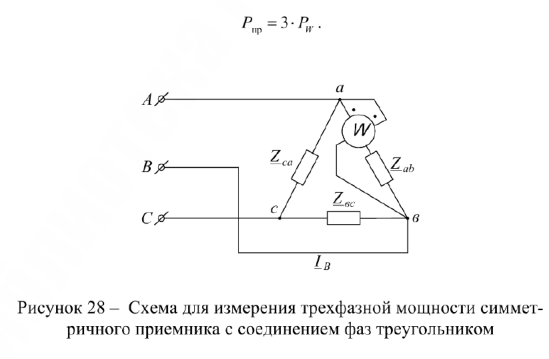
В четырехпроводной трехфазной цепи с несимметричной нагрузкой активную мощность можно измерить тремя ваттметрами. Каждый из них измеряет активную мощность отдельной фазы (рис.29).
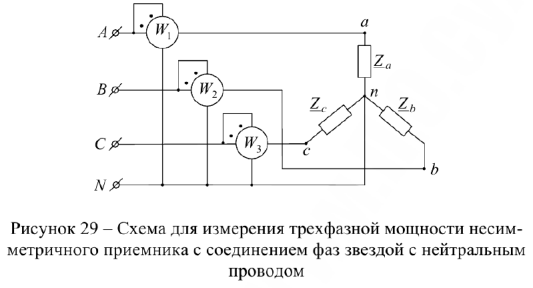
В этом случае
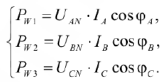
Активная мощность приемника (рис.29) будет складываться из суммы показаний каждого ваттметра
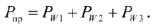
В трехпроводной трехфазной цепи активную мощность чаще всего измеряют методом двух ваттметров.
В общем случае мгновенная активная мощность
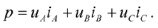
При соединении фаз приемника звездой
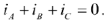
Выразив один из токов, например 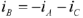 и подставив полученное значение в уравнение для мгновенной мощности, получим
и подставив полученное значение в уравнение для мгновенной мощности, получим
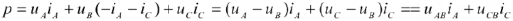
Перейдя к активной мощности, выраженной через действующие значения напряжений и токов, получим
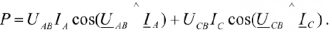
Учитывая это, изобразим схему включения ваттметров (рис.30.а).
Возможны еще два варианта включения двух ваттметров в трехфазную цепь (рис.З0.б-З0.в)
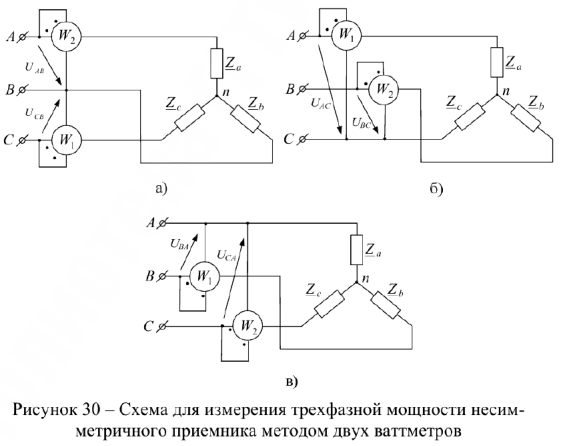
Нумерация ваттметров в схемах (рис.30) определяется порядком включения их токовых обмоток в линейные провода в соответствии с прямой последовательностью фаз  .
.
Векторная диаграмма токов и напряжений в случае симметричной нагрузки для схемы рис.30.а, соединенной звездой, представлена на рис.31.
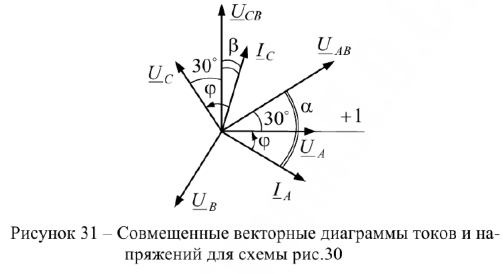
Из векторных диаграмм видно, что
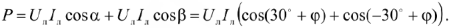
При 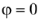 (т.е. при активной нагрузке) показания ваттметров будут одинаковы, а при
(т.е. при активной нагрузке) показания ваттметров будут одинаковы, а при 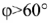 показания одного ваттметра станут отрицательными.
показания одного ваттметра станут отрицательными.
Это возможно потому, что показания одного ваттметра в рассматриваемой схеме (рис.ЗО.а) не имеют физического смысла.
Таким образом, активная мощность, измеренная методом двух ваттметров по схемам (рис.30), равна алгебраической сумме их показаний
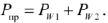
Метод двух ваттметров пригоден для измерений при симметричной и несимметричной нагрузках, при любом способе соединения приемников в трехпроводной цепи.
Реактивная мощность в трехпроводной трехфазной цепи при симметричной нагрузке может быть измерена одним ваттметром, включенным по схеме рис.32. Векторные диаграммы для этого случая представлены на рис.33.
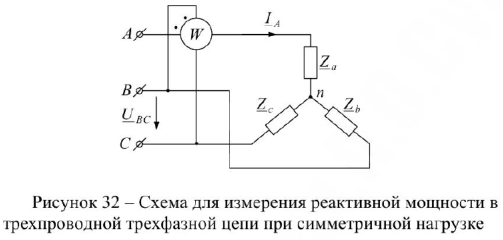
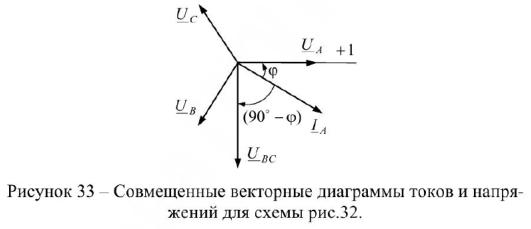
Показание ваттметра в схеме рис.32
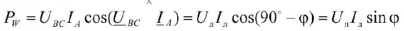
Известно также, что реактивная мощность приемника
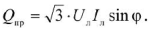
Следовательно,
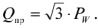
Реактивную мощность при симметричной нагрузке можно определить иначе, воспользовавшись показаниями ваттметров в схеме двух ваттметров.
В этом случае, согласно векторным диаграммам рис.31, разность между показаниями ваттметров равна
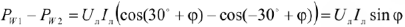
Таким образом,
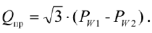
Наконец, но показаниям двух ваттметров можно определить характер симметричной нагрузки и ее коэффициент мощности
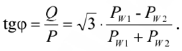
Нелинейные электрические цепи
Методы расчет нелинейных пеней постоянного тока
Электрическое состояние нелинейных цепей описывается на основании законов Кирхгофа, которые имеют общий характер. При этом следует помнить, что для нелинейных цепей принцип наложения неприменим. В этой связи методы расчета, разработанные для линейных схем на основе законов Кирхгофа и принципа наложения, в общем случае не распространяются на нелинейные цепи.
Общих методов расчета нелинейных цепей не существует. Известные приемы и способы имеют различные возможности и области применения.
На практике чаще имеется экспериментально снятая ВАХ нелинейного элемента. В таком случае для расчета можно применять графический метод. Таким образом, для расчета нелинейных цепей могут применяться графические, итерационные и аналитические методы.
Графические методы отличаются своей наглядностью. При этом достигаемый результат имеет точность, которая в большинстве случаев удовлетворяет предъявленным требованиям.
Решение нелинейных задач с помощью последовательных приближений состоит в разумном выборе предположительного решения и последовательного исправления результата. Правда, этот метод достаточно трудоемок и в большинстве случаев не нагляден.
Аналитические методы также мало наглядны. Они основаны на более или менее точной аппроксимации нелинейной зависимое!и и отличаются большой трудоемкостью, а точность в большинстве случаев может быть не выше, чем при графических методах. При расчетах аналитическим методом используют величины статических и дифференциальных сопротивлений нелинейного элемента.
Анализ различных методов расчета нелинейных цепей постоянного тока показывает, что графический метод для практики является более предпочтительным.
Последовательное соединение нелинейных элементов
Схема замещения рассматриваемой цепи приведена на рис. 34. Определить ток в цепи и напряжения на НЭ 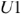 и
и 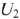 , если заданы входное напряжение
, если заданы входное напряжение 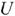 и ВАХ каждого элемента (рис. 35, а и б).
и ВАХ каждого элемента (рис. 35, а и б).
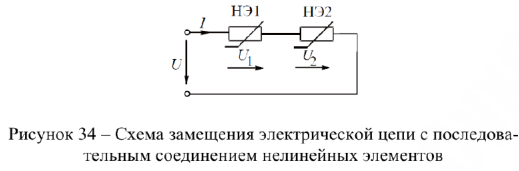
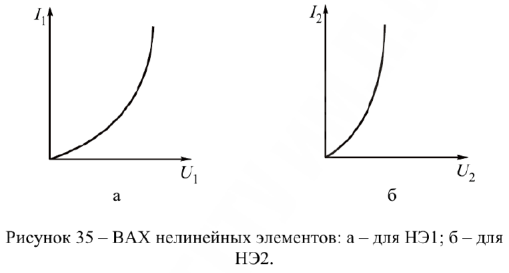
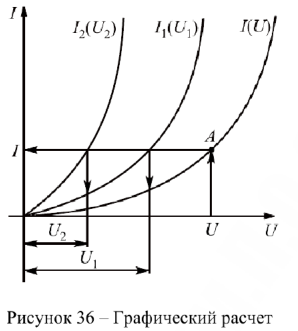
Ток в цепи один. Входное напряжение на основании второго закона Кирхгофа складывается из напряжений на отдельных НЭ. В рассматриваемой цепи 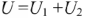 . Поэтому для построения результирующей ВАХ нужно при одном значении тока суммировать напряжения на нелинейных элементах. Чем больше точек будет получено, тем точнее результирующая ВАХ.
. Поэтому для построения результирующей ВАХ нужно при одном значении тока суммировать напряжения на нелинейных элементах. Чем больше точек будет получено, тем точнее результирующая ВАХ.
По заданному значению входного напряжения находим рабочую точку 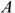 на результирующей ВАХ (рис. 36) и соответствующее ей значение тока. По полученному значению тока находим напряжения на отдельных элементах
на результирующей ВАХ (рис. 36) и соответствующее ей значение тока. По полученному значению тока находим напряжения на отдельных элементах 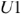 и
и 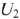 .
.
Параллельное соединение нелинейных элементов
Схема замещения рассматриваемой цепи приведена на рис. 37. Определить входной ток 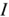 и токи
и токи 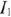 и
и 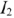 , если заданы входное напряжение и В АХ каждого нелинейного элемента (см. рис. 38, а и 6).
, если заданы входное напряжение и В АХ каждого нелинейного элемента (см. рис. 38, а и 6).
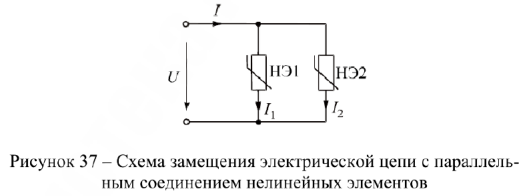
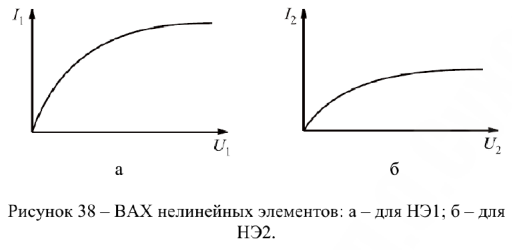
Так как при параллельном соединении напряжения на элементах одинаковы и равны входному 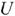 , то па ВАХ отдельных элементов находим токи
, то па ВАХ отдельных элементов находим токи 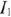 и
и 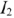 Входной ток на основании первого закона Кирхгофа равен сумме токов в пассивных ветвях:
Входной ток на основании первого закона Кирхгофа равен сумме токов в пассивных ветвях:
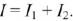
Если в анализируемой цепи нужно найти токи 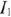 и
и 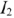 , а также входное напряжение при заданном входном токе, то рабочую точку можно найти на результирующей ВАХ.
, а также входное напряжение при заданном входном токе, то рабочую точку можно найти на результирующей ВАХ.
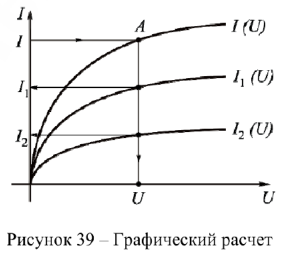
Для ее построения нужно при ряде одинаковых значений напряжения складывать токи 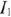 и
и 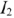 (рис. 39). По заданному значению тока
(рис. 39). По заданному значению тока 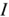 находим рабочую точку
находим рабочую точку 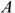 и соответствующее ей значение входного напряжения
и соответствующее ей значение входного напряжения 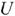 . По полученному значению напряжения
. По полученному значению напряжения 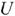 находим токи
находим токи 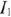 и
и 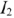 .
.
Расчет разветвленной нелинейной цепи
Схема замещения рассматриваемой цепи приведена па рис. 40.
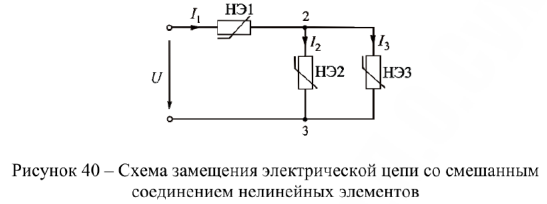
Определить все токи, сели задано входное напряжение и ВАХ отдельных элементов: 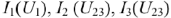 .
.
Решение заключается в постепенном построении результирующих ВАХ. Очевидно, что сначала нужно построить результирующую ВАХ для параллельного участка (для ряда значений напряжения 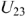 суммировать токи
суммировать токи 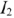 и
и 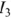 ). После этого схема превратится в последовательное соединение НЭ1 и эквивалентного элемента с ВАХ
). После этого схема превратится в последовательное соединение НЭ1 и эквивалентного элемента с ВАХ 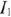 (
(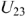 ), так как
), так как 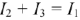 . Затем нужно построить результирующую ВАХ всей схемы. Для этого при ряде значений тока
. Затем нужно построить результирующую ВАХ всей схемы. Для этого при ряде значений тока 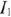 нужно суммировать напряжения
нужно суммировать напряжения 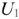 и
и 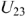 .
.
По заданному значению входного напряжения 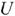 найдем рабочую точку и соответствующее ей значение входного тока
найдем рабочую точку и соответствующее ей значение входного тока 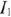 . Далее по графику
. Далее по графику 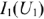 найдем напряжение
найдем напряжение 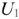 и определим напряжение
и определим напряжение 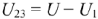 . По графикам
. По графикам 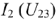 и
и 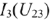 найдем токи
найдем токи 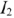 и
и 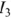 .
.
Расчет нелинейных ценен методом эквивалентною генератора
Этот метод можно использовать для схемы с одним нелинейным элементом, ток в котором и надо найти (рис. 41, а). Делим схему па две части: НЭ и всю остальную часть схемы, которая является активным двухполюсником (рис. 41, в).
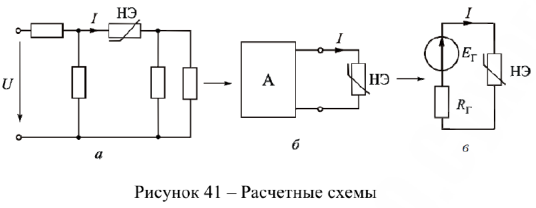
Активный двухполюсник заменим эквивалентным ему генератором (рис. 41, в). Активный двухполюсник является линейной цепью, расчет которой намного проще, чем нелинейной. ЭДС генератора 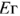 равна напряжению холостого хода на зажимах активного двухполюсника. Сопротивление
равна напряжению холостого хода на зажимах активного двухполюсника. Сопротивление 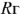 — это эквивалентное сопротивление пассивного двухполюсника относительно входных зажимов. Пассивный двухполюсник получаем из активного, закорачивая источники ЭДС и разрывая источники тока. Полученная схема (рис. 41, в) представляет собой последовательное соединение нелинейного и линейного элементов.
— это эквивалентное сопротивление пассивного двухполюсника относительно входных зажимов. Пассивный двухполюсник получаем из активного, закорачивая источники ЭДС и разрывая источники тока. Полученная схема (рис. 41, в) представляет собой последовательное соединение нелинейного и линейного элементов.
Рабочую точку рационально найти на пересечении ВАХ Н’Э и зеркального изображения ВАХ линейного элемента (рис. 42). График  является прямой линией, зеркально отображающей график
является прямой линией, зеркально отображающей график 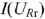 , смещенный вправо на величину
, смещенный вправо на величину 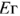 . Для его построения нужны две точки. Одна из них с координатами (
. Для его построения нужны две точки. Одна из них с координатами (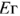 , 0). Для построения второй точки можно задаться нулевым значением тока либо любым произвольным
, 0). Для построения второй точки можно задаться нулевым значением тока либо любым произвольным 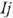 , для которого найти
, для которого найти 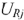 .
.
Возможно эти дополнительные страницы вам будут полезны:

