Оглавление:

| Здравствуйте! Я Людмила Анатольевна Фирмаль, занимаюсь помощью студентам более 17 лет. У меня своя команда грамотных, сильных преподавателей. Мы справимся с любой поставленной перед нами работой технического и гуманитарного плана. И неважно – она по объёму на две формулы или огромная, сложно структурированная, на 125 страниц! Нам по силам всё, поэтому не стесняйтесь, присылайте. |
| Если что-то непонятно — вы всегда можете написать мне в WhatsApp и я вам помогу! |
Как заказать выполнение заданий по линейной алгебре
Вы можете написать сообщение в WhatsApp. После этого я оценю ваш заказ и укажу стоимость и срок выполнения вашей работы. Если условия Вас устроят, Вы оплатите, и преподаватель, который ответственен за вашу работу, начнёт выполнение и в согласованный срок или, возможно, раньше срока Вы получите файл готовой работы в личные сообщения.
Сколько может стоить заказ
Стоимость заказа зависит от задания и требований Вашего учебного заведения. На цену влияют: сложность, количество заданий и срок выполнения. Поэтому для оценки стоимости заказа максимально качественно сфотографируйте или пришлите файл задания, при необходимости, загружайте поясняющие фотографии лекций, файлы методичек, указывайте свой вариант.
Какой срок выполнения заказа
Минимальный срок выполнения заказа составляет 2-4 дня, но помните, срочные задания оцениваются дороже.
Как оплатить заказ
Сначала пришлите задание, я оценю, после вышлю вам форму оплаты, в которой можно оплатить с баланса мобильного телефона, картой Visa и MasterCard, apple pay, google pay.
Гарантии и исправление ошибок
В течение 1 года с момента получения Вами готового решения заказа действует гарантия. В течении 1 года я и моя команда исправим любые ошибки в заказе.
Чуть ниже я предоставила теорию, она вам поможет освежить память и примеры оформления заказов по некоторым темам линейной алгебры, так я буду оформлять ваши работы если закажите у меня, это не все темы, это лишь маленькая часть их, чтобы вы понимали насколько подробно я оформляю.
Линейная алгебра. Матрицы
Рассмотрим систему уравнений 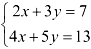
Составим таблицу, состоящую из чисел и заключим ее в круглые скобки:
а) Имеющую 2 строки (по числу уравнений, входящих в данную систему) и 2 столбца (по числу переменных): 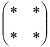 . Первую строку составим из коэффициентов первого уравнения, вторую — из коэффициентов второго. В первом столбце — коэффициенты перед переменной
. Первую строку составим из коэффициентов первого уравнения, вторую — из коэффициентов второго. В первом столбце — коэффициенты перед переменной 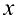 , во втором — коэффициенты перед переменной
, во втором — коэффициенты перед переменной 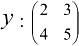
b) Имеющую 2 строки (по числу уравнений, входящих в данную систему) и 3 столбца (число переменных + 1 столбец свободных членов): 
Первую строку составим из коэффициентов первого уравнения, вторую — из коэффициентов второго. В первом столбце — коэффициенты перед переменной 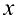 , во втором — коэффициенты перед переменной
, во втором — коэффициенты перед переменной  , в третьем — свободные члены:
, в третьем — свободные члены: 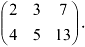
Эти таблицы называются
a) Матрицей
b) Расширенной матрицей данной системы уравнений.
Рассмотрим систему уравнений 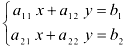 и составим для неё матрицу и расширенную матрицу системы:
и составим для неё матрицу и расширенную матрицу системы: 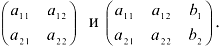
Рассмотрим ещё одну систему уравнений:
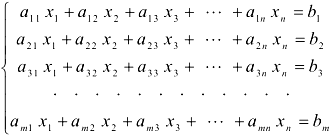
и составим для неё матрицу и расширенную матрицу системы.
Матрицей называется прямоугольная таблица чисел, содержащая 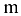 строк одинаковой длины (или
строк одинаковой длины (или 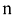 столбцов одинаковой длины). Строки и столбцы матрицы называются рядами матрицы.
столбцов одинаковой длины). Строки и столбцы матрицы называются рядами матрицы.
Матрицы обозначаются заглавными буквами латинского алфавита: 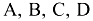 и т.д.
и т.д.
Матрица записывается в виде: 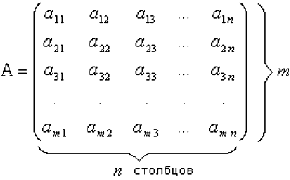
или сокращенно 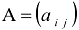 , где
, где 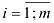 — номер строки, в которой расположен данный элемент;
— номер строки, в которой расположен данный элемент; 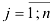 — номер столбца.
— номер столбца.
Если у матрицы 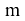 строк и
строк и 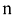 столбцов, то говорят, что её размерность
столбцов, то говорят, что её размерность 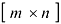 и пишут
и пишут 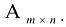
Матрица, у которой число строк равно числу столбцов, называется квадратной. Квадратную матрицу размерности 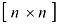 называют матрицей
называют матрицей 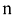 -го порядка.
-го порядка.
Числа 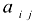 , у составляющие матрицу, называются её элементами.
, у составляющие матрицу, называются её элементами.
Элементы 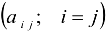 , расположенные на диагонали, идущей из левого верхнего угла в правый нижний — образуют главную диагональ матрицы. Элементы, расположенные на диагонали, идущей из правого верхнего угла в левый нижний образуют побочную диагональ матрицы.
, расположенные на диагонали, идущей из левого верхнего угла в правый нижний — образуют главную диагональ матрицы. Элементы, расположенные на диагонали, идущей из правого верхнего угла в левый нижний образуют побочную диагональ матрицы.
Квадратная матрица, у которой отличны от нуля только элементы главной диагонали, называется диагональной. 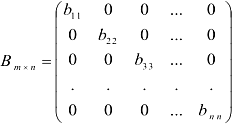
Диагональная матрица, у которой все элементы главной диагонали одинаковы, называется скалярной. 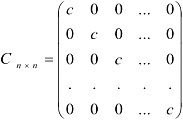
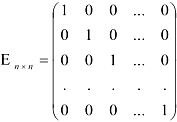
Скалярная матрица, у которой вес элементы главной диагонали равны 1, называется единичной.
Для неё есть специальное обозначение 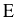 :
: 
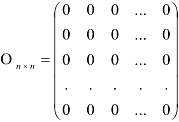
Матрица, все элементы которой равны нулю
называется нулевой и обозначается буквой 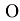 .
. 
Квадратная матрица называется треугольной, если все элементы,
расположенные по одну сторону от главной диагонали, равны нулю.
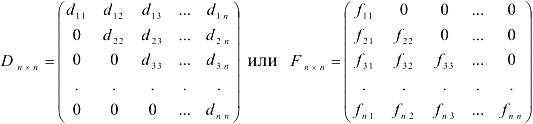
Матрица, состоящая только из одного столбца 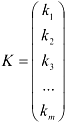 , называется вектор — столбцом.
, называется вектор — столбцом.
Матрица, состоящая только из одной строки 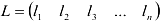
называется вектор — строкой.
Возможно эта страница вам будет полезна:
| Предмет линейная алгебра |
Действия над матрицами
- Матрицы называются равными, если равны вес соответствующие элементы этих матриц.
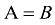 , если
, если 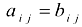 , где
, где 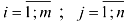 .
. - Сложение: (возможна только для матриц одинаковой размерности)
Суммой двух матриц называется матрица, каждый элемент которой является суммой соответствующих элементов исходных матриц.
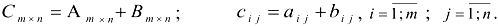
Пример:
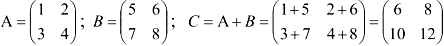
3. Разность: (возможна только для матриц одинаковой размерности) Разностью двух матриц называется матрица, каждый элемент которой является разностью соответствующих элементов исходных матриц.
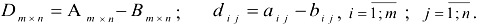
Пример:
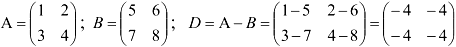
4. Умножение матрицы на число: Произведением матрицы на число называется матрица, каждый элемент которой равен произведению соответствующих элементов исходной матрицы на заданное число.
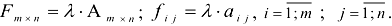
Пример:
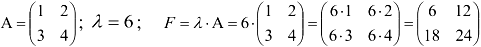
Матрица 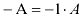 называется противоположной матрице
называется противоположной матрице 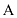 .
.
Операции сложения матриц и умножение матрицы на число обладают следующими свойствами:
a) 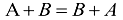 (переместительный закон)
(переместительный закон)
b) 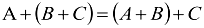 (сочетательный закон)
(сочетательный закон)
c) 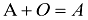
d) 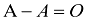
e) 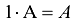
f) 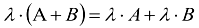
g) 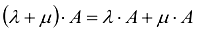
h) 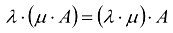
где 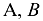 — матрицы,
— матрицы, 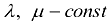 .
.
5. Произведение матриц: (возможно только если число столбцов первой матрицы равно числу строк второй матрицы).
Если даны 2 матрицы, размерность первой 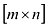 , а второй —
, а второй — 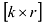 , то 1-ю матрицу можно умножить на вторую, если
, то 1-ю матрицу можно умножить на вторую, если 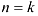 . Произведением будет матрица размерности
. Произведением будет матрица размерности 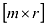 .
. 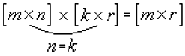
Нам даны 2 матрицы:
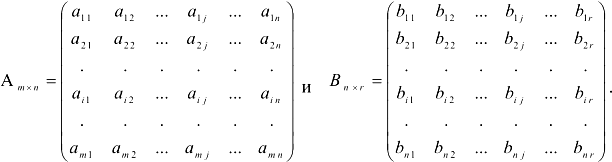
Произведением матрицы 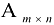 на матрицу
на матрицу 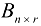 называется такая матрица у которой
называется такая матрица у которой 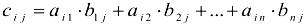 , где
, где 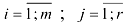 .
.
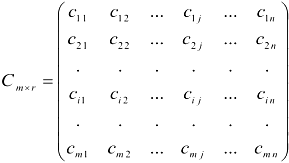
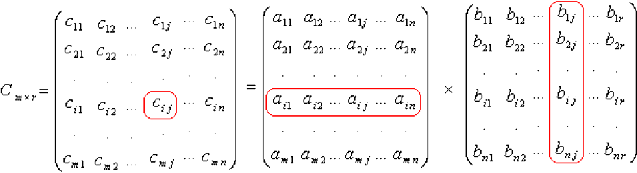
Т. е. элемент 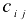 равен сумме произведений элементов
равен сумме произведений элементов 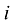 -й строки первой матрицы на соответствующие элементы
-й строки первой матрицы на соответствующие элементы 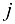 — го столбца второй матрицы.
— го столбца второй матрицы.
Рассмотрим умножение для матриц размерности 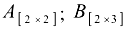 и
и 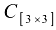 .
.
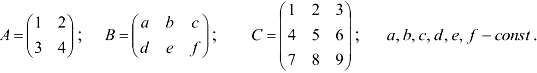
Можно найти произведения матриц: 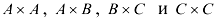 .
.
Найдем произведение матриц 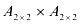 . Получим матрицу размерности
. Получим матрицу размерности 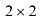 .
.
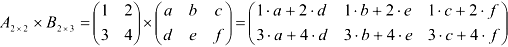
Найдем произведение матриц 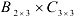 . Получим матрицу размерности
. Получим матрицу размерности 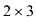 .
.
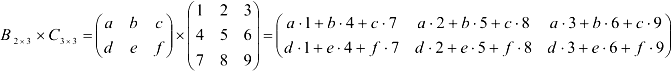
Найдем произведение матриц 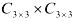 . Получим матрицу размерности
. Получим матрицу размерности 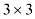 .
.
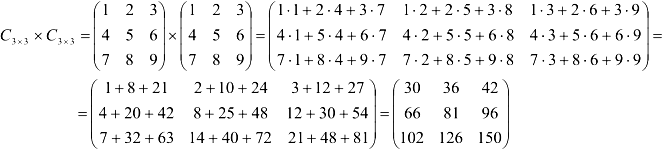
Найти произведения матриц 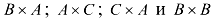 — нельзя.
— нельзя.
В общем случае (если оба произведения имеют смысл) 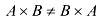 .
.
Если 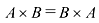 , то эти матрицы называются перестановочными.
, то эти матрицы называются перестановочными.
Произведение двух отличных от нуля матриц может быть равно нулевой матрице.
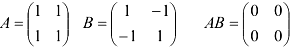
Операция умножения матриц обладает следующими свойствами:
a) 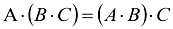 (сочетательный закон)
(сочетательный закон)
b) 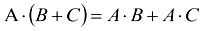 (распределительный закон)
(распределительный закон)
c) 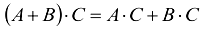
d) 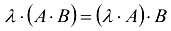
e) 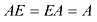
Матрица, у которой поменяли местами строки и столбцы, называется транспонированной к данной и обозначается
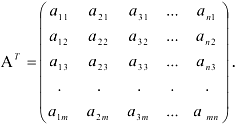
Например:
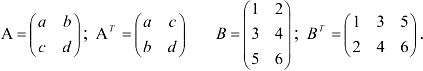
Транспонированная матрица обладает следующими свойствами:
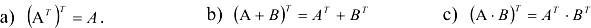
Возможно эта страница вам будет полезна:
| Решение задач по линейной алгебре |
Элементарные преобразования матриц
a. Перестановка местами двух строк (или двух столбцов) матрицы.
b. Умножение всех элементов строки (или всех элементов столбца) на число, отличное от нуля.
c. Прибавление ко всем элементам строки соответствующих элементов другой строки, умноженных на одно и то же число (или прибавление ко всем элементам столбца соответствующих элементов другого столбца, умноженных на одно и то же число).
Две матрицы называются эквивалентными, если одна из них получается из другой с помощью элементарных преобразований. 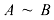 .
.
Матрица называется ступенчатой, если в каждой последующей строке первый отличный от нуля элемент расположен правее, чем в предыдущей. Матрицу можно привести к ступенчатому виду, используя элементарные преобразования.
Если все элементы строки матрицы равны нулю, то строка называется пулевой строкой.
Рангом матрицы будем называть число ненулевых строк матрицы ступенчатого вида.
Квадратной матрице n-го порядка можно поставить в соответствие число, называемое ее определителем (детерминантом): 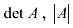 или
или  .
.
Определители вычисляется следующим образом:
- Определитель первого порядка:
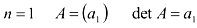
- Определитель второго порядка:
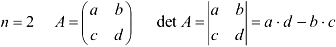
- Определитель третьего порядка:
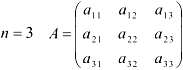
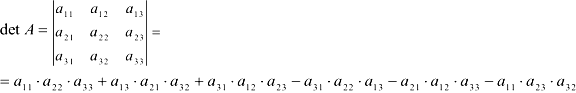
Правило Саррюса (правило треугольников):

или
 Перепишем ещё раз первую и вторую строчки определителя.
Перепишем ещё раз первую и вторую строчки определителя.
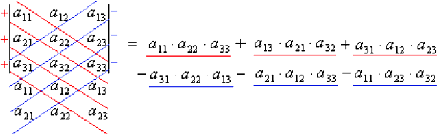
Проведём главную диагональ и две линии параллельные ей.
Затем проведём побочную диагональ и две параллельные ей линии.
Элементы, расположенные на линиях нужно перемножить.
Первые 3 произволения берутся со знаком  , последние — со знаком
, последние — со знаком  .
.
4. Определители высоких порядков вычисляются на основе определителей низших порядков.
В определителе 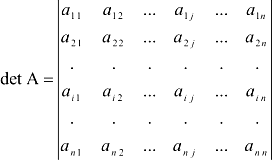 выберем элемент
выберем элемент 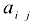 .
.
Вычеркнем строчку и столбец, на пересечении которых находится выбранный элемент.
Минором некоторого элемента 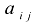 называется определитель, полученный вычеркиванием из исходного определителя столбца и строки, на пересечении которых находится данный элемент. Минор обозначается
называется определитель, полученный вычеркиванием из исходного определителя столбца и строки, на пересечении которых находится данный элемент. Минор обозначается 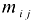 .
.
В определителе 3-го порядка
для элемента 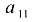 минор
минор 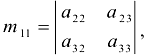
для элемента 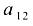 минор
минор 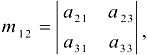
а для элемента 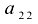 минор
минор 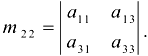
Алгебраическое дополнение элемента 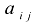 называется минор этого элемента, взятый со знаком » + «, если сумма
называется минор этого элемента, взятый со знаком » + «, если сумма 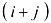 — четное число, и со знаком » — «, если
— четное число, и со знаком » — «, если 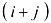 — нечетно.
— нечетно. 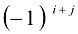 .
.
Алгебраическое дополнение обозначается 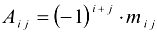 .
.
В определителе 3-го порядка
для элемента 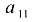 алгебраическое дополнение
алгебраическое дополнение 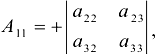
для элемента 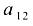 алгебраическое дополнение
алгебраическое дополнение 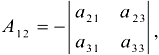
а для элемента 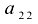 алгебраическое дополнение
алгебраическое дополнение 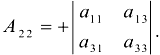
Свойства определителей
1) Определитель не изменится, если:
a. Его строки заменить столбцами и наоборот.
b. Если к элементам одной его строки прибавить соответствующие элементы другой его строки, умноженные на любое число.
2) При перестановке двух строк (или столбцов) определитель меняет знак.
3) Определитель равен нулю, если:
a. Определитель имеет нулевую строку (или нулевой столбец).
b. Определитель имеет 2 одинаковых строки (или 2 одинаковых столбца).
c. Все элементы строки (столбца) пропорциональны элементам другой строки (столбца).
4) Общий множитель элементов строки (или столбца) можно вынести за знак определителя.
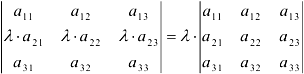
5) Если элементы строки (столбца) представляют собой сумму двух слагаемых, то определитель можно разложить на сумму двух соответствующих определителей: 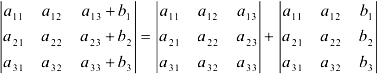
6) Определитель равен сумме произведений элементов строки (столбца) на соответствующие им алгебраические дополнения.
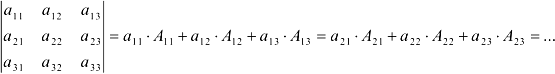
Используя это свойство, можно вычислять определители высших порядка.
7) Сумма произведений элементов строки (столбца) на алгебраические дополнения соответствующих элементов другой строки (столбца) равны нулю.
8) Определитель произведения матриц равен произведению их определителей.
Матрица называется невырожденной, если её определитель 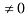 . Если
. Если 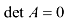 , то матрица называется вырожденной.
, то матрица называется вырожденной.
Из алгебраических дополнений оставим матрицу:
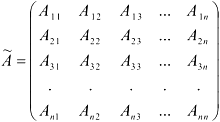
Союзной к матрице 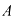 называется матрица
называется матрица 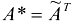 элементами которой являются алгебраические дополнения исходной матрицы.
элементами которой являются алгебраические дополнения исходной матрицы.
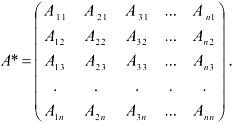
Матрица 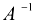 называется обратной к матрице
называется обратной к матрице 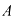 , если выполняется условие:
, если выполняется условие:
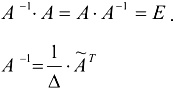
Всякая невырожденная матрица имеет обратную.
Найдем обратную матрицу к матрице
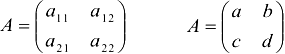
Вычислим 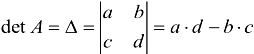 и убедимся, что он
и убедимся, что он 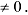
Найдем алгебраические дополнения для каждого элемента матрицы:
Алгебраическим дополнением элемента 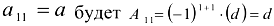
Алгебраическим дополнением элемента 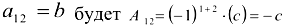
Алгебраическим дополнением элемента 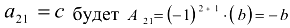
Алгебраическим дополнением элемента 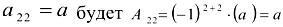
Из алгебраических дополнений оставим матрицу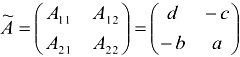
Транспонируем матрицу 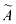 и получим союзную матрицу
и получим союзную матрицу
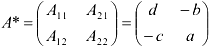
Найдем обратную матрицу 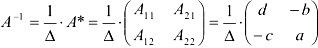
Сделаем проверку: 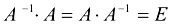
Аналогично вычисляется обратная матрица для 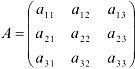
Вычислим 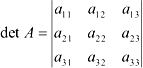 и убедимся, что он
и убедимся, что он 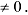
Найдем алгебраические дополнения для каждого элемента матрицы:
Алгебраическим дополнением элемента 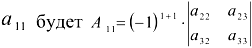
Алгебраическим дополнением элемента 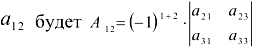
Алгебраическим дополнением элемента 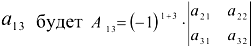
Алгебраическим дополнением элемента 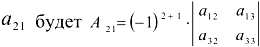
Алгебраическим дополнением элемента 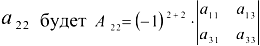
Алгебраическим дополнением элемента 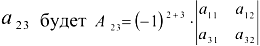
Алгебраическим дополнением элемента 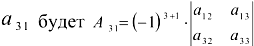
Алгебраическим дополнением элемента 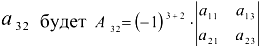
Алгебраическим дополнением элемента 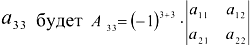
Из алгебраических дополнений оставим матрицу 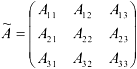
Транспонируем матрицу 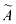 и получим союзную матрицу
и получим союзную матрицу 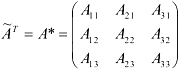
Найдем обратную матрицу 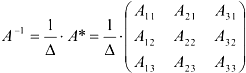
• Сделаем проверку: 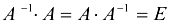 .
.
Например:
Найдем обратную матрицу к матрице 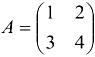
Вычислим 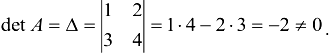
Найдем алгебраические дополнения для каждого элемента матрицы: Алгебраическим дополнением элемента 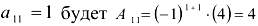
Алгебраическим дополнением элемента 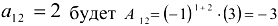
Алгебраическим дополнением элемента 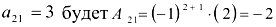
Алгебраическим дополнением элемента 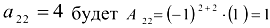
Из алгебраических дополнений оставим матрицу
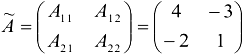
Транспонируем матрицу 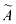 и получим союзную матрицу
и получим союзную матрицу
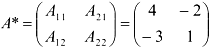
Найдем обратную матрицу 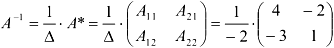
Сделаем проверку: 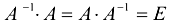
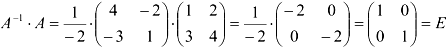
Вычислим обратную матрицу для 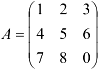
Вычислим 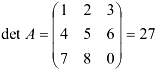 и убедимся, что он
и убедимся, что он 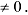
Найдем алгебраические дополнения для каждого элемента матрицы:
Для элемента 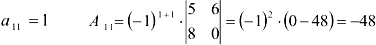
Для 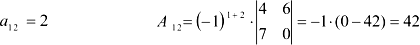
Для 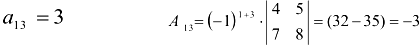
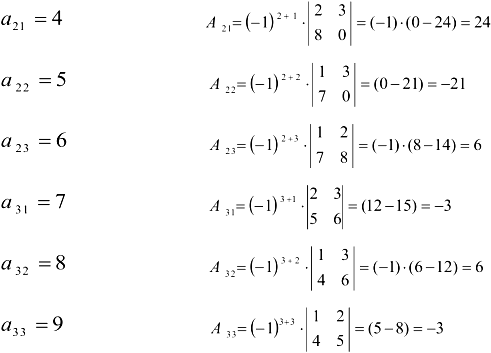
Из алгебраических дополнений оставим матрицу
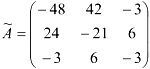
Транспонируем матрицу 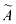 и получим союзную матрицу
и получим союзную матрицу
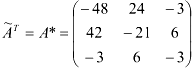
Найдем обратную матрицу
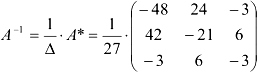
Сделаем проверку: 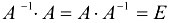
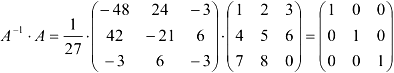
Решение систем линейных уравнений Методом Крамера.
Формулы Крамера: 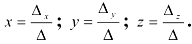
Возможно эта страница вам будет полезна:
| Помощь с линейной алгеброй |
Примеры оформления заказов по линейной алгебре
Пример оформления заказа №1:
Нам дана система уравнений 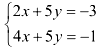
- Вычислим главный определитель системы и убедимся, что он
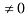 (если
(если 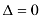 , решаем систему методом Гаусса.)
, решаем систему методом Гаусса.)
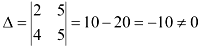
2. Вычислим 2 дополнительных определителя, которые получаются из главного определителя системы заменой одного из столбцов на вектор-столбец свободных членов.
При вычислении определителя 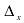 на вектор-столбец свободных членов заменим столбец, составленный из коэффициентов перед переменной
на вектор-столбец свободных членов заменим столбец, составленный из коэффициентов перед переменной 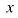 :
:
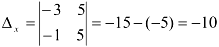
При вычислении определителя 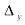 на вектор-столбец свободных членов заменим столбец, составленный из коэффициентов перед переменной
на вектор-столбец свободных членов заменим столбец, составленный из коэффициентов перед переменной 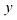 :
:
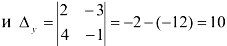
3. Вычислим 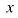 и
и 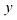 по формулам Крамера:
по формулам Крамера: 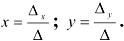
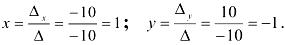 Получили решение системы:
Получили решение системы: 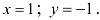
Сделаем проверку: подставим решения системы в каждое их уравнений.
Если мы решили верно, то каждое уравнение превратится в тождество.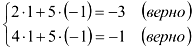
Если хоть одно из уравнений в тождество не превратится, значит система решена не верно.
Возможно эта страница вам будет полезна:
| Заказать контрольную работу по линейной алгебре |
Пример оформления заказа №2:
Нам дана система уравнений 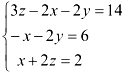 Перепишем систему уравнений так, чтобы в первом столбце стояла переменная
Перепишем систему уравнений так, чтобы в первом столбце стояла переменная 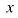 , во втором —
, во втором — 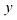 , в третьем — z :
, в третьем — z : 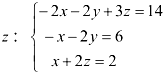
- Вычислим главный определитель системы (составленный из коэффициентов перед переменными) и убедимся, что он
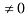 (если
(если 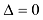 , решаем систему методом Гаусса.)
, решаем систему методом Гаусса.)
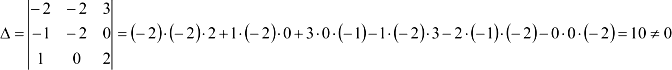
2. Вычислим 3 дополнительных определителя, которые получаются из главного определителя системы заменой одного из столбцов главного определителя на вектор-столбец свободных членов 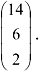
При вычислении определителя 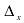 на вектор-столбец свободных членов заменим столбец
на вектор-столбец свободных членов заменим столбец 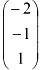 , составленный из коэффициентов, стоящих перед переменной
, составленный из коэффициентов, стоящих перед переменной 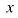 .
.
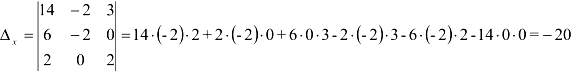
При вычислении определителя 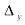 на вектор-столбец свободных членов заменим столбец
на вектор-столбец свободных членов заменим столбец 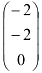 , составленный из коэффициентов, стоящих перед переменной
, составленный из коэффициентов, стоящих перед переменной 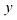 :
:
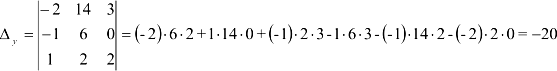
3. Вычислим 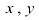 и
и 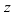 по формулам Крамера:
по формулам Крамера: 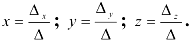
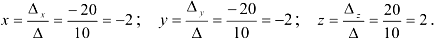
Получили решение системы: 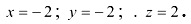
4. Сделаем проверку: подставим решения системы в каждое их уравнений.
Если мы решили верно, то каждое уравнение превратится в тождество.
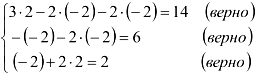
Решение систем линейных уравнений матричным методом.
Возможно эта страница вам будет полезна:
| Готовые контрольные работы по линейной алгебре |
Пример оформления заказа №3:
Нам дана система уравнений 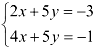
Систему линейных уравнений можно представить в матричном виде: 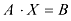 , где
, где 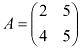 — матрица системы,
— матрица системы, 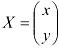 — вектор-столбец неизвестных,
— вектор-столбец неизвестных, 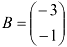 — вектор-столбец свободных членов.
— вектор-столбец свободных членов.
(Проверим. Умножим матрицу 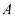 на
на 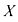 и приравняем к
и приравняем к 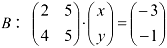
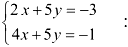 мы получили исходную систему.)
мы получили исходную систему.)
Для того, чтобы найти неизвестные 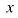 и
и 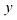 в уравнении
в уравнении 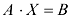 , нужно избавиться от множителя
, нужно избавиться от множителя 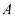 . Для этого нужно умножить слева на обратную матрицу обе части уравнения:
. Для этого нужно умножить слева на обратную матрицу обе части уравнения: 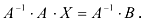
Т.к. 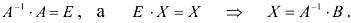
I. Вычислим главный определитель системы и убедимся, что он 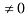 (если
(если 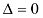 , решаем систему методом Гаусса.)
, решаем систему методом Гаусса.) 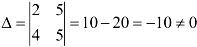
2. Найдем обратную матрицу 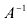

Из алгебраических дополнений оставим матрицу
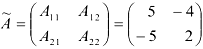
Транспонируем матрицу 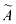 и получим союзную матрицу
и получим союзную матрицу
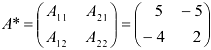
Найдем обратную матрицу 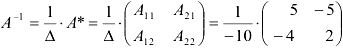
Сделаем проверку: 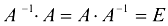
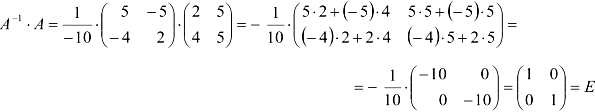
Итак 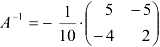
3. Умножим слева на 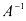 обе части уравнения:
обе части уравнения:
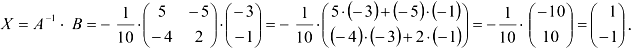
В первой строке находится значение неизвестной л, а во второй — значение неизвестной 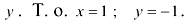
4. Сделаем проверку решения: 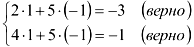
Пример оформления заказа №4:
Нам дана система уравнений 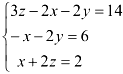
Перепишем систему уравнений так, чтобы в первом столбце стояла неизвестная 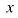 , во втором —
, во втором — 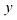 , в третьем —
, в третьем — 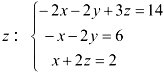
- Вычислим главный определитель системы (составленный из коэффициентов перед неизвестными) и убедимся, что он
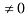
(если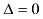 , решаем систему методом Гаусса.)
, решаем систему методом Гаусса.)
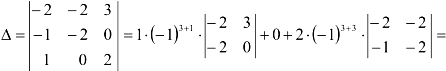
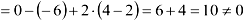
2. Найдем обратную матрицу.

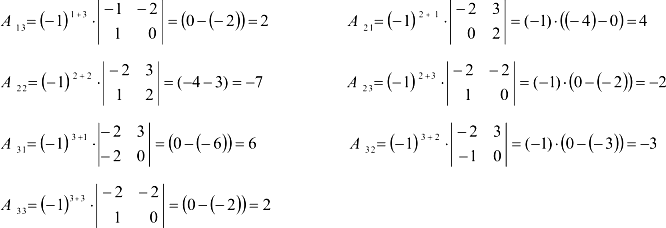
Из алгебраических дополнений оставим матрицу 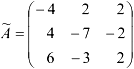
Транспонируем матрицу 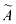 и получим союзную матрицу
и получим союзную матрицу 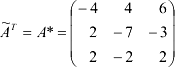
Найдем обратную матрицу 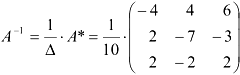
Сделаем проверку: 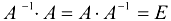
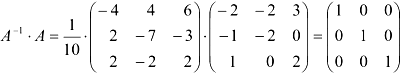
3. Умножим вектор-столбец свободных членов слева на 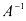 :
:
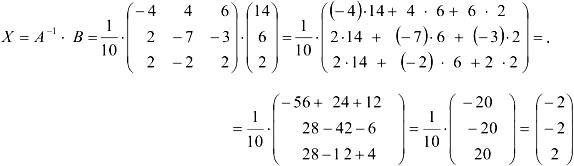
В первой строке находится значение неизвестной 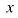 , во второй — значение неизвестной
, во второй — значение неизвестной 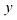 , а в третьей — значение
, а в третьей — значение 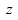 . Т. о.
. Т. о. 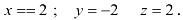
4. Сделаем проверку решения: 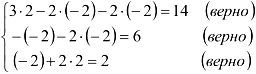
Пример оформления заказа №5:
Решить систему линейных алгебраических уравнений матричным способом:
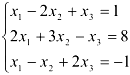
Выпишем матрицу коэффициентов при неизвестных 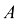 ; — матрицу-столбец неизвестных
; — матрицу-столбец неизвестных 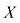 и матрицу-столбец свободных членов
и матрицу-столбец свободных членов 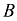 :
:
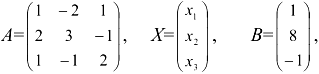
I. Проверим, будет ли матрица 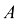 невырожденной (вычислим ее определитель
невырожденной (вычислим ее определитель  и убедимся, что он отличен от нуля).
и убедимся, что он отличен от нуля).
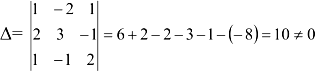
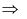 матрица
матрица 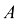 невырожденная и имеет обратную матрицу
невырожденная и имеет обратную матрицу 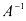 .
.
2. Вычислим алгебраические дополнения 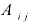 элементов определителя матрицы
элементов определителя матрицы 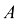 .
.
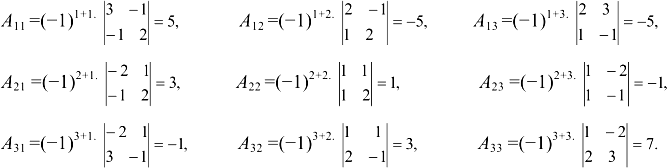
Тогда 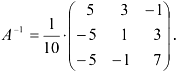
3. Умножим вектор-столбец свободных членов слева на 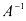 :
:
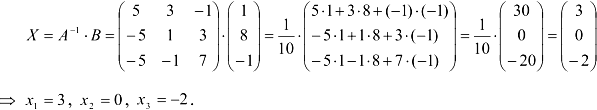
4. Сделаем проверку решения: