Заказать экономико математические методы ЭММ — решение на заказ онлайн

Здравствуйте! Я Людмила Анатольевна Фирмаль, занимаюсь помощью студентам более 17 лет. У меня своя команда грамотных, сильных преподавателей. Мы справимся с любой поставленной перед нами работой технического и гуманитарного плана. И неважно – она по объёму на две формулы или огромная, сложно структурированная, на 125 страниц! Нам по силам всё, поэтому не стесняйтесь, присылайте.

Если что-то непонятно — вы всегда можете написать мне в WhatsApp и я вам помогу!

Как заказать выполнение заданий по экономико математическим методам

Вы можете написать сообщение в WhatsApp. После этого я оценю ваш заказ и укажу стоимость и срок выполнения вашей работы. Если условия Вас устроят, Вы оплатите, и преподаватель, который ответственен за вашу работу, начнёт выполнение и в согласованный срок или, возможно, раньше срока Вы получите файл готовой работы в личные сообщения.

Сколько может стоить заказ экономико математических методов

Стоимость заказа зависит от задания и требований Вашего учебного заведения. На цену влияют: сложность, количество заданий и срок выполнения. Поэтому для оценки стоимости заказа максимально качественно сфотографируйте или пришлите файл задания, при необходимости, загружайте поясняющие фотографии лекций, файлы методичек, указывайте свой вариант.

Какой срок выполнения заказа

Минимальный срок выполнения заказа составляет 2-4 дня, но помните, срочные задания оцениваются дороже.

Как оплатить заказ

Сначала пришлите задание, я оценю, после вышлю вам форму оплаты, в которой можно оплатить с баланса мобильного телефона, картой Visa и MasterCard, apple pay, google pay.

Гарантии и исправление ошибок

В течение 1 года с момента получения Вами готового решения заказа действует гарантия. В течении 1 года я и моя команда исправим любые ошибки в заказе.

Чуть ниже я предоставила примеры оформления заказов по некоторым темам предмета экономико математические методы, так я буду оформлять ваши работы если закажите у меня, это не все темы, это лишь маленькая часть их, чтобы вы понимали насколько подробно я оформляю.

Возможно эта страница вам будет полезна:

Предмет экономико-математические методы (ЭММ)

Пример оформления заказа на тему: решения задачи линейной оптимизации

Типовая задача. Предприятие может выпускать четыре вида продукции 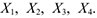Для их изготовления используются три вида ресурсов 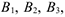объемы которых ограничены. Известна прибыль, получаемая от реализации единицы продукции каждого вида продукции: 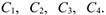Известны потребности в ресурсах для выпуска единицы каждого вида продукции. Заданы ограничения, накладываемые на объемы выпускаемой продукции. Требуется определить оптимальное количество выпуска каждого вида продукции, при котором будет получена максимальная прибыль.

Рассмотрим конкретную задачу, математическая модель которой имеет следующий вид [Матвеев, с.268].

Решение задачи оптимизации:

• Создадим модель задачи в виде таблицы Excel:

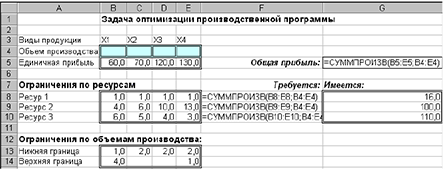
• Выбор вкладки «Сервис + Поиск решения

• Установим целевую ячейку: G5
• Укажем изменяемые ячейки: В4: Е4
• Введем ограничения воспользуясь функцией

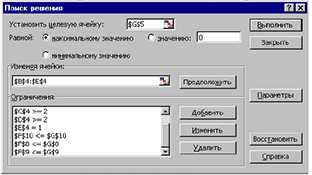
• Введем параметры для решения задачи с помощью функции «Параметры».
• Установим флажок «Линейная модель»;
• Установим флажок «Неотрицательные значения»;
• «OK».
• Выполним задачу оптимизации с помощью функции «Выполнить». Результаты приведены в следующей таблице.

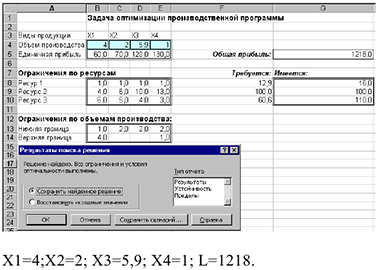
Создание отчетов по результатам заказа с решением задачи и её анализа:

Необходимо выбрать все три типа отчета и нажать на «ОК.». Будут сформированы три листа с отчетами, которые можно просматривать по выбору.

• Отчет по результатам.

В режиме «Результаты поиска решения»» выберем тип отчета «Результаты».В отчет включаются исходные и конечные значения целевой функции и изменяемых переменных, дополнительные сведения об ограничениях. По ограничениям (ресурсам) указывается их дефицитность (связанность), а если ресурс является недифицитным, то указывается избыток.

• Отчет по устойчивости.

Отчет содержит сведения о чувствительности решения к малым отклонениям изменяемых ячеек (искомых переменных, т.е. объемов производства) или в формулах ограничений (величин ресурсов), а также коэффициентов целевой функции (величин единичной прибыли).

По каждой переменной указывается:

• результирующее (оптимальное) значение (объема производства);
• редуцированная (нормированная) стоимость единицы продукта;
• допустимое увеличение объема производства;
• допустимое уменьшение объема производства.

Редуцированная стоимость 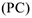данной продукции 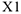равна:

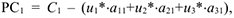
где 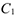— единичная прибыль; 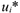— теневая (реальная) цена 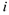-го ресурса; 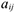— ресурс 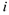— го вида, необходимый для производства единицы 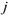— го продукта. Правая часть данного выражения характеризует реальную стоимость единицы продукта по теневым ценам ресурсов. Тогда можно рассматривать как реальную эффективность производства единицы продукции по теневым ценам.

При заданных величинах 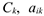для нового (либо для выпускаемого) продукта можно оценить эффективность его производства. При < 0 производство данного продукта неэффективно (для задачи поиска максимума целевой функции).

По каждому ограничению отчет по устойчивости содержит:

• результирующее значение (заданный объем ресурса);
• теневая цена (нормированная или реальная стоимость, учитывающая дефицитность) ресурса;
• фактический уровень использования (расход) ресурса на план производства;
• допустимое увеличение объема ресурса;
• допустимое уменьшение объема ресурса.

Теневая цена ограничения выражает размер изменения целевой функции при увеличении объема только данного ресурса на единицу. Она может быть положительной, нулевой и отрицательной.

По каждому коэффициенту целевой функции указываются:

• заданное значение;
• допустимое увеличение;
• допустимое уменьшение.

Допустимое изменение одного показателя целевой функции не приводит к изменению найденного решения.

Одновременное изменение нескольких показателей целевой функции также не приводит к изменению найденного решения, если они имеют ненулевые значения редуцированной стоимости. При наличии нулевых значений редуцированной стоимости доли изменений нескольких коэффициентов в допустимом интервале (в одном направлении) в сумме должны быть не более 1.

• Отчет по пределам. Содержит оптимальные значения целевой функции (прибыли) и независимых переменных (объемов производства), а также значение целевой функции для предельных значений независимых переменных при сохранении других переменных и ограничений без изменений.

Пример оформления заказа на тему: решения задачи оптимизации плана производства в рыночных условиях

Цель: решить и проанализировать задачу оптимизации плана производства в рыночных условиях.

Задачи:

1. Рассмотреть постановку задачи оптимизации плана производства в рыночных условиях.
2. Построить математическую модель задачи оптимизации плана производства в рыночных условиях.
3. Произвести по исходным данным решение задачи оптимизации в Excel, проанализировать решение.

Рассмотрим динамическую однопродуктовую модель оптимизации плана производства.

Постановка задачи:

Предприятие производит продукцию одного вида, для которой требуется один вид сырья. На каждый месяц известны значения ожидаемого спроса 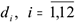и номинальные производственные мощности 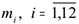(под производственной мощностью понимается максимальный объем продукции, который можно произвести за месяц). Известен технологический коэффициент 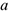, показывающий объем необходимого сырья на единицу готовой продукции. Известен начальный запас готовой продукции 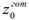на начало планового периода. На каждый месяц известна оптовая цена 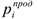продажи единицы продукции; стоимость 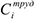труда, затраченного рабочим коллективом на производство единицы продукции; стоимость 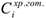хранения единицы готовой продукции на складе; переменные производственные затраты 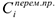на единицу продукции.

Требуется найти оптимальные объемы выпуска продукции 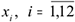и запасы готовой продукции 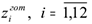по месяцам

Построение модели

Для решения задачи построим модель в виде задачи математического программирования. Для такого рода задач, как уже известно, необходимо определить целевую функцию и ограничения. В качестве целевой функции выберем разницу 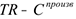получаемого от продажи дохода и общих затрат на производство продукции без учета издержек на материально-техническое обеспечение. В состав общих переменных затрат 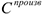на производство продукции входят: переменные производственные затраты 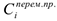; суммарная стоимость труда 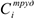, затраченного рабочим коллективом на производство единицы продукции; суммарные затраты 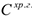на хранение готовой продукции на складе. Определим составляющие целевого функционала

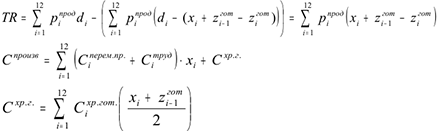
В качестве ограничений для модели выберем ограничения по производственной мощности 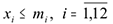и ограничения, накладываемые на объемы запасов готовой продукции

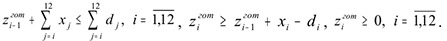
Подставив выражения в целевую функцию, получим математическую модель в виде:

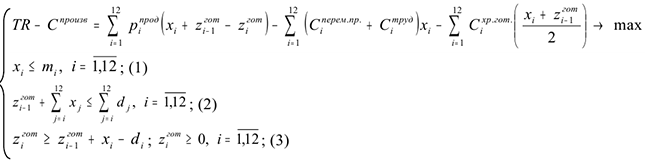
Ограничение (1) показывает, что необходимо производить продукцию в объемах, не превышающих доступные производственные мощности. Ограничение (2) показывает, что необходимо создавать запасы готовой продукции с целью удовлетворения высокого спроса в будущем. Ограничения (3) задают характер изменения запасов готовой продукции.

Решение:

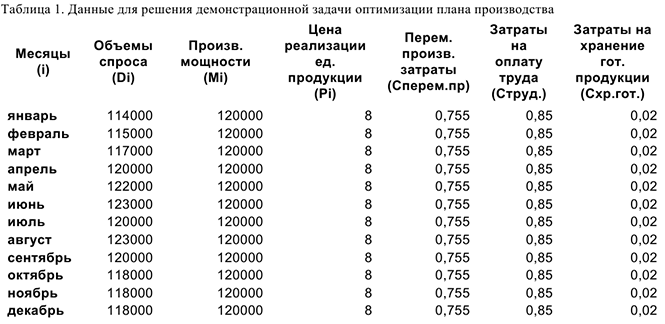
Решим задачу при следующих данных

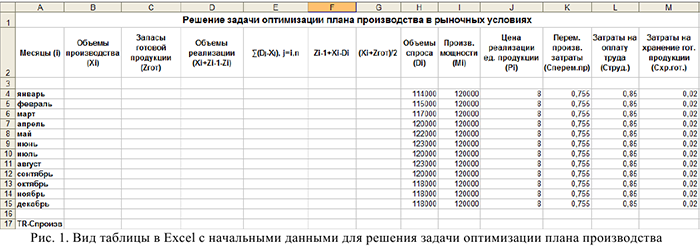
2) Провести вспомогательные вычисления. Для этого необходимо заполнить формулами столбцы как на рис. 2,3,4,5. После ввода формулы ловим «черный крест» в правом нижнем углу и растягиваем ячейку на все месяцы, таким образом, столбец заполнится формулами.

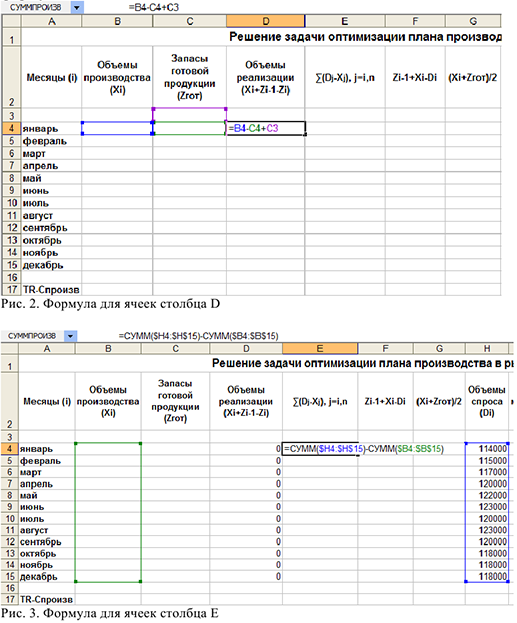
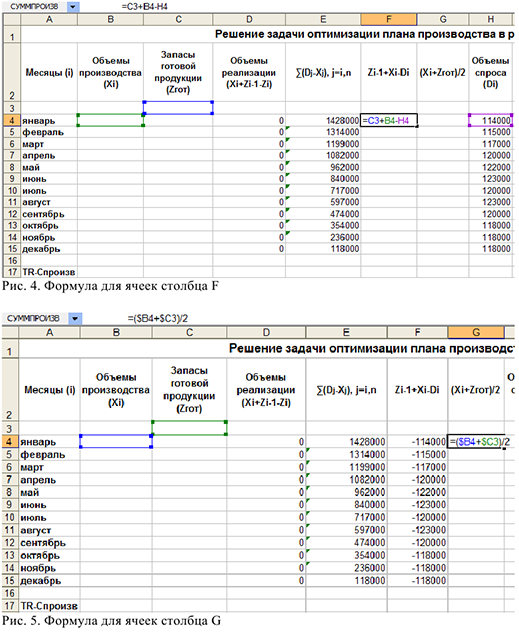
3) Ввести соответствующую математической модели формулу для разницы 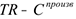ячейку В17 (см. рис. 6.)

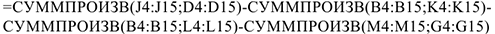
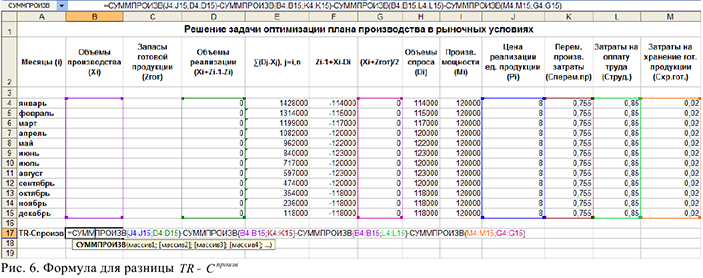
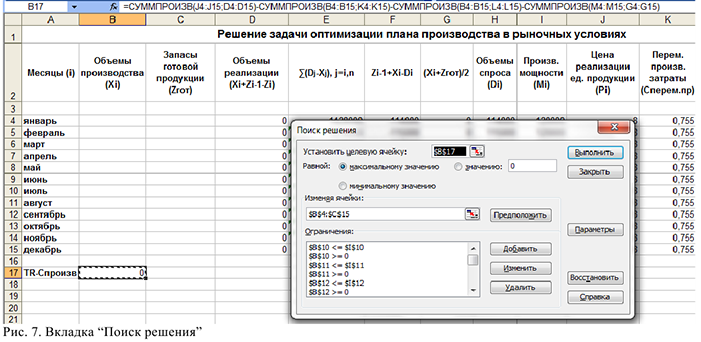
4) Запустить «Поиск решения»: установить целевую ячейку В17; выбрать оптимизацию по максимальному значению; выбрать изменяемые ячейки В4:С15, которые нам нужно найти в результате решения; ввести ограничения, исходя из математической модели. Также на вкладке «Параметры» нужно выбрать параметры «Линейная модель», «Неотрицательные значения». После того как все заполнено нажать кнопку «Выполнить», (см. рис. 7)

После вычислений получим следующие данные объемов производства и запасов готовой продукции помесячно (см. рис .8.)

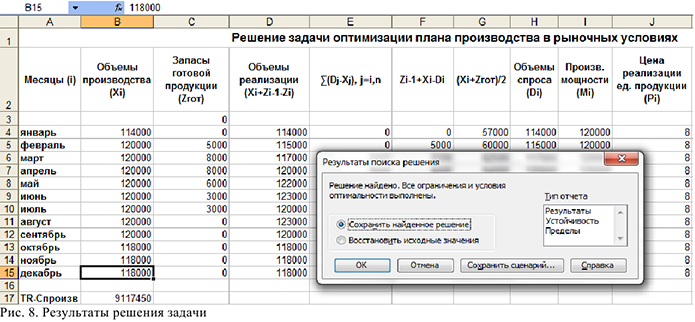
Результаты модели показывают, в каких объемах необходимо производить продукцию, чтобы получить максимальный доход, а также величину этого дохода и объемы оставшихся на конец месяца запасах готовой продукции на складе.

По полученным результатам средствами Excel возможно построить диаграмму, чтобы сравнить, например спрос и полученные объемы производства (предложение). Для этого необходимо выбрать столбцы с данными об объемах производства и спроса. Затем при помощи мастера диаграмм построить график.

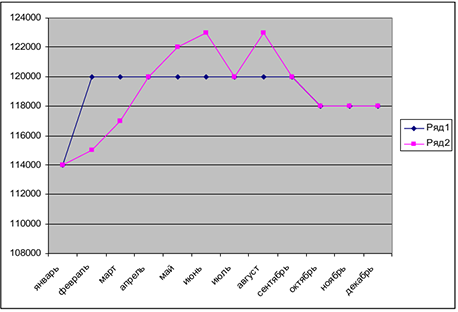
Пример оформления заказа на тему: решения задачи оптимизации плана закупок

Цель: решить и проанализировать задачу оптимизации плана закупок на основе данных производства.

Задачи:

1. Рассмотреть существующие модели управления запасами.
2. Рассмотреть постановку задачи оптимизации плана закупок.
3. Построить математические модели задачи оптимизации плана закупок с использованием существующих моделей управления запасами.
4. Произвести по исходным данным решение задачи оптимизации в Excel, проанализировать решение.

Существуют две основные стратегии (модели) управления запасами:

1. Модель с фиксированным размером заказа — при этой модели заказы на поставку сырья осуществляются в момент снижения запаса сырья на складе до заранее определенного (порогового) уровня на фиксированную величину .
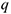2. Модель с фиксированным интервалом между заказами — при этой модели, как ясно из названия, заказы делаются в строго определенные моменты времени, которые отстоят друг от друга на равные интервалы, например 1 раз в месяц, 1 раз в неделю и т.п. Пополнение запаса происходит на величину необходимую для производства продукции до следующего пополнения.

Произведем оптимизацию плана закупок при помощи моделей движения сырья, используя при этом модели управления запасами.

Постановка задачи

Предприятие производит продукцию одного вида, для которой требуется один вид сырья. На каждый месяц известны объемы производства 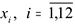продукции. Известен технологический коэффициент 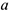, показывающий объем необходимого сырья на единицу готовой продукции и начальный запас сырья 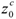на начало планового периода. На каждый месяц известна цена 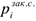закупки сырья и цена 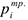транспортировки и отгрузки единицы сырья. Известна стоимость 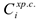хранения единицы сырья на складе и затраты 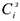на выполнение одного заказа поставки сырья. При управлении запасами сырья используется одна из двух основных моделей (модель с фиксированным размером заказа, модель с фиксированным интервалом времени между заказами).

Требуется найти оптимальные объемы выпуска продукции 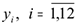и запасы сырья 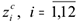по месяцам.

Построение модели

Для решения задачи построим модель в виде задачи математического программирования. Для такого рода задач, как уже известно, необходимо определить целевую функцию и ограничения. В качестве целевой функции выберем материальные затраты 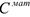, которые необходимо минимизировать. В состав материальных затрат входят затраты на закупку 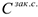, пополнение 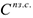, хранение сырья 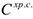, т.е. 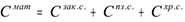(1), где

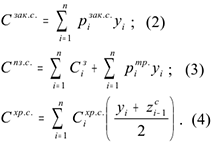
При вычислении затрат на пополнение запаса учитывались расходы на транспортировку сырья до места производства, которые в общем случае прямо пропорциональны объемам закупок.

В качестве ограничений выберем ограничения, обеспечивающие пополнение запасов до уровня не менее чем требуется для производства продукции.

При использовании модели с фиксированным интервалом между заказами получаем модель в виде задачи линейной оптимизации:

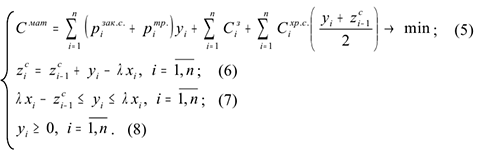
При использовании модели с фиксированным размером заказа, закупки производятся партиями 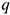. Для построения модели введем числа 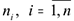, показывающие количество закупок объемом , необходимых на 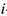-ый месяц. Тогда объем закупки на 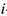-ый месяц будет определяться выражением 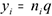. С учетом предположений, определим составляющие целевой функции материальных затрат:

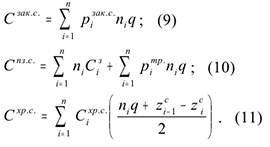
После подстановки выражений (9) — (11) в целевую функцию, получаем модель вида:

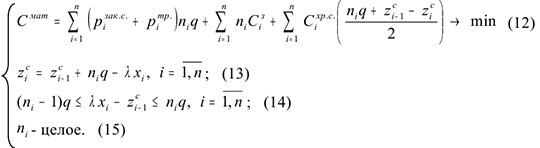
Решение задачи:

Решим задачу при следующих данных

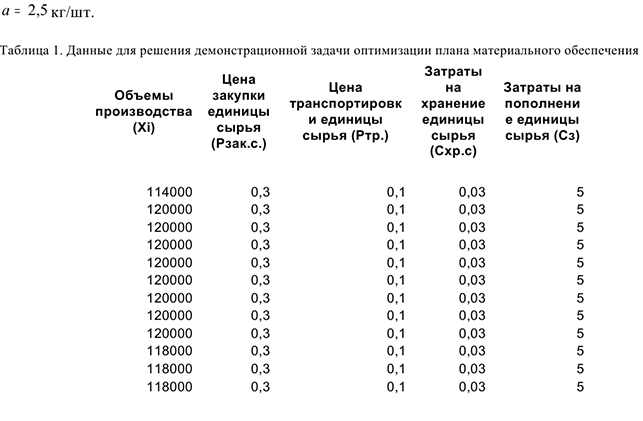
Решим задачу в Excel при помощи надстройки «Поиск решения», используя модель с фиксированным интервалом времени между заказами. Для этого необходимо:

1) Заполнить таблицу данными об объемах производства, ценах и затратах как показано на рис. 1.

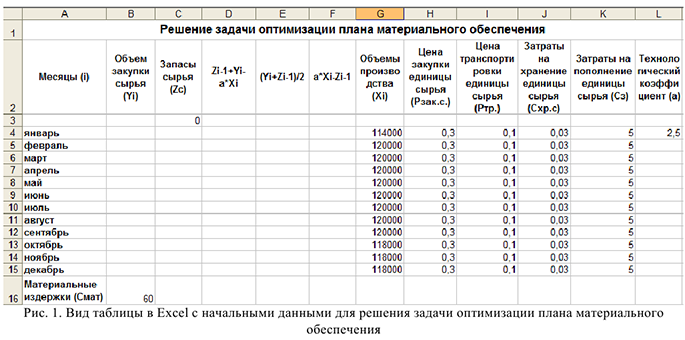
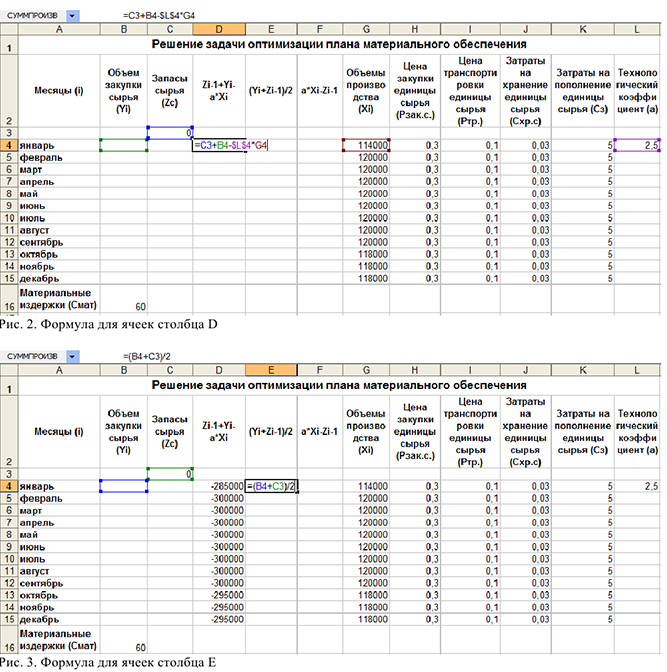
2) Провести вспомогательные вычисления. Для этого необходимо заполнить формулами столбцы как на рис. 2,3,4. После ввода формулы ловим «черный крест» в правом нижнем углу и растягиваем ячейку на все месяцы, таким образом, столбец заполнится формулами.

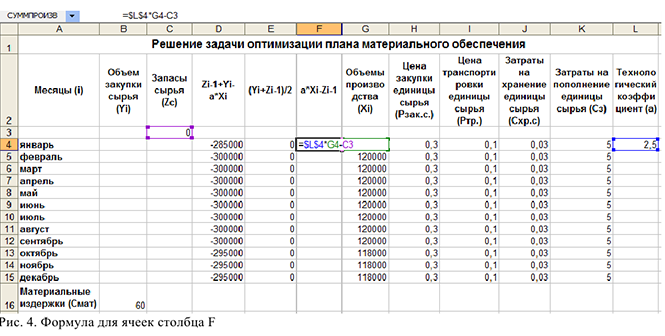
3) Ввести соответствующую математической модели формулу для материальных затрат 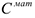в ячейку В16 (см. рис. 5.)

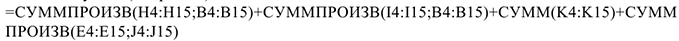
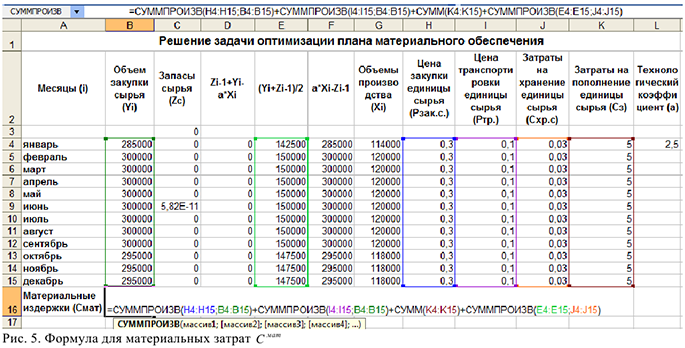
4) Запустить «Поиск решения»: установить целевую ячейку В16; выбрать оптимизацию по максимальному значению; выбрать изменяемые ячейки В4:С15, которые нам нужно найти в результате решения; ввести ограничения, исходя из математической модели. Также на вкладке «Параметры» нужно выбрать параметры «Линейная модель», «Неотрицательные значения». После того как все заполнено нажать кнопку «Выполнить», (см. рис. 6)

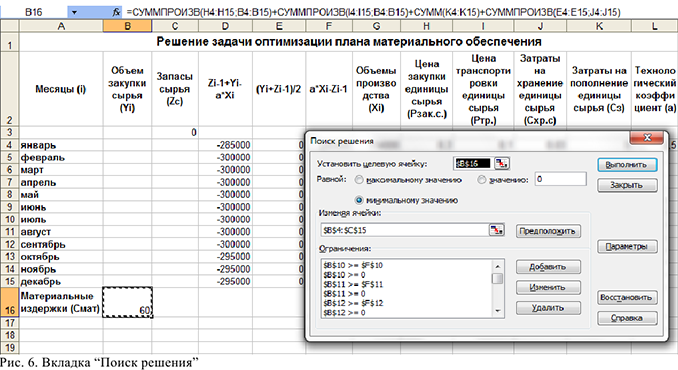
После вычислений получим следующие данные объемов закупки сырья и запасов сырья на каждый месяц (см. рис .7)

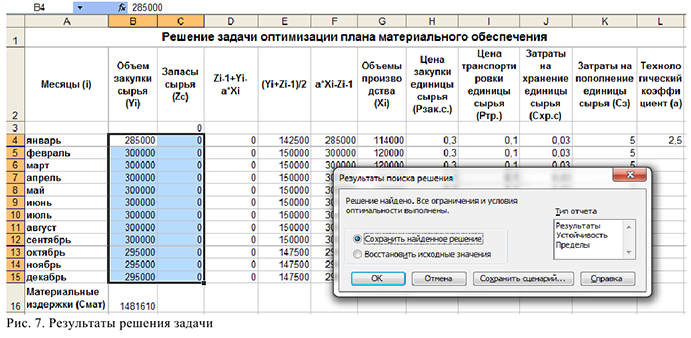
Результаты модели показывают, в каких объемах необходимо осуществлять закупки сырья у поставщика, а также объемы оставшихся на конец месяца запасах сырья на складе.

Возможно эти страницы вам будут полезны:

• Экономико-математические методы задачи с решением и примерами
• Решение задач по ЭММ
• Решение экономико математических методов
• Помощь по экономико математическим методам
• Курсовая работа по экономико математическим методам
• Контрольная по экономико математическим методам