Задачи, содержащие «скрытый» модуль

Задачи, содержащие «скрытый» модуль

В некоторых задачах модуль присутствует неявно, принимая форму, например, квадратного корня из квадрата некоторого выражения. Если при этом извлечь этот корень, руководствуясь правилом 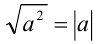, то в задаче появляется модуль.

Выбранный способ решения задачи также может подразумевать переход к модулю. Например, простейшие квадратные уравнения и неравенства, приведённые ниже, достаточно легко решаются извлечением корня (переходом к модулю):

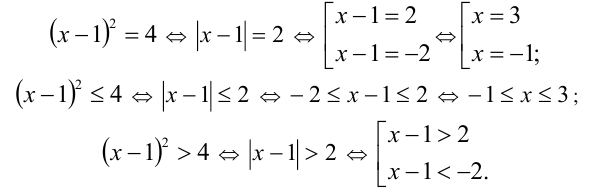
Пример №280.

Решить неравенство

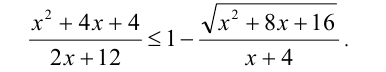
Решение:

Так как 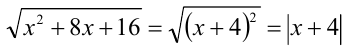то неравенство можно переписать в виде:

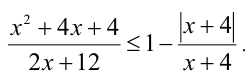
1) Если 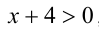, то неравенство принимает вид 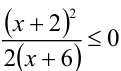Будем упрощать дальше. Поскольку в рассматриваемом случае 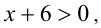то получаем неравенство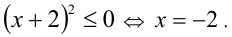

2) Если 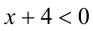, то неравенство принимает вид

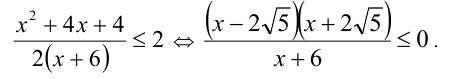
Поскольку в данном случае 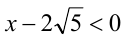, то имеем

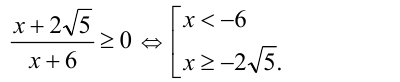
Осталось учесть 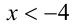Ответ: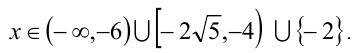

Пример №281.

Решить уравнение

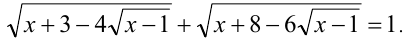
Решение:

Сделаем замену переменной, положив 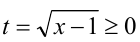. Отсюда находим 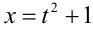, и, подставляя в уравнение, получим:

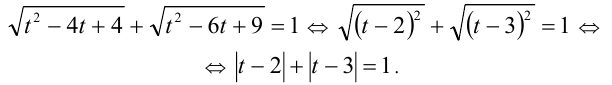
Решая последнее уравнение методом интервалов, найдём

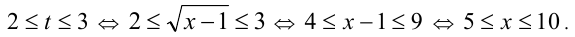
Пример №282.

Изобразить на координатной плоскости (х;y) множество точек, координаты которых удовлетворяют

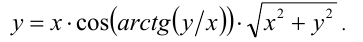
Решение:

ОДЗ: 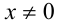. Так как 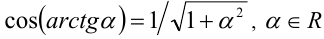, то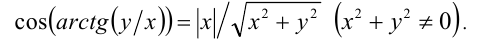

Подставляя в уравнение и упрощая, получаем 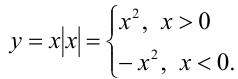Осталось на ОДЗ построить график (сделайте это самостоятельно).

Пример №283.

Ниже в примере 3 пункта 2.3 будет показано, как свести уравнение вида 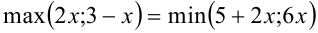к равносиль-ному ему уравнению с модулями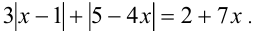

Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:

Предмет математика

Эти страницы возможно вам будут полезны:

Умножение на сопряжённое выражение в математике с примером решения

Замена в неравенствах множителей множителями эквивалентного знака

Использование свойств модулей для решения задач с примерами решения

Схемы решения типовых задач с применением модуля