Оглавление:
Свойства сумм Дарбу
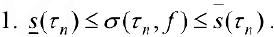
2. Если измельчить разбиение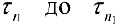 
добавляя новые точки, то 
.
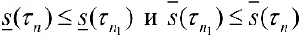3. Если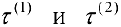 
— два произвольных разбиения отрезка 
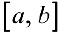, то 
.
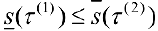4. Для того, чтобы ограниченная па отрезке 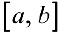функция 
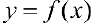была интегрируема, необходимо и достаточно, чтобы
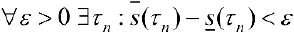
и при выполнении (6):
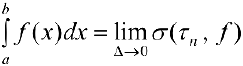, где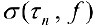 
— любая последовательность интегральных сумм, у которой 
.
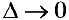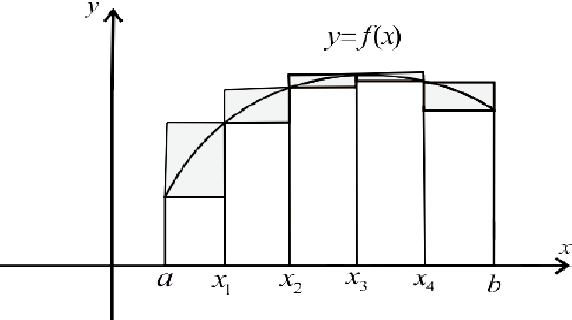
Рис.5.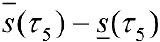 
.
Задача №50
Доказать, что функция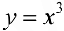 
интегрируема на отрезке [2, 3] и найти 
.
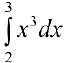Решение:
Разобьем отрезок [2, 3] на п равных отрезков точками:
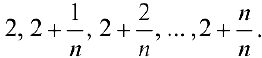
Тогда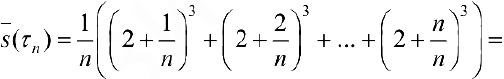 
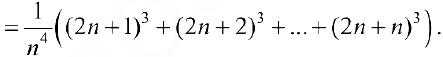
Воспользуемся формулой: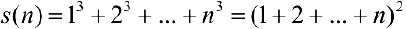 
. Тогда
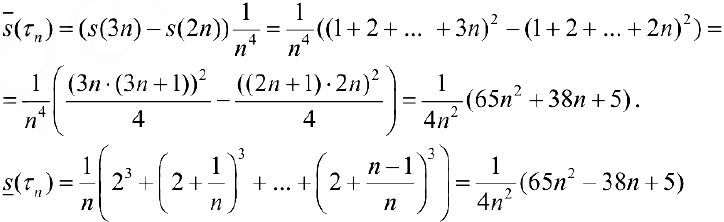
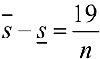
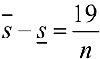. Пусть 
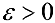, тогда если 
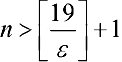, то соотношение (6) выполняется, поэтому 
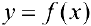интегрируема.
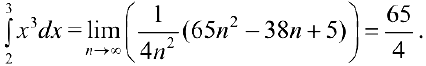
Теорема 2. а) Пусть функция 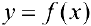— непрерывна на отрезке 
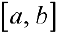. Тогда 
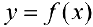— интегрируема на этом отрезке.
б) Пусть функция 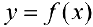— кусочно-непрерывна на отрезке 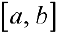(имеет на отрезке конечное число точек разрыва 1- ого рода). Тогда 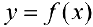интегрируема на этом отрезке. При этом 
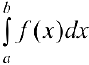не зависит от значений а функции в точках разрыва.
в) Пусть 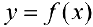— монотонна на отрезке 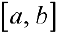, тогда 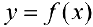— интегрируема на этом отрезке.
Задача №50.1.
Найти интеграл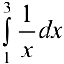 
, рассматривая его как предел интегральных сумм.
Решение:
Разобьем отрезок [1,3] на n отрезков так, чтобы точки образовывали геометрическую прогрессию:
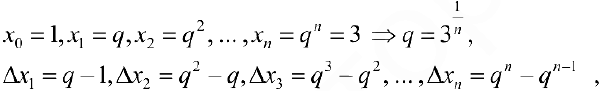
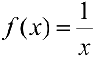монотонно убывает,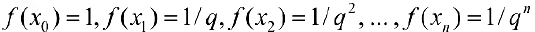 
Тогда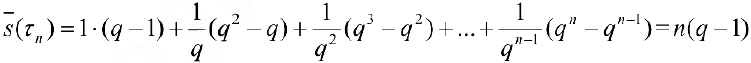 
и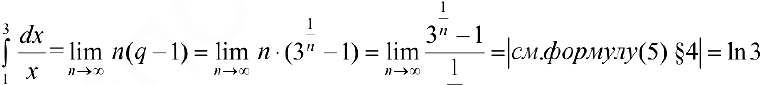 
Эта теория и задачи с решением взяты со страницы готовых задач с решением по математическому анализу:
Решение задач по математическому анализу
Возможно эти темы вам будут полезны:
