Оглавление:
Свойства функций B (a,b), Г (a)
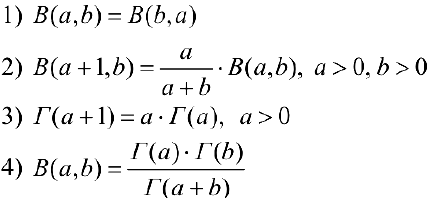
п.1. Докажем формулу (3).
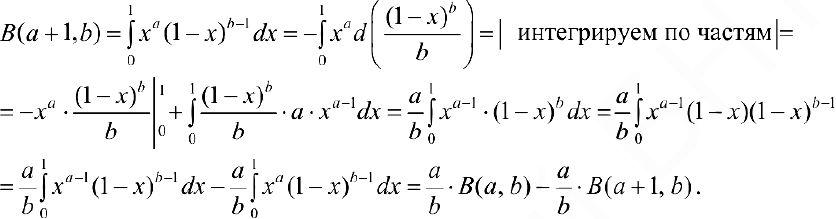
Из полученного уравнения:
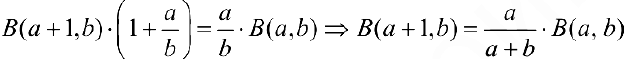, что и требовалось.
п.2. Докажем формулу (4).
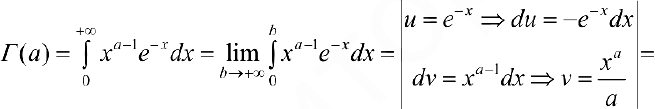
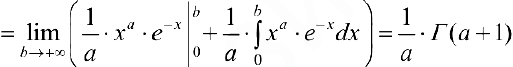
что и требовалось.
Так как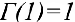 
то из формулы (4) следует, что 
,
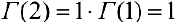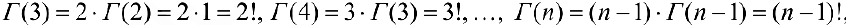
то есть
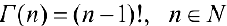
Аналогично, из формулы (3):
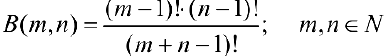
п.З. Преобразуем формулу (1):
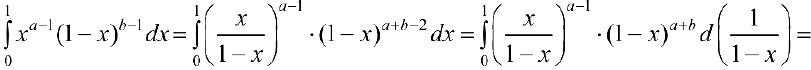
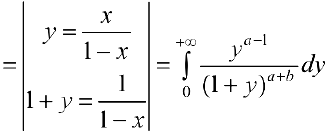— другое представление функции 
.
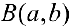Пусть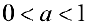 
, и пусть 
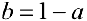, тогда
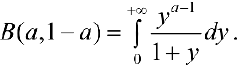
Можно показать, что интеграл в правой части формулы (8) сходится и его значение равно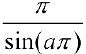 
. Таким образом
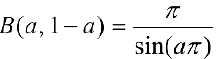
В частности,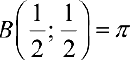 
, а из формулы (5):
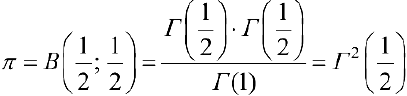, то есть
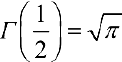
Далее, используя формулу (4):
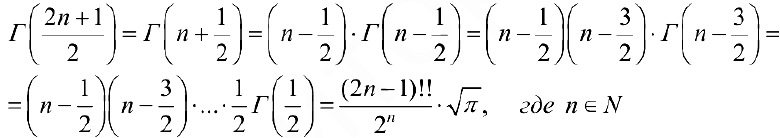
Из формул (9) и (5) следует:
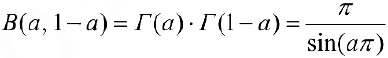
Задача №68
Найти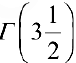 
.
Решение:
По формуле (11):
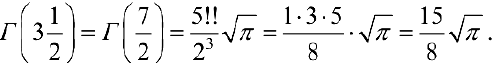
п.4. Перепишем формулу (4) в виде:
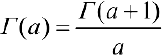
что позволяет доопределить функцию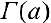 
для отрицательных значений 
:
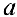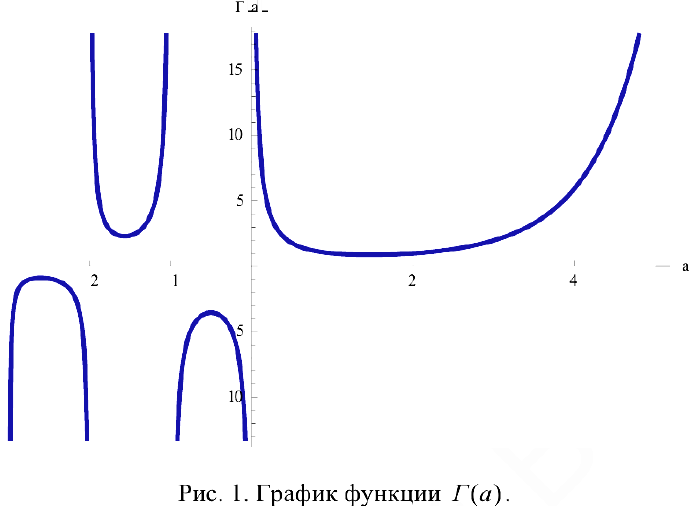
Задача №69
Найти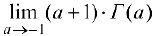 
.
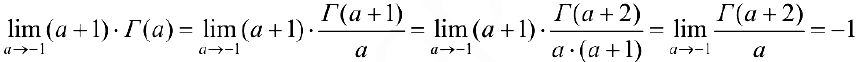
Задача №70
Вычислить интеграл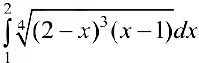 
.
Решение:
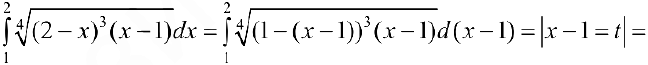
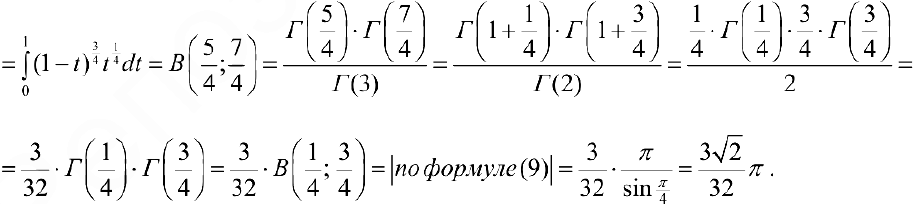
Упражнение 1. Вычислить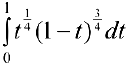 
, используя подстановки Чебышева (см.п.2, §22) .
п.5. Рассмотрим
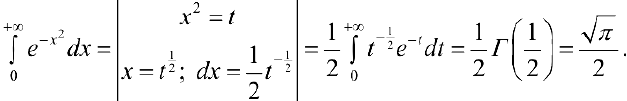
Поэтому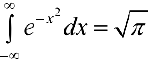 
— значение интеграла Пуассона.
Эта теория и задачи с решением взяты со страницы готовых задач с решением по математическому анализу:
Решение задач по математическому анализу
Возможно эти темы вам будут полезны:
