Оглавление:
Площадь поверхности вращения
Определение 1. Пусть L — простая кривая на плоскости заданная явно в виде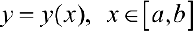 
(см. § 30). Пусть функция 
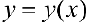— непрерывна и неотрицательна 
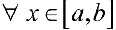. Разобьем отрезок 
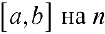частичных отрезков точками 
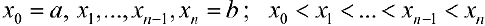и обозначим это разбиение 
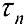. Пусть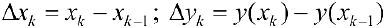 
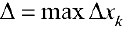— диаметр разбиения.
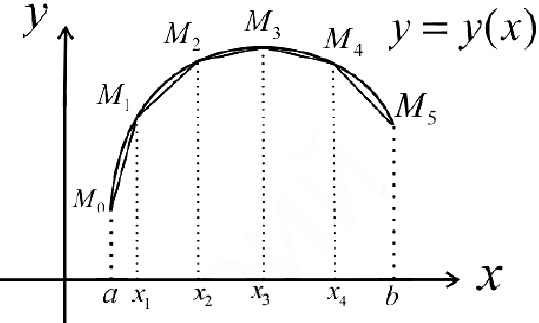
Пусть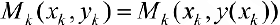 
точки на кривой 
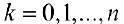. Рассмотрим ломаную последовательно проходящую через точки 
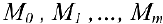При вращении кривой 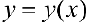вокруг оси 
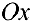каждое звено 
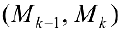ломаной описывает поверхность 
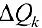. площадь которой 
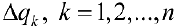(боковая поверхность усеченного конуса).
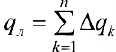площадь всей поверхности.
Если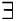 
предел при 
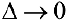площади 
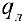не зависящий от способа разбиения отрезка, то он называется площадью q поверхности вращения кривой L вокруг оси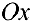
Таким образом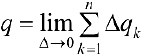 
Замечание. Пусть функция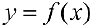 
— непрерывно-дифференцируема на отрезке 
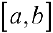, тогда 
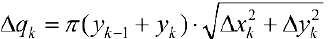— площадь боковой поверхности усеченного конуса; 
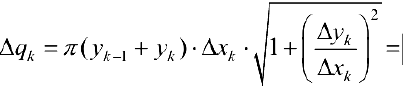(по теореме Лагранжа (см. теорему 4 § 12) 
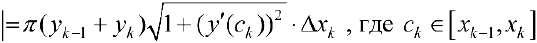. Поэтому
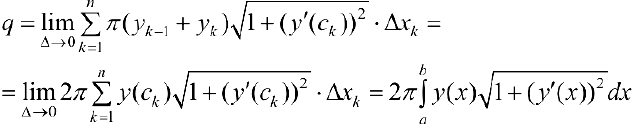
Таким образом:
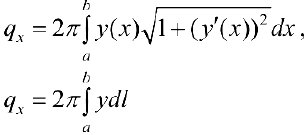
Где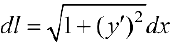 
— дифференциал дуги. Формулы (2) и (3) приведены для кривых L, лежащих выше оси 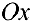. В общем случае верны формулы:
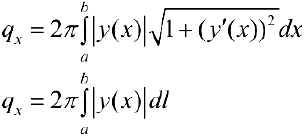
Если кривая L задала параметрически в виде
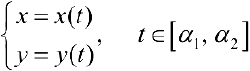то (см. § 32)
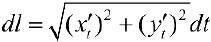, поэтому
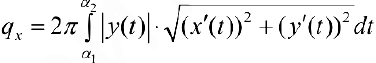
Для кривой L заданной в полярных координатах уравнением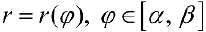 
, 
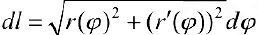, (см. § 32), и
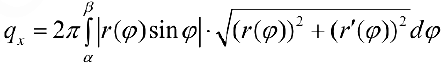
Задача №100
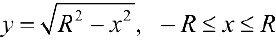— верхняя полуокружность радиуса R.
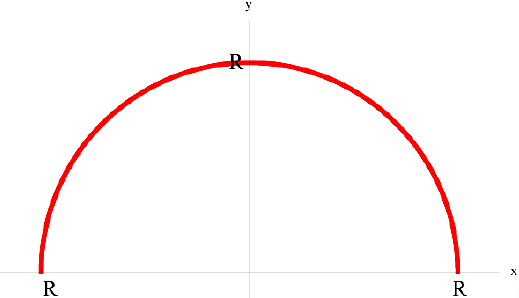
Найдем площадь поверхности при вращении вокруг оси .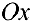
Решение:
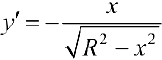, по формуле (2):
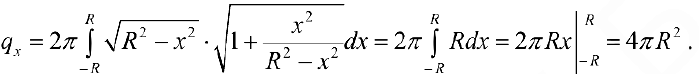
Задача №101
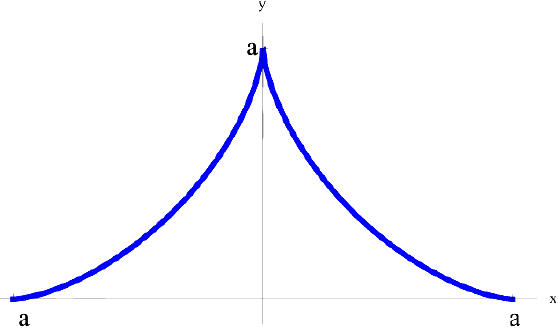
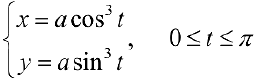— верхняя половина астроиды
Найдем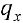 
.
Решение:
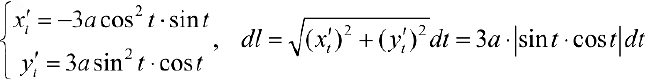(см. пример 1 § 32). Пусть 
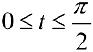, тогда по формуле (6):
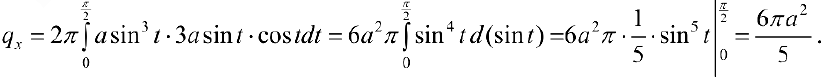
Поэтому площадь всей поверхности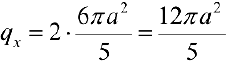 
.
Задача №102
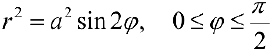— лепесток лемнискаты, расположенный в первой четверти
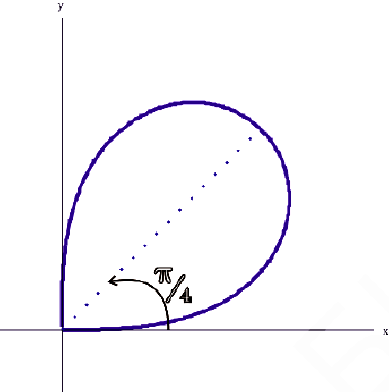
Найдем .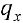
Решение:
.
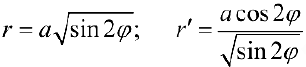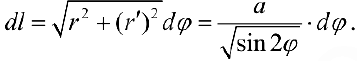. По формуле (7):
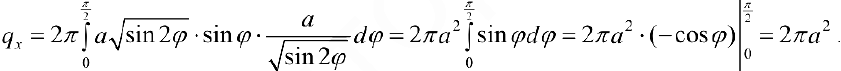
Эта теория и задачи с решением взяты со страницы готовых задач с решением по математическому анализу:
Решение задач по математическому анализу
Возможно эти темы вам будут полезны:
