Оглавление:
Определенный интеграл
Определение 1. Пусть функция 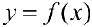 определена на отрезке
определена на отрезке 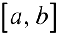 . Разобьем
. Разобьем 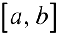 на n частичных отрезков точками
на n частичных отрезков точками 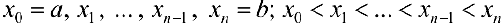 и обозначим это разбиение
и обозначим это разбиение 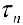 . Пусть
. Пусть 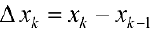 — длина k — ого частичного отрезка
— длина k — ого частичного отрезка 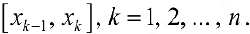 .
.
Число 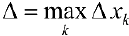 — диаметр разбиения. Выбираем на каждом отрезке
— диаметр разбиения. Выбираем на каждом отрезке 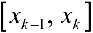 точку
точку 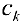 и составим сумму
и составим сумму
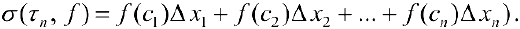
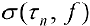 называется n — й интегральной суммой Римана.
называется n — й интегральной суммой Римана.
Функция 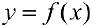 называется интегрируемой по Риману, если
называется интегрируемой по Риману, если 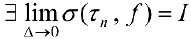 , то есть
, то есть 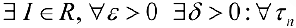 такого, что
такого, что 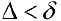 и
и 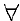 набора точек
набора точек 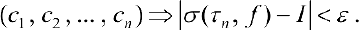
При этом 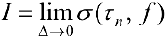 называется определенным интегралом от функции
называется определенным интегралом от функции 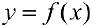 на отрезке
на отрезке 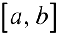 и обозначается
и обозначается 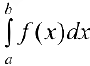 . Таким образом
. Таким образом
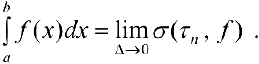
Будем считать, что 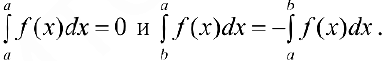 .
.
Задача №47
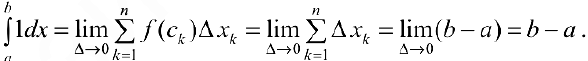
Задача №48
Пусть функция 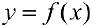 непрерывна на отрезке
непрерывна на отрезке 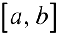 ,
, 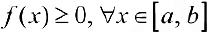 . Рассмотрим фигуру Ф на плоскости:
. Рассмотрим фигуру Ф на плоскости:
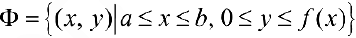 — криволинейную трапецию:
— криволинейную трапецию:
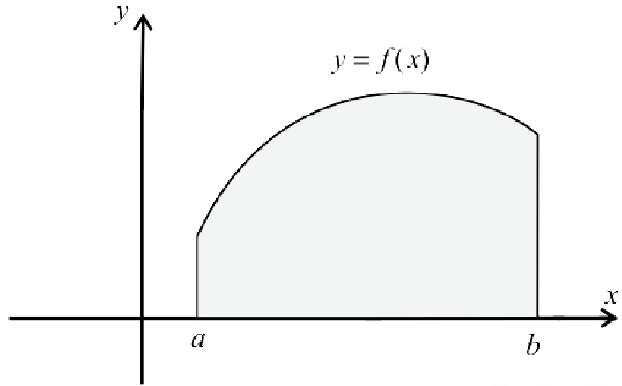
Рис.1 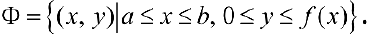
Пусть 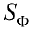 — ее площадь. Из (1) следует, что
— ее площадь. Из (1) следует, что 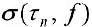 равна площади ступенчатой фигуры, составленной из прямоугольников с основаниями
равна площади ступенчатой фигуры, составленной из прямоугольников с основаниями 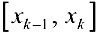 и высотами
и высотами 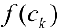 :
:
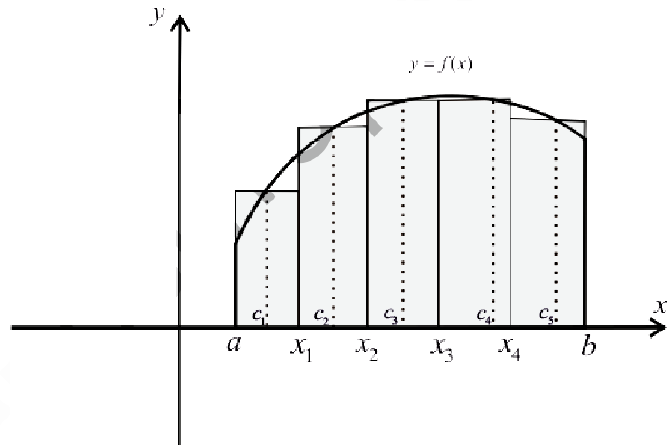
Рис. 2. Интегральная сумма 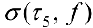
Тогда 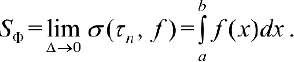 .
.
Теорема 1. (необходимое условие интегрируемости функции).
Пусть 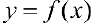 — интегрируема на отрезке
— интегрируема на отрезке 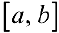 , тогда
, тогда 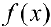 — ограничена на
— ограничена на 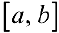 .
.
Доказательство. Предположим, что 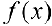 — неограничена на
— неограничена на 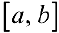 . Пусть
. Пусть 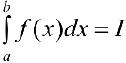 и пусть
и пусть 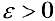 . Из (2) следует, что 3 8 — 8(e), такое что
. Из (2) следует, что 3 8 — 8(e), такое что
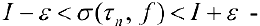
для любой 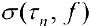 у которой
у которой 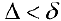 , то есть эти интегральные суммы
, то есть эти интегральные суммы 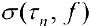 — ограничены. Причем неравенство (4) выполнено при любом выборе точек
— ограничены. Причем неравенство (4) выполнено при любом выборе точек 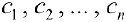 из соответствующих отрезков. Пусть
из соответствующих отрезков. Пусть 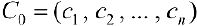 — один из таких наборов точек. Так как
— один из таких наборов точек. Так как 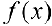 — неограничена на
— неограничена на 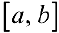 , то она неограниченна по крайней мере на одном из частичных отрезков. Пусть, например, это будет отрезок
, то она неограниченна по крайней мере на одном из частичных отрезков. Пусть, например, это будет отрезок 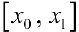 . Рассмотрим наборы
. Рассмотрим наборы 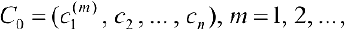 где
где 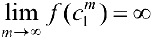 , тогда, так как
, тогда, так как  -фиксированы, то, начиная с какого-то номера
-фиксированы, то, начиная с какого-то номера 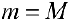 , суммы (1) будут выходить за пределы промежутка (4). Противоречие.
, суммы (1) будут выходить за пределы промежутка (4). Противоречие.
Замечание. Условие теоремы 1 необходимо, но не достаточно для интегрируемости функции.
Задача №49
Рассмотрим функцию Дирихле
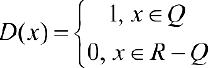 (см. пример 3 §5) на отрезке
(см. пример 3 §5) на отрезке 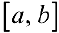 .
.
Тогда 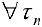 сумма
сумма 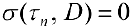 , если числа
, если числа 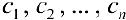 — иррациональные, и
— иррациональные, и 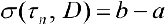 , если
, если 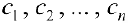 — рациональные. Поэтому
— рациональные. Поэтому 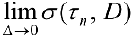 — не существует и функция
— не существует и функция 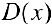 — неинтегрируема.
— неинтегрируема.
Определение 2. Пусть функция 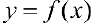 определена на отрезке
определена на отрезке 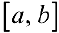 и ограничена па этом отрезке. Пусть
и ограничена па этом отрезке. Пусть 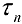 — разбиение отрезка
— разбиение отрезка 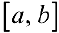 .
.
Пусть 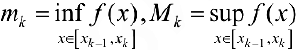 , тогда
, тогда
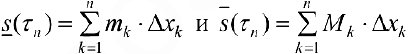
называются нижней и верхней суммой Дарбу для функции 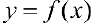 .
.
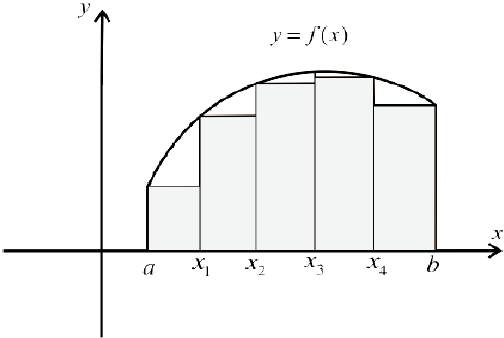
Рис.3.Нижняя сумма Дарбу 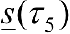 .
.
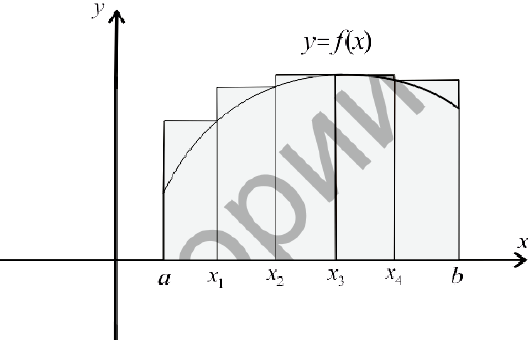
Рис.4.Верхняя сумма Дарбу 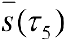 .
.
Суммы Дарбу являются функциями, определенными на множестве всех разбиений 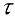 отрезка
отрезка 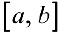 .
.
Эта теория и задачи с решением взяты со страницы готовых задач с решением по математическому анализу:
Решение задач по математическому анализу
Возможно эти темы вам будут полезны:

