Оглавление:
Объемы тел
Под телом Т будем подразумевать ограниченное множество в пространстве. Будем рассматривать тела, имеющие внутренние точки и границу, которая также принадлежит телу (замкнутые тела), причем такие, что любые две внутренние точки можно соединить непрерывной линией, проходящей внутри тела.
Определение 1. Рассмотрим тело 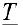 составленное из конечного числа многогранников, содержащихся в Т, и тело
составленное из конечного числа многогранников, содержащихся в Т, и тело 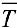 , составленное из многогранников и покрывающее тело
, составленное из многогранников и покрывающее тело 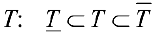
Пусть 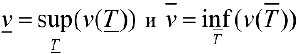 , где
, где 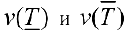 объемы тел
объемы тел 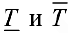 . Тело называется кубируемым, если
. Тело называется кубируемым, если 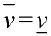 . При этом число
. При этом число
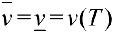
называется объемом тела Т (по Жордану).
Замечание. Для кубируемости тела Т необходимо и достаточно, чтобы 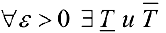 такие, что
такие, что
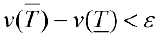
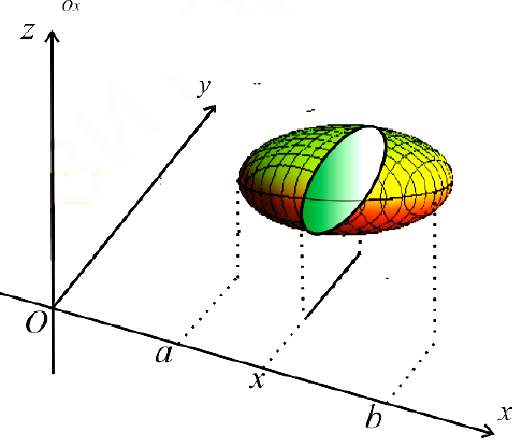
Пусть для кубируемого тела Т известны площади 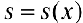 его сечения плоскостями перпендикулярными оси Ох, проходящими через точки
его сечения плоскостями перпендикулярными оси Ох, проходящими через точки 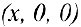 ,
, 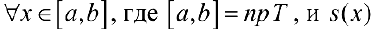 — непрерывна
— непрерывна
Разобьем отрезок 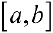 па и частичных отрезков точками
па и частичных отрезков точками 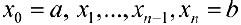 ;
; 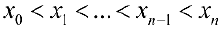 и обозначим это разбиение
и обозначим это разбиение 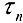 . Пусть
. Пусть 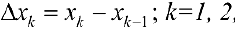 ,
,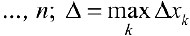 , — диаметр разбиения, тогда
, — диаметр разбиения, тогда
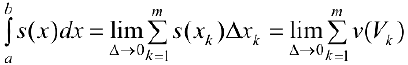
Где 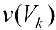 это — объем цилиндрического тела высотой
это — объем цилиндрического тела высотой 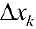 . и площадью основания
. и площадью основания 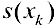 . Пусть
. Пусть 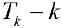 -ый слой тела Т между плоскостями, проходящими через точки
-ый слой тела Т между плоскостями, проходящими через точки 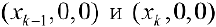 и перпендикулярными оси Ох.
и перпендикулярными оси Ох.
Так как Т — кубируемо, то 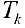 — также кубируемо и
— также кубируемо и 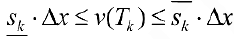 , где
, где
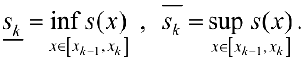
Тогда
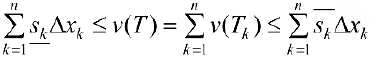
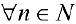 , или
, или
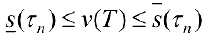
Где 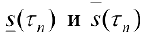 это — нижняя и верхняя суммы Дарбу функции ,
это — нижняя и верхняя суммы Дарбу функции , 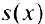 для разбиения
для разбиения  . Поэтому
. Поэтому 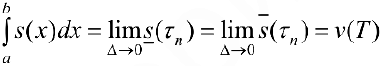 . Таким образом
. Таким образом
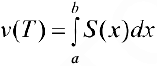
Замечание. Нужно заметить, что неравенство (4), которое использовалось для вывода формулы (6), выполняется, когда любые два рассматриваемые сечения тела Т при проекции на плоскость yOz полностью содержатся одно в другом. Однако формула (6) верна и в общем случае. Для этого достаточно потребовать, чтобы тело Т было кубируемым и функция 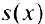 — непрерывной.
— непрерывной.
Задача №92
Найти объем тела ограниченного поверхностями 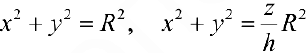 (ниже параболоида).
(ниже параболоида).
Решение:
Из системы уравнений 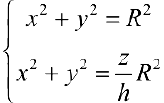 следует, что z = h.
следует, что z = h.
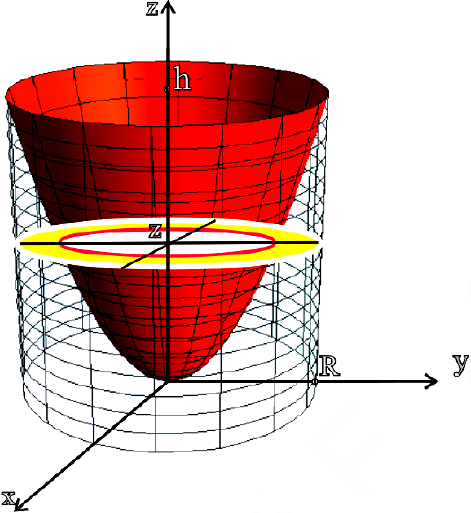
В сечении тела плоскостью проходящей через точку 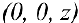 перпендикулярно оси Oz получается кольцо
перпендикулярно оси Oz получается кольцо
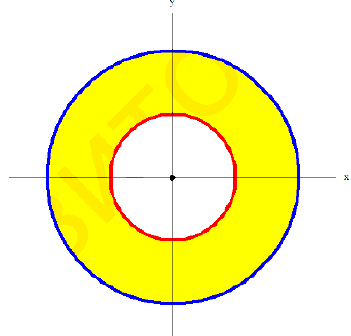
Радиус внешней окружности равен R. радиус внутренней равен 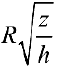 .
.
Поэтому по формуле (6):
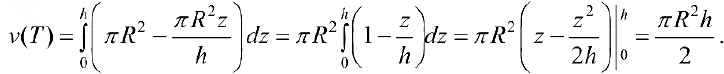
Формулу (6) удобно применять к телам вращения. Пусть 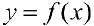 — непрерывна на отрезке
— непрерывна на отрезке 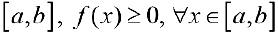 . Будем вращать криволинейную трапецию
. Будем вращать криволинейную трапецию
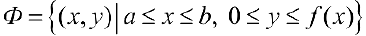
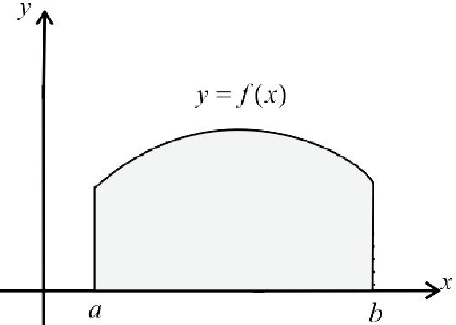
вокруг оси Ох. Получим тело:
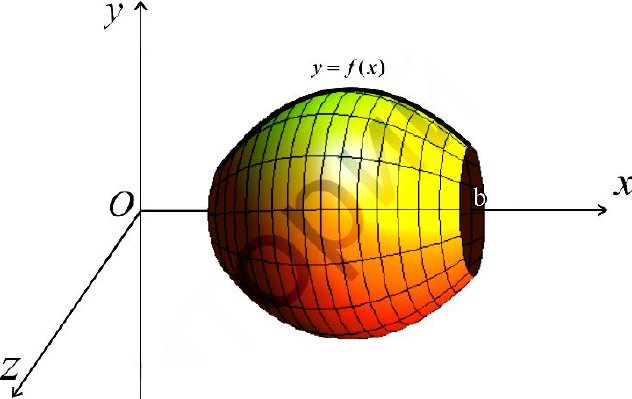
Тогда сечением полученного тела плоскостью проходящей через точку (х, 0,0) и перпендикулярной оси Ох будет круг радиуса 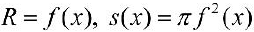 , и по формуле (6):
, и по формуле (6):
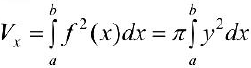
Где 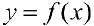 .
.
Аналогично, если 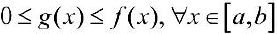 , то при вращении вокруг оси Ох фигуры
, то при вращении вокруг оси Ох фигуры 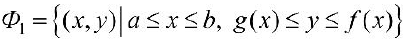
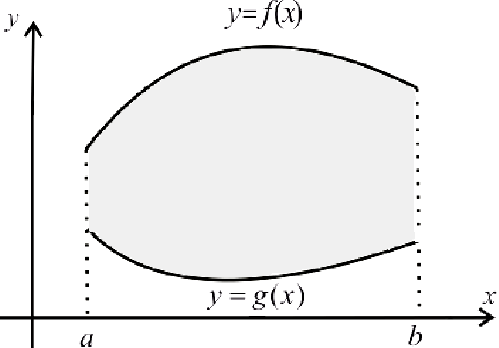
Получим тело, объем которого
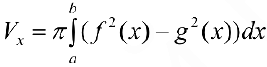
Задача №93
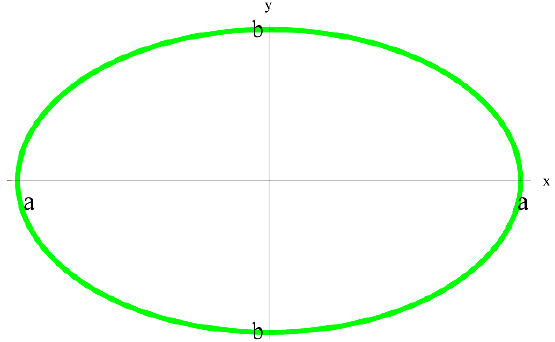
Рассмотрим фигуру Ф ограниченную эллипсом 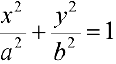 ,
, 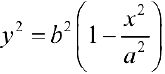 . Найдем объем эллипсоида полученного при вращении вокруг оси Ох фигуры Ф .
. Найдем объем эллипсоида полученного при вращении вокруг оси Ох фигуры Ф .
Решение:
По формуле (7): 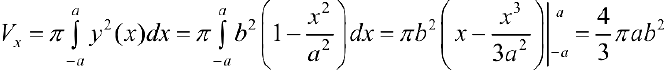 .
.
Пусть функция 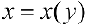 — непрерывна при
— непрерывна при 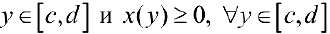 . Тогда, аналогично, при вращении вокруг оси Оу фигуры
. Тогда, аналогично, при вращении вокруг оси Оу фигуры
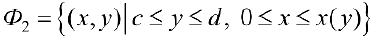
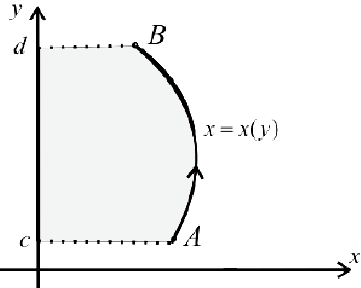
Получим тело, объем которого
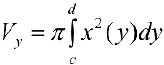
Если же вращать вокруг оси Оу трапецию
то 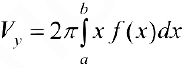
Задача №94
Рассмотрим тело Т из примера 1. Оно получается, если вращать вокруг оси Oz фигуру, ограниченную линиями:
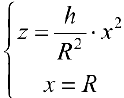
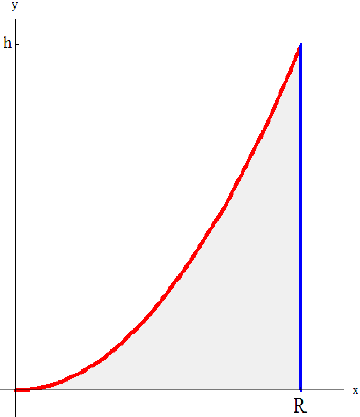
Из первого уравнения найдем 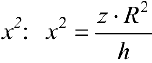 , поэтому по формуле (9):
, поэтому по формуле (9):
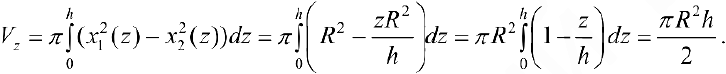
Задача №95
Объем 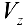 при вращении фигуры
при вращении фигуры 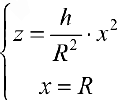 из примера 3 вокруг оси Oz можно также найти и по формуле (10):
из примера 3 вокруг оси Oz можно также найти и по формуле (10):
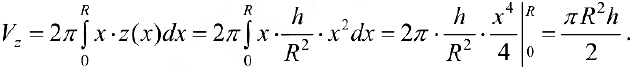
Задача №96
Фигура Ф ограничена линиями 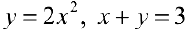 . Найти
. Найти 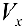 .
.
Решение:
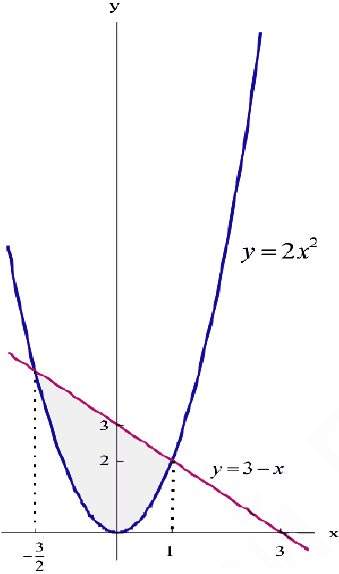
Абсциссы точек пересечения: 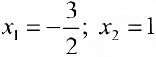 (см. пример 1 § 30). По формуле (8):
(см. пример 1 § 30). По формуле (8):
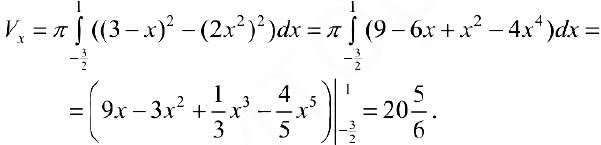
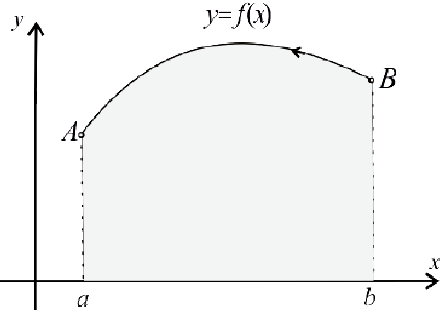
Замечание. Для непрерывной функции 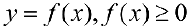 рассмотрим криволинейную трапецию
рассмотрим криволинейную трапецию 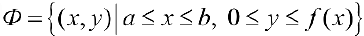
Пусть 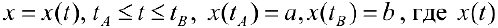 — непрерывно-дифференцируема на промежутке
— непрерывно-дифференцируема на промежутке 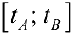 . Тогда по формуле (7):
. Тогда по формуле (7): 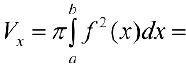
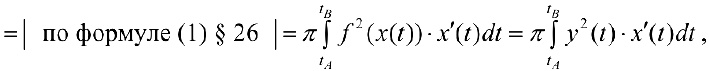
Где 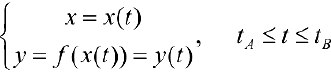 — параметрическое задание линии
— параметрическое задание линии
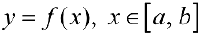 . Таким образом —
. Таким образом — 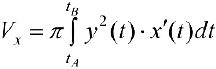 , или
, или
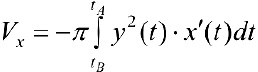
(кривая обходится так, чтобы область Ф оставалась слева).
Аналогично, для непрерывной функции 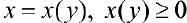 рассмотрим криволинейную трапецию
рассмотрим криволинейную трапецию 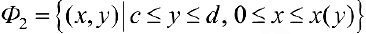
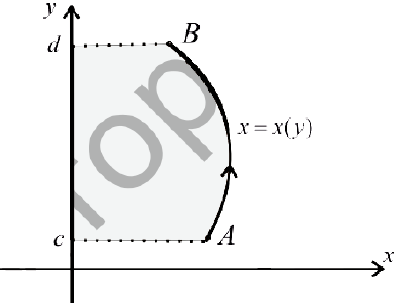
Пусть 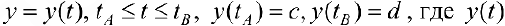 — непрерывно-дифференцируема на промежутке
— непрерывно-дифференцируема на промежутке 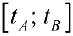 . Тогда по формуле (9):
. Тогда по формуле (9):
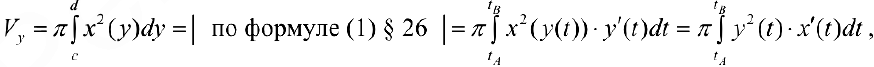
Где 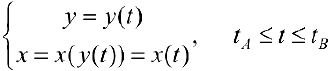 — параметрическое задание линии
— параметрическое задание линии
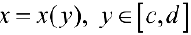 . Таким образом
. Таким образом
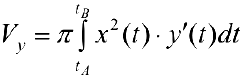
(кривая обходится так, чтобы область Ф оставалась слева).
Рассмотрим область ограниченную простой замкнутой кривой 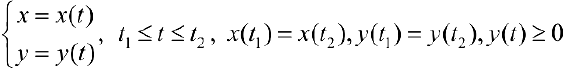 (кривая лежит по одну сторону от оси Ох). Тогда объем
(кривая лежит по одну сторону от оси Ох). Тогда объем 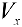 можно находить по формуле (12):
можно находить по формуле (12):
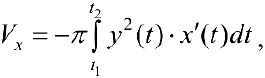
(кривая обходится так, чтобы область оставалась слева).
Аналогично ,для области ограниченной простой замкнутой кривой 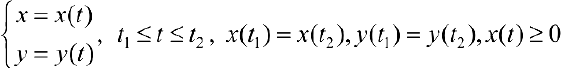 (кривая лежит по одну сторону от оси (Оу) объем
(кривая лежит по одну сторону от оси (Оу) объем 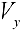 можно находить по формуле (13):
можно находить по формуле (13):
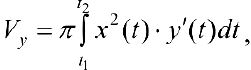
(кривая обходится так, чтобы область оставалась слева).
Задача №97
Дана астроида 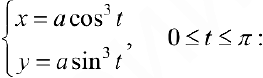
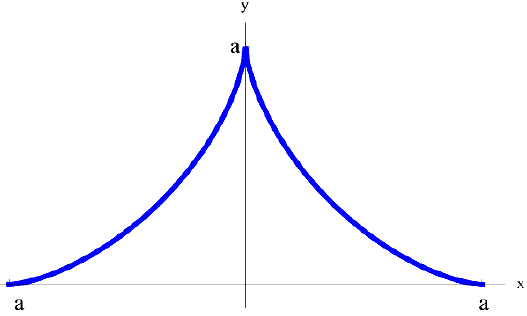
Найдем 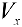 .
.
Решение:
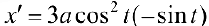 , по формуле (12):
, по формуле (12):
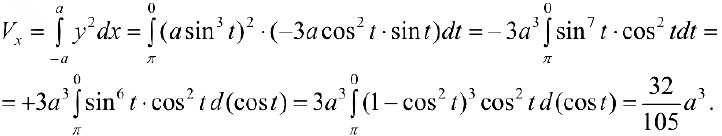
Задача №98
Петля кривой 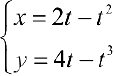 вращается вокруг оси Ох .Найти
вращается вокруг оси Ох .Найти  .
.
Решение:
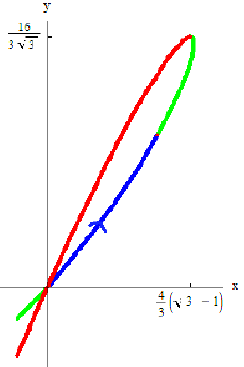
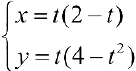 , при
, при 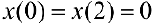 и
и 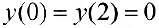 ,при
,при 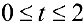 петля обходится против часовой стрелки. По формуле (12):
петля обходится против часовой стрелки. По формуле (12):
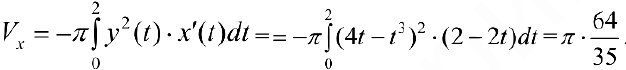
Упражнение 3. Петля кривой 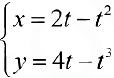 . вращается вокруг оси Оу. Найти
. вращается вокруг оси Оу. Найти 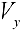 .
.
Пусты 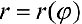 — кривая в полярной системе координат,
— кривая в полярной системе координат, 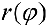 — непрерывна при
— непрерывна при 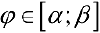 . Рассмотрим па плоскости
. Рассмотрим па плоскости  криволинейный сектор
криволинейный сектор 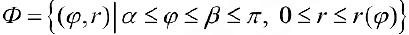
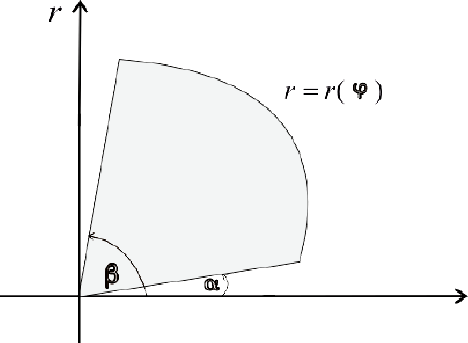
Тогда объем тела при вращении фигуры 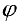 вокруг полярной оси равен
вокруг полярной оси равен
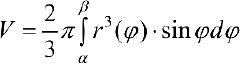
Задача №99
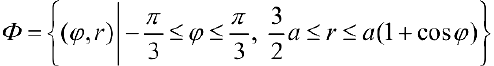 (см. пример 4 § 31).
(см. пример 4 § 31).
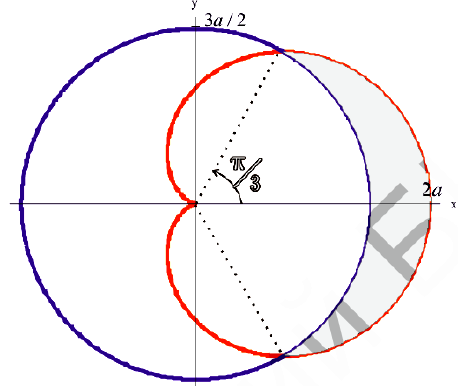
Найдем 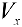 .
.
Решение:
По формуле (14):
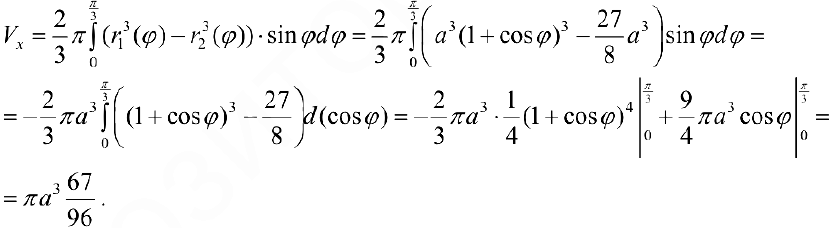
Эта теория и задачи с решением взяты со страницы готовых задач с решением по математическому анализу:
Решение задач по математическому анализу
Возможно эти темы вам будут полезны:

