Оглавление:
Несобственные интегралы первою рода
Несобственный интеграл первого рода — обобщение понятия интеграла Римана на бесконечный промежуток. Для бесконечного промежутка  составить суммы Римана вида (1) § 24 нельзя.
составить суммы Римана вида (1) § 24 нельзя.
Определение 1. Пусть функция 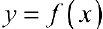 определена на промежутке
определена на промежутке 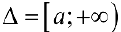 и интегрируема на любом конечном отрезке
и интегрируема на любом конечном отрезке 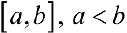 . Несобственным интегралом 1 -го рода функции
. Несобственным интегралом 1 -го рода функции 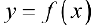 па промежутке
па промежутке  называется
называется 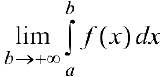 . Несобственный интеграл обозначается
. Несобственный интеграл обозначается 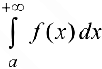 .
.
Таким образом:
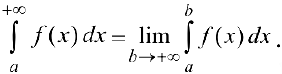
Если предел (1) существует, то интеграл называется сходящимся, в противном случае — расходящимся.
Аналогично:
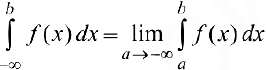
для функции 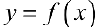 , определенной на промежутке
, определенной на промежутке 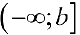 и интегрируемой на любом конечном промежутке
и интегрируемой на любом конечном промежутке 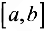 и
и
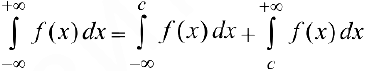
где с — промежуточная точка , и интегралы в правой части формулы (3) вычисляются по формулам (1) и (2).
+? dx г dx 1 х 1 Ь л
Задача №57
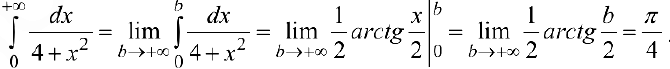
Задача №58
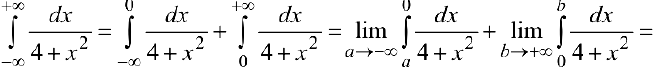
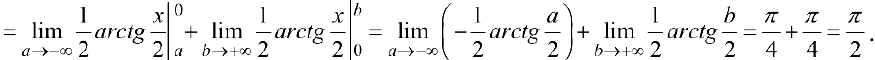
Задача №59
Исследовать па сходимость 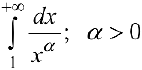
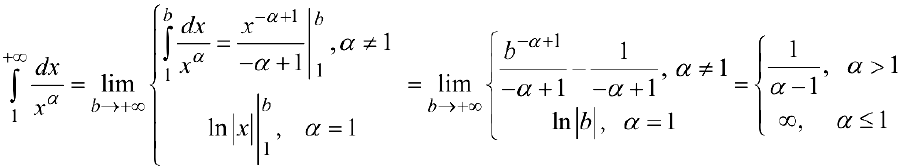
Таким образом, интеграл сходится, если 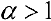 и расходится, если
и расходится, если 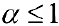 .
.
Теорема 1 (признак сравнения). Пусть функции 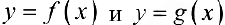 определены на промежутке
определены на промежутке 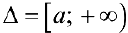 , интегрируемы на любом конечном промежутке
, интегрируемы на любом конечном промежутке 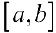 и пусть
и пусть 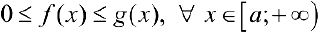 .
.
Тогда из сходимости 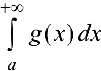 следует сходимость
следует сходимость 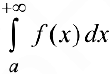 , а из расходимости
, а из расходимости 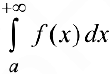 следует расходимость
следует расходимость 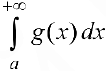 .
.
Доказательство следует из неравенства;
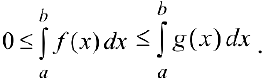
Теорема 2 (предельный признак сравнения). Пусть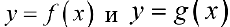 положительны
положительны 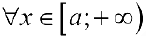 , удовлетворяют условиям определения 1 па этом промежутке и
, удовлетворяют условиям определения 1 па этом промежутке и 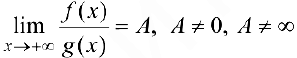 . Тогда
. Тогда 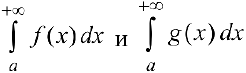 сходятся или расходятся одновременно.
сходятся или расходятся одновременно.
Доказательство. Пусть 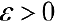 и такое, что
и такое, что 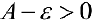 , тогда из определения предела
, тогда из определения предела 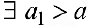 такое, что
такое, что
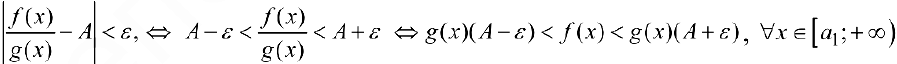
И далее доказательство следует из теоремы 1.
На практике, при исследовании на сходимость по предельному признаку в качестве 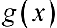 часто используют функцию
часто используют функцию 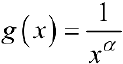 .
.
Задача №60
Исследовать на сходимость интеграл 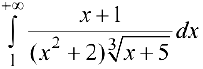 .
.
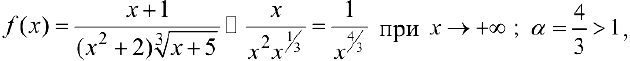 , следовательно, (см. пример 3), интеграл сходится.
, следовательно, (см. пример 3), интеграл сходится.
Определение 2. Несобственный интеграл 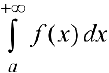 называется абсолютно-сходящимся, если сходится интеграл
называется абсолютно-сходящимся, если сходится интеграл 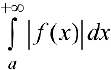 .
.
Несобственный интеграл 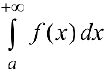 называется условно-сходящимся, если
называется условно-сходящимся, если 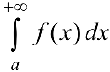 сходится, а интеграл
сходится, а интеграл 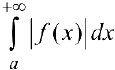 — расходится.
— расходится.
Теорема 3. Пусть 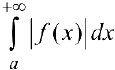 — сходится, тогда
— сходится, тогда 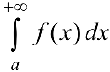 — также сходится.
— также сходится.
Доказательство. Пусть 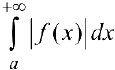 . сходится, тогда по критерию Коши (см.теорему 5 § 3)
. сходится, тогда по критерию Коши (см.теорему 5 § 3) 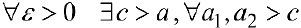 выполняется неравенство
выполняется неравенство
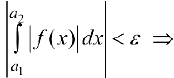 по свойству 4 § 24:
по свойству 4 § 24: 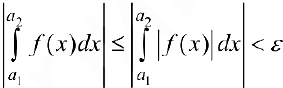 и по критерию Коши
и по критерию Коши 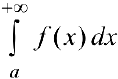 — сходится.
— сходится.
Задача №61
Исследовать на абсолютную и условную сходимость J у«х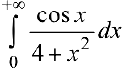
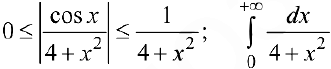 — сходится, (см. пример 1), тогда по признаку сравнения
— сходится, (см. пример 1), тогда по признаку сравнения 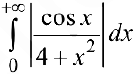 . сходится и, следовательно,
. сходится и, следовательно, 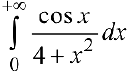 сходится абсолютно.
сходится абсолютно.
Задача №62
Исследовать на абсолютную и условную сходимость интегралы
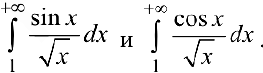
п.1. Исследуем интегралы на сходимость.
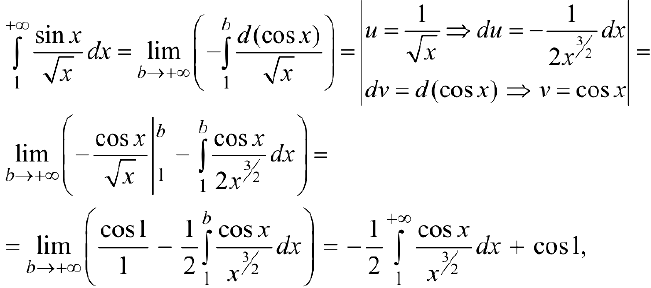
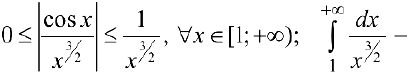 — сходится,
— сходится, 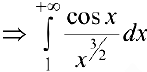 сходится и, следовательно, сходится
сходится и, следовательно, сходится 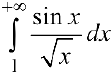
Аналогично: 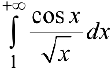 — сходится.
— сходится.
n.2. Исследуем интеграл 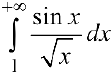 па абсолютную сходимость:
па абсолютную сходимость:
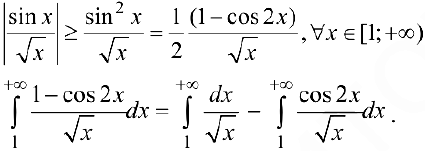
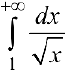 расходится,
расходится, 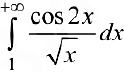 — сходится (согласно п. 1), поэтому
— сходится (согласно п. 1), поэтому 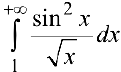 — расходится, => по признаку сравнения
— расходится, => по признаку сравнения 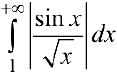 — расходится, поэтому
— расходится, поэтому 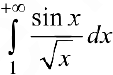 сходится условно.
сходится условно.
Аналогично: 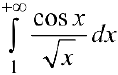 — сходится условно.
— сходится условно.
Задача №63
Исследовать на абсолютную и условную сходимость интегралы 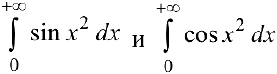 — интегралы Френеля.
— интегралы Френеля.
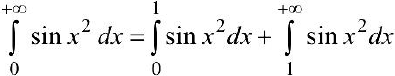 . Рассмотрим
. Рассмотрим
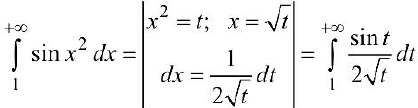 сходится условно (см. пример 6). поэтому и
сходится условно (см. пример 6). поэтому и 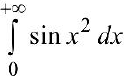 сходится условно.
сходится условно.
Аналогично 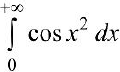 — сходится условно.
— сходится условно.
Значения интегралов: 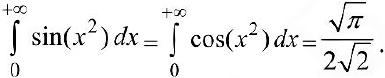 .
.
Замечание. Функции 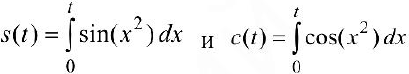 также называемые интегралами Френеля используются в оптике;
также называемые интегралами Френеля используются в оптике; 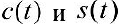 через элементарные функции не выражаются.
через элементарные функции не выражаются.
Упражнение 1. Графики функций 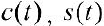 :
:
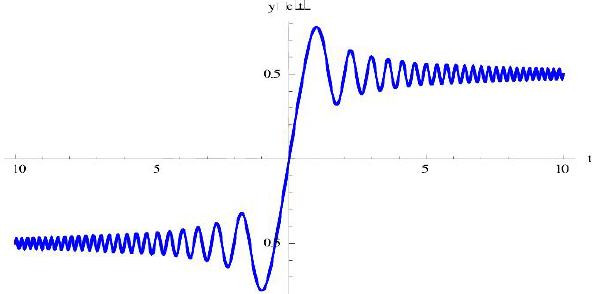
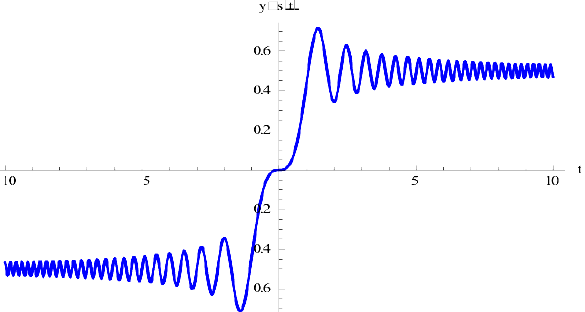
Построить графики функций 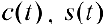 , используя пакет Mathematica (рассмотреть стандартные функции
, используя пакет Mathematica (рассмотреть стандартные функции 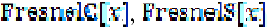 ).
).
Замечание. Кривая, заданная параметрически в виде: 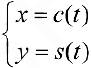 называется клотоидой (спиралью Корню).
называется клотоидой (спиралью Корню).
Используется при проектировании и строительстве дорог и транспортных развязок (угловое ускорение машины, движущейся по кривой с постоянной скоростью, равно пулю).
Упражнение 2. График клотоиды 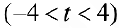 :
:
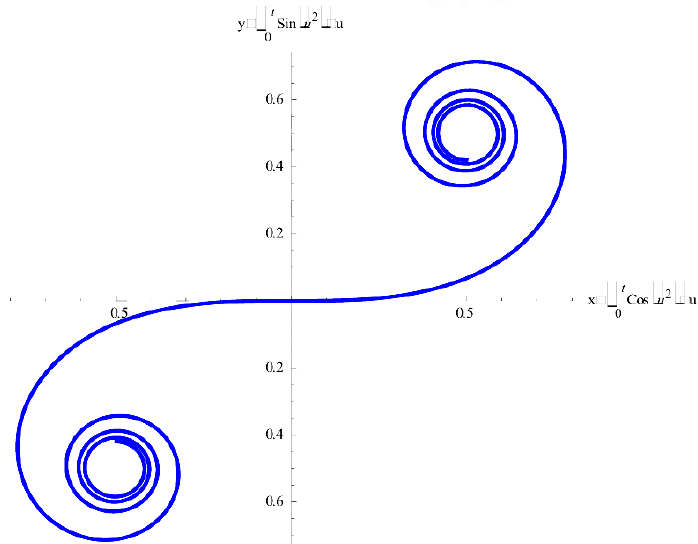
Построить график клотоиды: 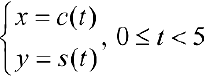 в пакете Mathematica.
в пакете Mathematica.
Упражнение 3. Исследовать на абсолютную и условную сходимость интегралы 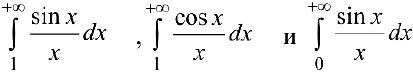
Замечание. 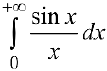 называется интегралом Дирихле;
называется интегралом Дирихле; 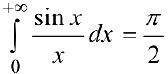 .
.
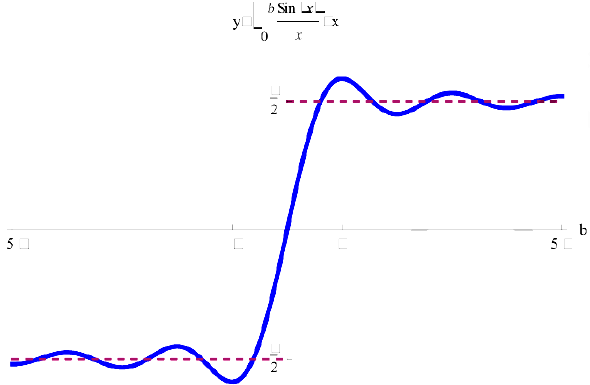
Рис. 1. График функции 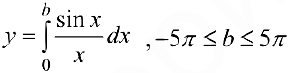 .
.
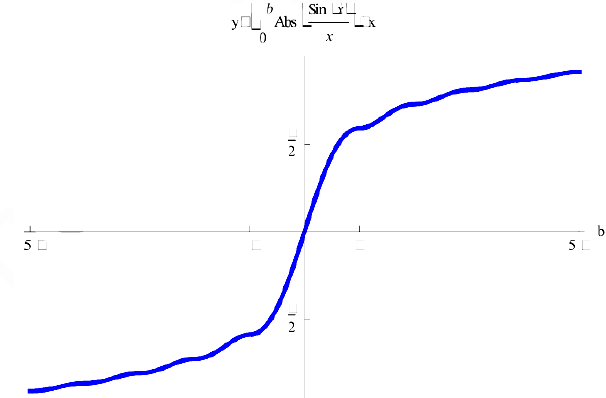
Рис.2. График функции 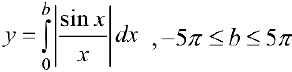 .
.
Интегралы Дирихле и Френеля являются примерами интегралов от функций, первообразные которых не выражаются через элементарные функции.
Еще один такой пример — интеграл Пуассона (Эйлера-Пуассона или Гауссов интеграл): 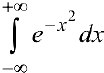 . Интеграл сходится и
. Интеграл сходится и 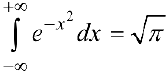 .
.
Эта теория и задачи с решением взяты со страницы готовых задач с решением по математическому анализу:
Решение задач по математическому анализу
Возможно эти темы вам будут полезны:

