Оглавление:
Интегрирование рациональных дробей
Определение 1. Рациональной дробью называется произвольная функция вида:
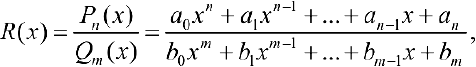
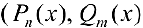
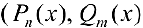 — многочлены степени n и m). Дробь
— многочлены степени n и m). Дробь 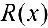 — правильная, если
— правильная, если 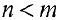 .
.
Если  , то
, то 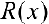 — неправильная дробь.
— неправильная дробь.
Элементарными рациональными дробями называются дроби вида:
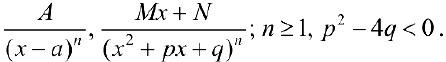
Интегрирование элементарных дробей.
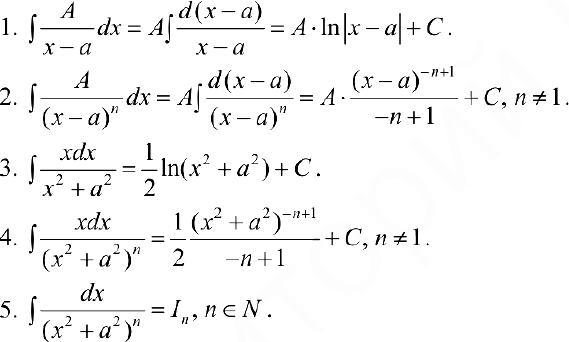
Найдем рекуррентную формулу для вычисления 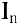 .
.
Пусть 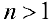 .
.
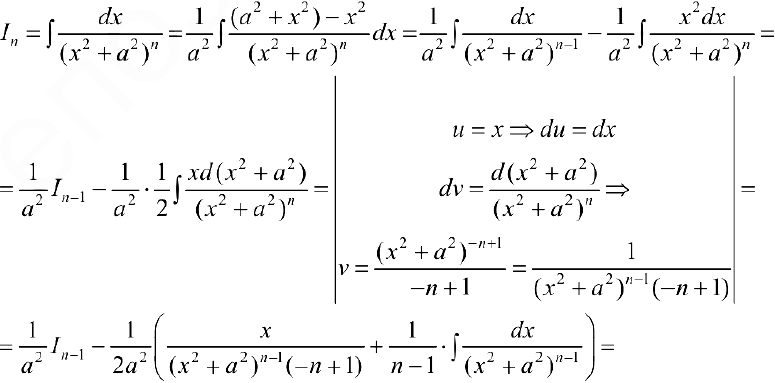
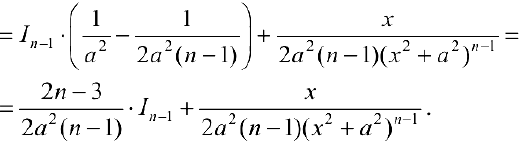
Вычисление интегралов 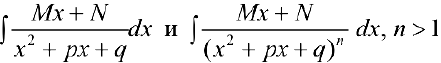 сведется к случаям 3-5, если выделить полный квадрат в трехчлене
сведется к случаям 3-5, если выделить полный квадрат в трехчлене 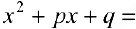
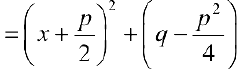 и сделать подстановку
и сделать подстановку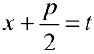
Задача №26
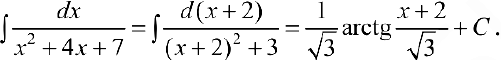
Задача №27
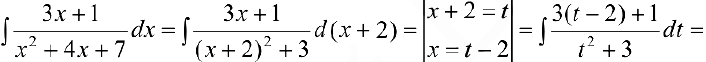
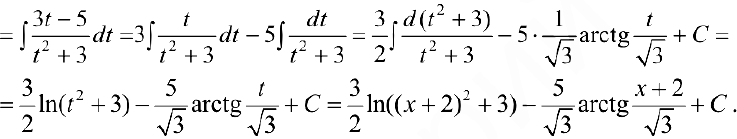
Задача №28
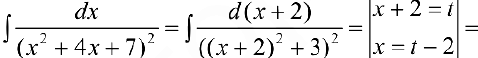
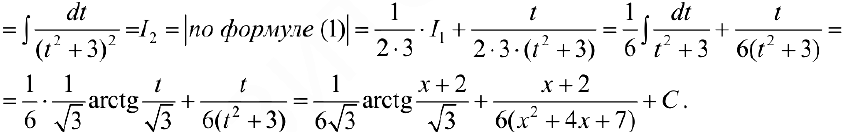
Теорема 1. Рассмотрим правильную рациональную дробь:
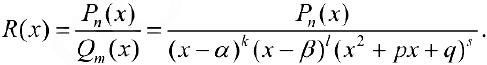
Дробь 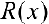 можно единственным образом разложить в сумму элементарных дробей:
можно единственным образом разложить в сумму элементарных дробей:
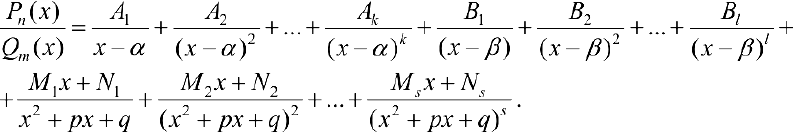
Коэффициенты 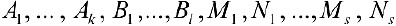 находятся, если правую часть равенства (2) привести к общему знаменателю и приравнять числители правой и левой части. Если дробь
находятся, если правую часть равенства (2) привести к общему знаменателю и приравнять числители правой и левой части. Если дробь 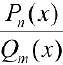 — неправильная, то делят
— неправильная, то делят 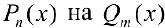 уголком и представляют дробь в виде:
уголком и представляют дробь в виде:
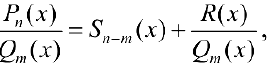
где 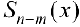 — частное,
— частное, 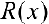 — остаток.
— остаток.
Задача №29
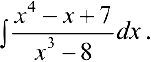 Дробь
Дробь 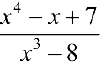 — неправильная. По формуле (3):
— неправильная. По формуле (3):
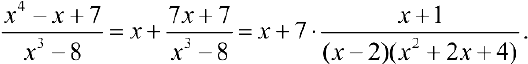
По формуле (2):
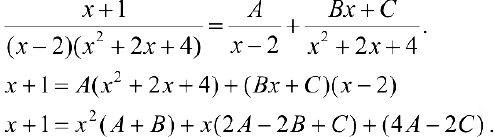
Для того, чтобы равенство (4) выполнялось 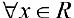 необходимо, чтобы равнялись друг другу коэффициенты при одинаковых степенях х.
необходимо, чтобы равнялись друг другу коэффициенты при одинаковых степенях х.
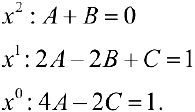
Решив систему уравнений (5), получим:
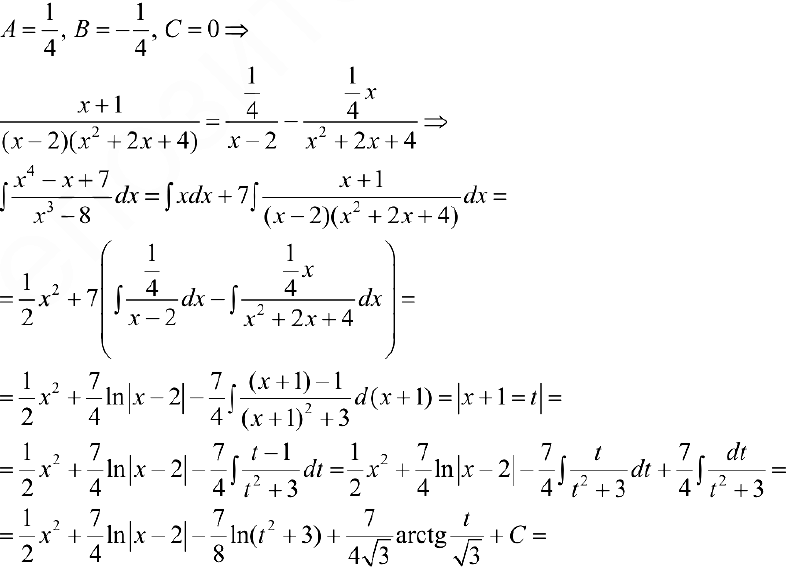
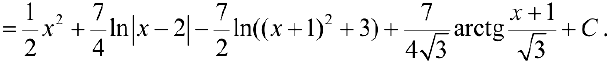
Если корни знаменателя 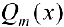 — действительны и имеют кратности 1, то коэффициенты в формуле (2) можно найти более простым способом.
— действительны и имеют кратности 1, то коэффициенты в формуле (2) можно найти более простым способом.
Задача №30
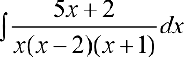
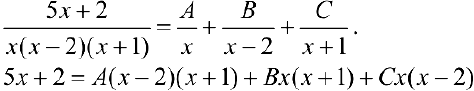
Подставляя в правую и левую части равенства конкретные значения х, получим:
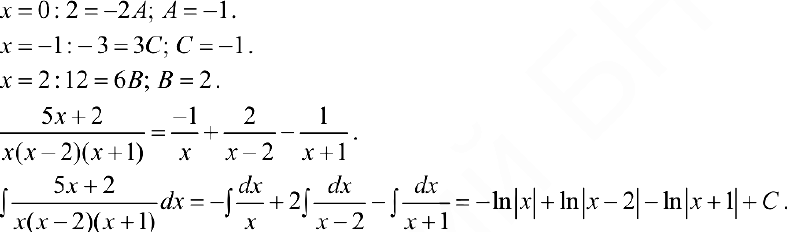
Эта теория и задачи с решением взяты со страницы готовых задач с решением по математическому анализу:
Решение задач по математическому анализу
Возможно эти темы вам будут полезны:

