Оглавление:
Интегрирование по частям в неопределенном интеграле
Теорема 1. Пусть функция 
— дифференцируемы на промежутке 
и на этом промежутке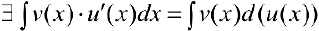 
. Тогда на этом промежутке 
и
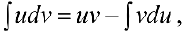
формула интегрирования по частям.
Доказательство. 
; (см. § 6).
(по свойству 1 § 18), 
существует по условию теоремы, поэтому 
— существует и 
.
Задача №22
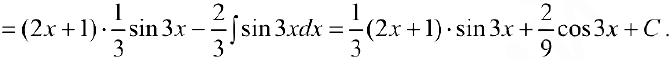
Задача №23
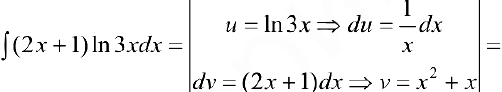
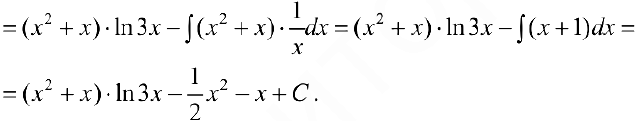
Замечание. 1. При интегрировании выражений вида:
— многочлен степени n полагают: 
После интегрирования по частям степень многочлена уменьшается на 1(см. пример 1).
2. При интегрирования выражений вида:
полагают:
(
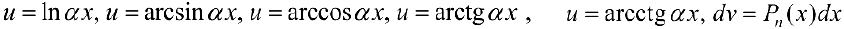
— многочлен). После интегрирования по частям интеграл упрощается (см. пример 2).
Задача №24
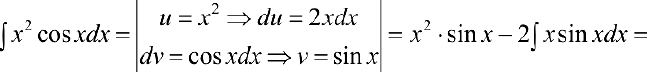
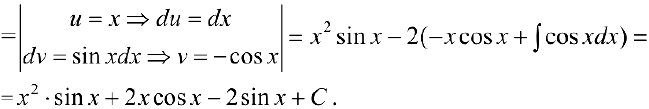
Задача №25
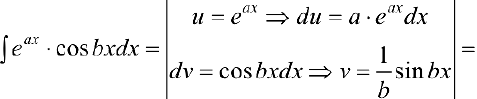
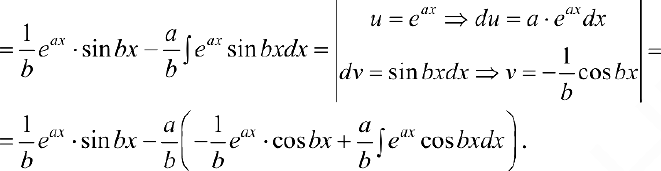
To есть 
Таким образом, проинтегрировав дважды по частям, получили уравнение, содержащее 
в правой и левой части. Решив его, получим:
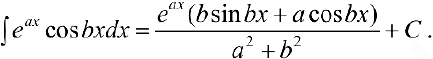
Эта теория и задачи с решением взяты со страницы готовых задач с решением по математическому анализу:
Решение задач по математическому анализу
Возможно эти темы вам будут полезны:
